黑塞矩阵(Hessian Matrix)

黑塞矩阵(Hessian Matrix)

黑塞矩阵是一个多元函数的二阶偏导数构成的方阵, 描述了函数的局部曲率.

黑塞矩阵常用语牛顿法解决优化问题, 利用黑塞矩阵可判定多元函数的极值问题. 在实际工程问题的优化设计中, 所列的目标函数往往很复杂, 为了使问题简化, 常常将目标函数在某点邻域展开成泰勒多项式来逼近原函数, 此时函数在某点泰勒展开式的矩阵形式中会设计到黑塞矩阵.

 

 

 

 

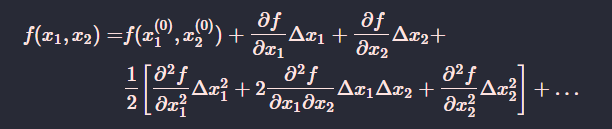
表示成矩阵形式即为

 

 

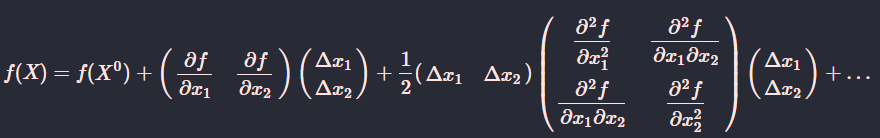
其中, 记

 

 

 

 

 

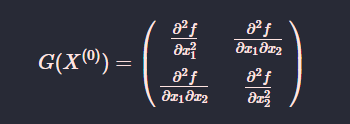
将结论扩展到多元函数:

利用黑塞矩阵判断多元函数的极值

 

 

则有

1. 当A为正定矩阵时, f在M0M0为极小值;
2. 当A为负定矩阵时, f在M0M0存在极大值;
3. 当A为不定矩阵时, M0M0不是极值点.
4. 当A为半正定矩阵或半负定矩阵时, M0M0是"可疑"极值点.