CDH、HDH、IDH、DDH、BDH、DBDH假设

 

预备知识和基本群论
素数与可除性
算数基本定理：任何大于1的整数都可由若干素数乘积获得
令α为整数， b为正整数， 贝!J存在唯一的整数q, r满足α ＝ qb + r
设α， b为正整 数， 则存在整数X, Y满足Xα ＋ Yb = gcd （α， b）
如 果c|ab伪 ， 且gcd（a， c) = 1 ， 则c|b
如果p|N, q|N， 且gcd (p， q) = 1， 则pq | N
模算术
若a ＝ qN+r，则r =a（mod N）
同余：a（mod N）=b（mod N），则称a，b同余，同余是一个等价关系（自反，对称，传递）
可逆：对于a存在a^ -1有aa^-1=a(modN)，称a和a ^-1关于N互逆
设α， N为整数， N > 1， 则当且仅当gcd (a, N）=1时α关于模N可逆。
群
定义：群是一个集合G和其上的二元运算◦， 满足下列条件：

封闭性：g, h ∈ G, g ◦ h ∈ G.
存在单位元：e ◦ g = g = g ◦ e.
存在逆元：g ◦ h = e = h ◦ g
结合律：(g1 ◦ g2) ◦ g3 = g1 ◦ (g2 ◦ g3)
交换律：g ◦ h = h ◦ g
那么当运算◦为已知时，称集合G为群。通常情况下，并不用◦来表示群运算 。根据所讨论的群的情况用加号+，或者乘号 * 来表示。 当用加法符号时， 群运算应用到两个元素g, h时表示为g + h； 单位元用 0 表示 ， 元素g的逆元素用-g表示 。当用乘法符号时，群运算应用到两个元素g, h，时表示为g· h或者简写为gh,单位元用1表示，元素g的逆元素用g^-1表示。 这并不意味着群运算对应于整数加法和整数乘法

一个集合在某种运算上可能是一个群， 但在其他运算上可能不是
实数集合R在乘法运算上不能构成群， 因为 0 没有乘法逆元
设整数 N>=2。 如 果集合｛0· · · , N - 1 ｝满足加法模N运算(也就是说α ＋b=α ＋ b (mod N))， 则此群是阶为 N的阿贝尔群，记为Z< N>
设G为群， 且α，b, c ∈ G。 如果时 ac＝bc ， 则α ＝ b. 特别地， 如果αc = c， 则α是G的单位元。
设G是一个有限群， 其阶m = lGI， 则对任意元素g ∈G， 有g^m= 1。证明：任选g∈G，令g1，g2。。。。gm为G中的所有元素，则g1g2…gm=（g1g)(g2g)…(gm*g）因为都表示了群中的所有元素，那么就有g^m= 1
----所以有个很重要的结论，在幂运算中可以通过对群的阶取模来运算
改为加法，则变成了如果g是阶为m群的一个元素 ，则 有i · g = （i modm）· g
令G是一个有限群 ，m=|G|> 1 。 令e > 0是一个整数 ， 并且定义函数fe :G→G 通过fe (g）=g^e。 如果gcd (e, m) = 1 ，则fe是一个置换
Z*< N>群
定义：

 

 

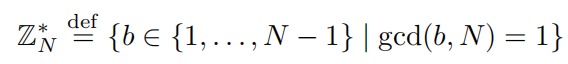
令N > 1且为整数 ， 则Z< N>在关于模N的模乘运算下为阿贝尔群
群的阶: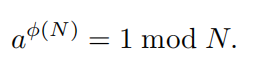

 

 

群同构与中国剩余定理
群同构定义：

 

 

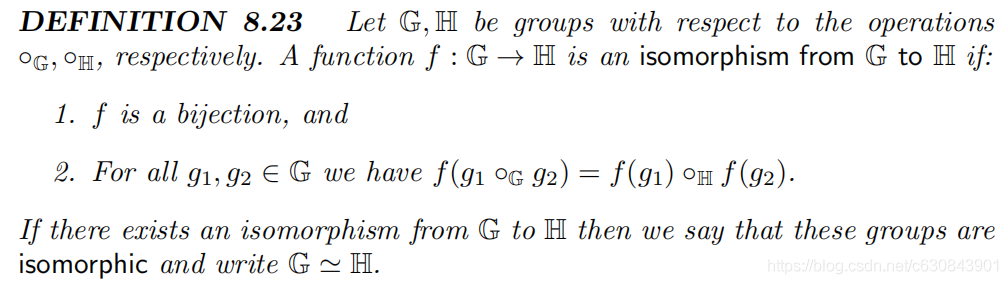
注意：若f是G到H的同构，那么函数f^-1是H到G的同构

叉乘G×H:运算后有|G|*|H|个元素

 

 

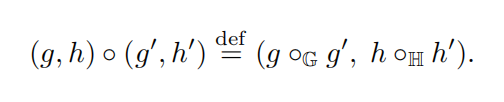
中国剩余定理：若N=pq，且p，q互素。则

 

 

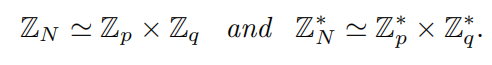
此外f为Z< N>到Z< p>×Z< q>的同构以及Z*< N>到Z*< p>×Z*< q>的同构，其中f为

 

 

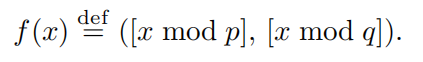
证明同构：+N为模N的加运算，田为Zp×Zq的群运算

 

 

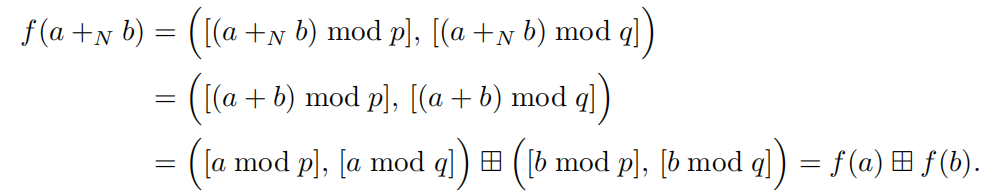
注意其中q，p只要求互素，不要求是素数，且中国剩余定理在多个分解数下仍然成立
-----中国剩余定理的应用。如果两个群同构，则代表它们有相同的“代数结构”。选择不同表示方法会影响群运算的计算效率。

元素对N取模的表示法和元素对p或q取模的表示法之间来回转换的方法：将（xp，xq）转换到x

 

 

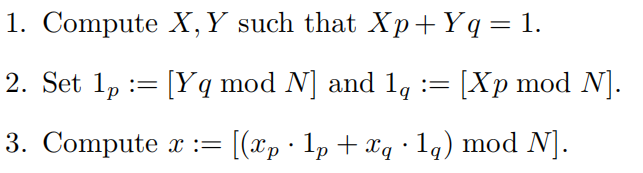
素数、 大数分解和 RSA
弱因子分解实验：

 

 

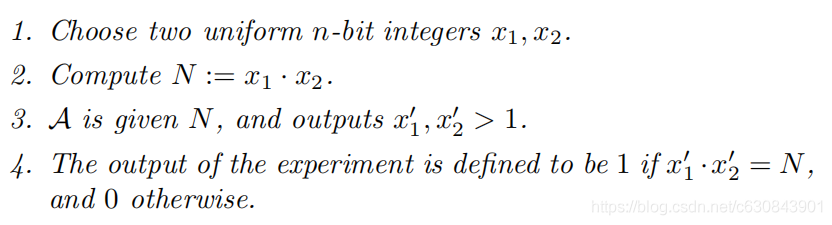
随机素数的产生
在确定范围内选取随机素数的一般方法：

 

 

注意高位拼接确定为1，变固定了输出位nbit

存在常量c，满足对任意的n > 1，n位素数的个数至少为c· 2n-1/n，（即一个n位数为素数的概率为c/n）。所以当t取n^2/c时，在算法执行t次中 仍没有素数被选中的概率为e^-n,该值是可以忽略的
素数判定
概率素数测试算法： Miller-Rabin算法：有两个输入参数，1.用于素性测试的整数p 2.一个确定错误概率的参数t
概率：

 

 

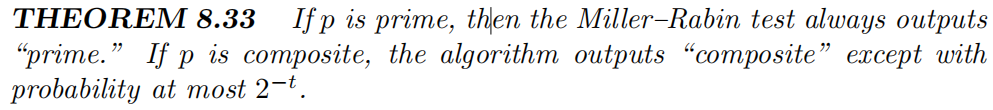
算法：

 

 

那么将Miller-Rabin算法代入随机素数生成算法中，就可以得到一个完整的生成算法
设G为有限群，且H∈G。假设H包含G的单位元，并且对于任意a, b ∈H，有ab ∈H。则H是G的一个子群。
设H为有限群G的严格子群（也就是说G≠H)。则|H|≤|G|/2。

 

 

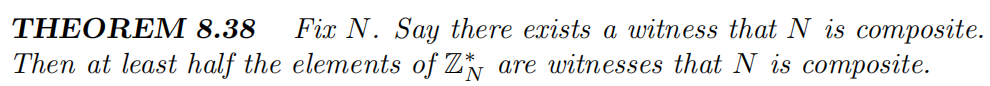
即要测试N是不是合数，如若有1个数a属于Zn，有a^N-1=1(mod N）则将它归到集合Bad中，1∈Bad，且Bad是一个严格子群，表明|Bad|≤|ZN|/2，所以ZN中至少一半元素不属于Bad。所以选定一个测试数来检验N，在任何t迭代中都没有找到证人的概率（因此算法错误输出“素数”的概率）最多为2^−t
但有例外：没有任何证据的合数N有无穷多个 ，具有此特性的N称 为 Carmichael 数
若设N-1 =u2^r，其中u为奇数且r>=1.那么a ^N-1=a ^(u2 ^r)=1(mod N),考察r+1项（a ^ u,a ^ 2u…,a ^(u*2 ^r)）.因此如果其中出现了一个1或-1，之后全是1了

 

 

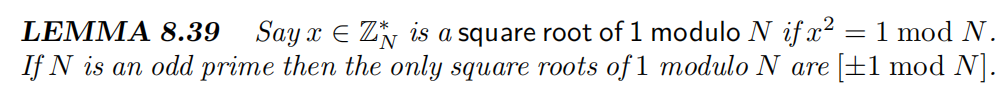
强证据：如果①a^u!=士1 mod N，且②对于所有i ∈ {1,…,r - 1}，有a ^(u*2 ^t)!=-1 mod N，则称a ∈Zn是“N为合数的强证据”

设N为奇合数，则Z*< N>中至少一半的元素为N是合数的强证据。设Bad为不是强证据集合，定义Bad’有1️⃣Bad为Bad’的子集2️⃣Bad’为Zn的严格子群，所以有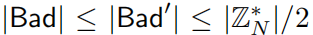

 

 

因此，Zn中至少一半的元素为强证据，其中Bad’定义为

 

 

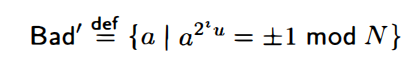
这里i表示满足a ^(u*2 ^i)=-1 mod N的最大的整数

完整的 Miller–Rabin算法

 

 

因子分解假设
设GenModulus为多项式时间算法，满足输入1"，输出(N，p ，q)，其中N= pq
实验如下：大数分解是困难的，即输出1的概率可忽略不计

 

 

RSA 假设
RSA实验：

 

 

其中的GenRSA（1^n）算法如下：

 

 

即给出pq找到（p-1）(q-1)是有难度的，RSA的困难性来源于此

关联 RSA 和分解假设
有一种概率多项式时间算法，输入一个复合整数N和整数e，d，其中ed=1modφ(N)，输出一个N因子，的概率可以忽略不计。
证明:
若N=pq，则有4个模1的平方根，其中两个为±1，还有两个其他平方根
其他平方根可用于计算q和p，因为0=y^2-1=(y-1)(y+1)modN又因为y!=±1modN所以gcd(y-1,N)=N的质因子之一
循环群中的密码学假设
循环群和生成元
设G为有限群，g∈G。g的阶为满足g^i= 1的最小整数i。
设G为有限群，g ∈G且其阶为i。则对任意整数x，有g^x= g^(x modi)。
设G为有限群，g ∈G是阶为i的元素。则当且仅当x= y mod i时，有g^x= g^y。
设G是阶为n的有限群,若元素g ∈G的阶为i，则i|m。
如 果G是一个阶为素数p的群， 则G为循环群。 此外G中的元素除单位元外都是G的生成元
离散对数和 Diffie-Hellman 假设
离散对数定义：如果G是阶为q的循环群，则存在一个生成元g∈G满足{g^ 0 g^1,…, g^(q-1)} =G。等价的，对任意h ∈G，存在唯一x ∈Z满足g^x= h。当群G已知，称x为h关于g的离散对数，记为x=log< g>h。注意，对任意整数x’，如果g^x’=h，则log< g>h =[x’mod q]。强调这种情况下的对数称为“离散”，因为值在有限范围内，相反“标准”对数是因为值的范围为无穷集合

离散对数问题：给随机h∈G作为输入，计算log< g>h,离散对数实验就是基于这之上，成功的概率可以忽略不计

计算Diffie-Hellman问题（CDH)：给定h1和h2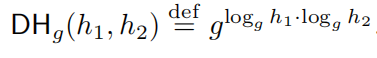

 

 

判定Diffie-Hellman问题（DDH)：给出一个h，判断h是随机选取的还是，有h=DH< g>(h1,h2),即区分｛h，h1，h2｝和｛DH< g>(h1,h2)，h1，h2｝

在Zp（的子群 ）中工作
p为素数的群Z,是一类循环群，在该群中离散对数问题被认为是困难的。具体而言，设g为一个算法，其输入为1^n，输出随机选择的一个n位素数p，群Zp的阶q=p- 1，其生成元为g。它没有素数阶并且判定Diffie - Hellman问题在这些群中并不是困难的

x∈Z,满足x^2=y mod p，则元素y ∈Z*为模p平方剩余

若p是一个强素数，即p=2q+1,q为素数，则模p的二次剩余正好有q个，又因为q是素数，所以这个二次剩余群是一个循环群，除单位元之外全是生成元（这里的2可以换做3，4。。。。）

 

 

椭圆曲线群
椭圆曲线：其中A和B满足条件4A^3 + 27B^2 = 0,（x,y）为定义在椭圆曲线上的点，O称为无穷远处

若我们从图形的角度来看

 

 

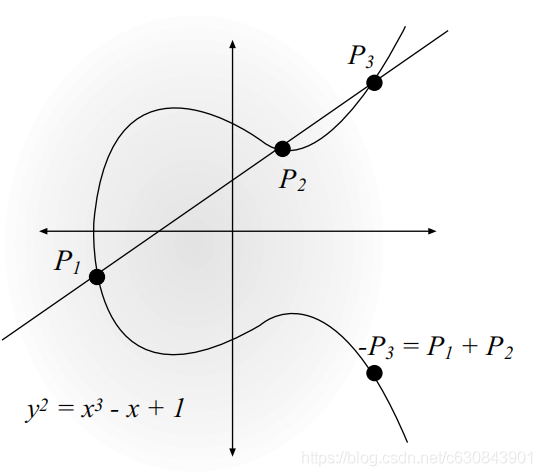
有以下结论:

如果直线和曲线在P点相切 ，则点P计算两次
无穷远处的点也要计算在内（当直线垂直时）
可以定义一个二元运算，称为 “加 ” 并用符号 “ ＋ ” 表示，有P+O = O+P = P 。和P1 + P2十P3 = O
取反：P + (-P) = 0，在图中表示为-P=（x,-y）
加法：P1,P2为曲线上任意两点，连接这两点得到一条直线，找到这条直线与曲线的第三个焦点P3然后找到此点关于x轴的对称点即为

计算两点和的方法：

 

 

点E(ZP)的集合和上面定义的加法规则形成了一个交换群，称为E的椭圆曲线群，从加法的定义方式开始，O作为恒等式，我们已经看到E(Zp)上的每个点在E(ZP)中都有一个逆

Hasse bound：这意味着在给定的椭圆曲线y^2=f(x)modp上找到一个点总是很容易的：简单地选择均匀的x∈Zp，检查f(x)是0还是二次剩余，如果是的话，令y=f(x)的平方根。

 

 

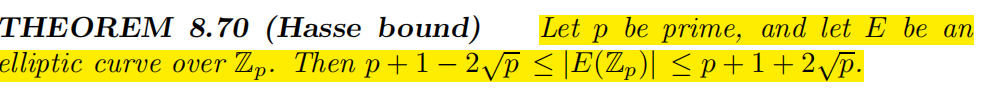
- 一种生成椭圆曲线的方法：

 

 

对于椭圆曲线的改进
点压缩：一个点所需的比特数可以减少一半，因为对于椭圆曲线E : y^2 = f(x)modp，最多有两点的x的值是一样的，即(x,y)和(x,-y),那么我们就可以set b = 0 if y < p/2and b = 1 otherwise。所以我们就可以通过x和b的值来恢复y
投影坐标： (x, y)来表示椭圆曲线上的点称为仿射坐标，那使用（X,Y,Z）来表示椭圆曲线上的点称为射影坐标，其中x=X/Z,y=Y/Z。好处：我们可以添加点，而不必计算模p的逆

 

 

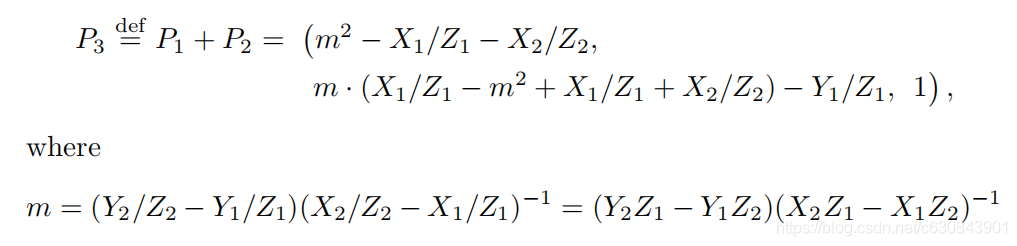
密码学应用
单向函数和置换
单向函数正式定义：如果满足下面两个条件，则函数f ∶{0,1}*→{0,1}*是“单向函数”

(容易计算)存在一个多项式时间算法，输入x，输出f (x)。
定义
(求逆困难)对任意概率多项式时间算法A，存在一个可忽略函数negl，满足Pr[Invert<A,f(n)>= 1] ≤negl(n)
使用Gen用作单向函数的函数f< Gen>:

 

 

定义：如果分解问题与Gen相关是困难的 ，则f< Gen>是一个单向函数

三元组Il = (Gen, Samp,j）如果满足下列条件 ，则其为一个函数簇z

参数产生算法Gen:输入为1^n，输出参数I，满足|l|>=n。每一个由Gen输出的I值定义了集合D< L>和R< L>，分别构成函数f 的定义域和值域。
取样算法Samp:输入为I，输出一个均匀分布的集合D< L>中的元素
确定性评估算法f:输入为I，x ∈ D< L>，输出一个元素y ∈ R。记为y = f< l>(x)。ll是一个置换簇:如果对Gen(1")输出的I的每个值，满足D< L>=R< L>且函数f < L>:D< L> →R< L>为双射。
反转实验：

 

 

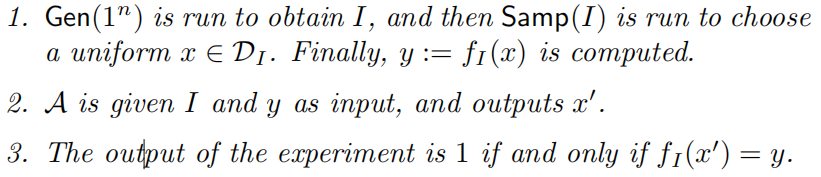
所以若RSA如果RSA问题对GenRSA而言是困难的，则此函数簇实际上为单向函数
使用离散对数的思想构造单向函数：

 

 

构造抗碰撞的散列函数
现在介绍一个基于素数阶群离散对数假设构造的抗碰撞散列函数

设G为多项式时间算法:输入1^n，输出一个循环群G，其阶为q(|q|=n)，和一个生成元g。定义一个定长散列函数如下:

 

 

需要注意的是：

Hs以Zq×Zq作为输入。可视为将长度为 2(n 一1)的比特串作为输入。原因是输入x ∈ {0,1}^2(n-1)可拆分成两个串x1, x2，且每个长度为n -1
输出固定为G中元素，意识有可能需要填充
当G中元素可以用少于2^n－2位表示的时候才可使用
如果离散对数问题与G相关是困难的， 则上面的构造方法是一个定长抗碰撞散列函数，证明方法如下（将碰撞的困难规约到离散对数分解的困难）：若有方法使其碰撞，那么离散对数问题也就解决了

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

————————————————
版权声明：本文为CSDN博主「Famidlistimo」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_44029550/article/details/111387705