Visual Stdio 2019 中编译调用miracl库实现双线性配对
前言
最近实现密码算法,需要使用到椭圆曲线加密、双线性配对等数学工具,只会些C++,故选择调用miracl大数库。在啃了好几天的github上的源码后,才对它有所了解。写下此篇博客,希望后来研究者可以少走弯路~~
1.前期准备
(1)miracl函数库lib生成
https://miracl.com/miracl/(函数库下载网址)
在使用miracl大数库之前需要配置环境,我使用的开发软件是VS2019版本,语言C++
lib的配置参照此博主,写的很详细,不再赘述:https://blog.csdn.net/qq_36290650/article/details/83421230?spm=1001.2014.3001.5501
不过最后该博客认为源文件必须改成.c后缀,我使用cpp后缀也是可以的
(2)双线性配对的介绍和调用
miracl库里有两种默认的配对,一型和三型配对,前者使用eta_T配对(在有限域GF(2^m)上)和Tate配对(在有限域GF(p)上),后者使用最优ate配对。一型配对使用pairing_1.h声明,ssp_pair.cpp实现,三型配对使用pairing_3.h声明,ss2_pair.cpp实现(所述的文件皆在源码中pairing目录下)。配对实现基于四种安全等级:AES_80、AES_128、AES_192和AES_256,一型配对仅支持前两种。关于选择哪种配对更好,说明文件给出了解释。这里,我选择了安全等级128的一型eta_T配对,配置和实现都将基于一型配对。
打开一型配对声明文件pairing_1.h,G1、GT数据类型如下所示
一型配对模式是GT=e(G1,G1),选择eta_T配对时,在源文件定义#define MR_PAIRING_SSP;选择Tate配对时,在源文件定义#define MR_PAIRING_SS2

我们继续查看ecn.h和zzn2.h,发现ecn.h还包含了一个big.h的头文件,zzn2.h包含一个zzn.h。

到此我们可以确定想要调用一型eta_T配对,需要的文件有
pairing_1.h
ssp_pairing.cpp
zzn.h
zzn.cpp
zzn2.h
zzn2.cpp
ecn.h
ecn2.cpp
big.h
big.cpp
以及1中所需要的mirdef.h、miracl.h和两个资源文件lib、pdb
现在开始写项目啦~>0<
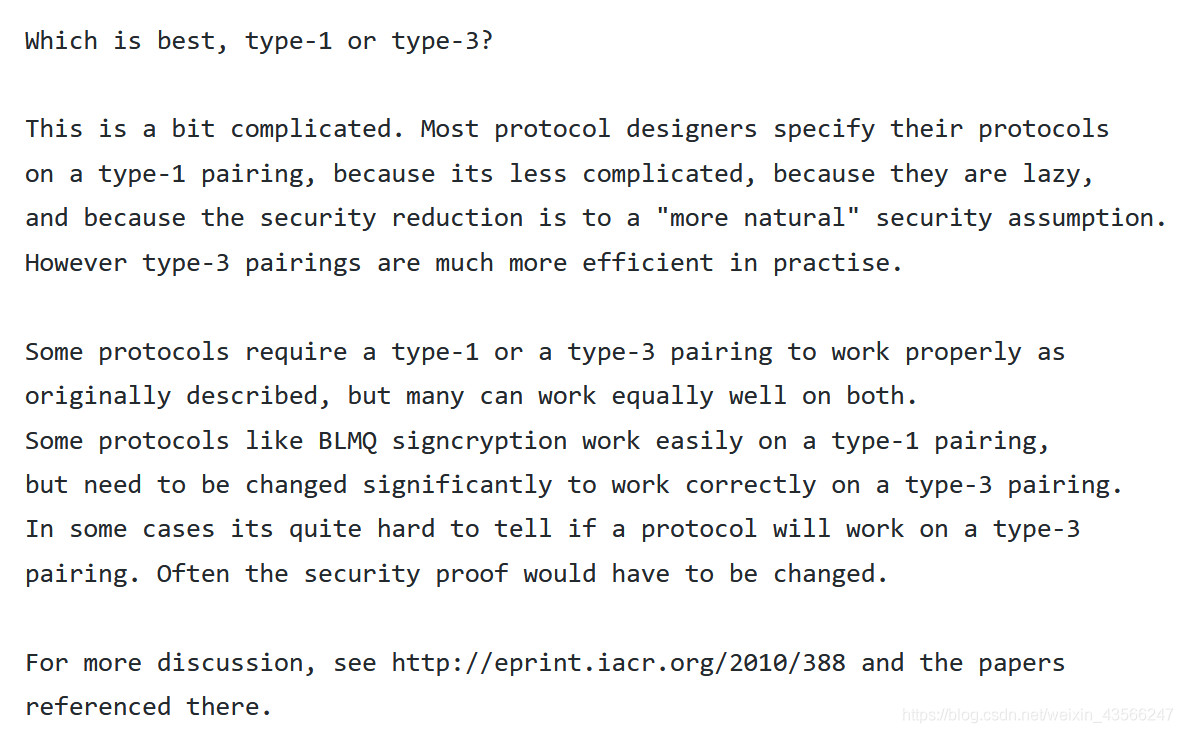
新建VS空项目,将上面所述的文件复制到项目目录下
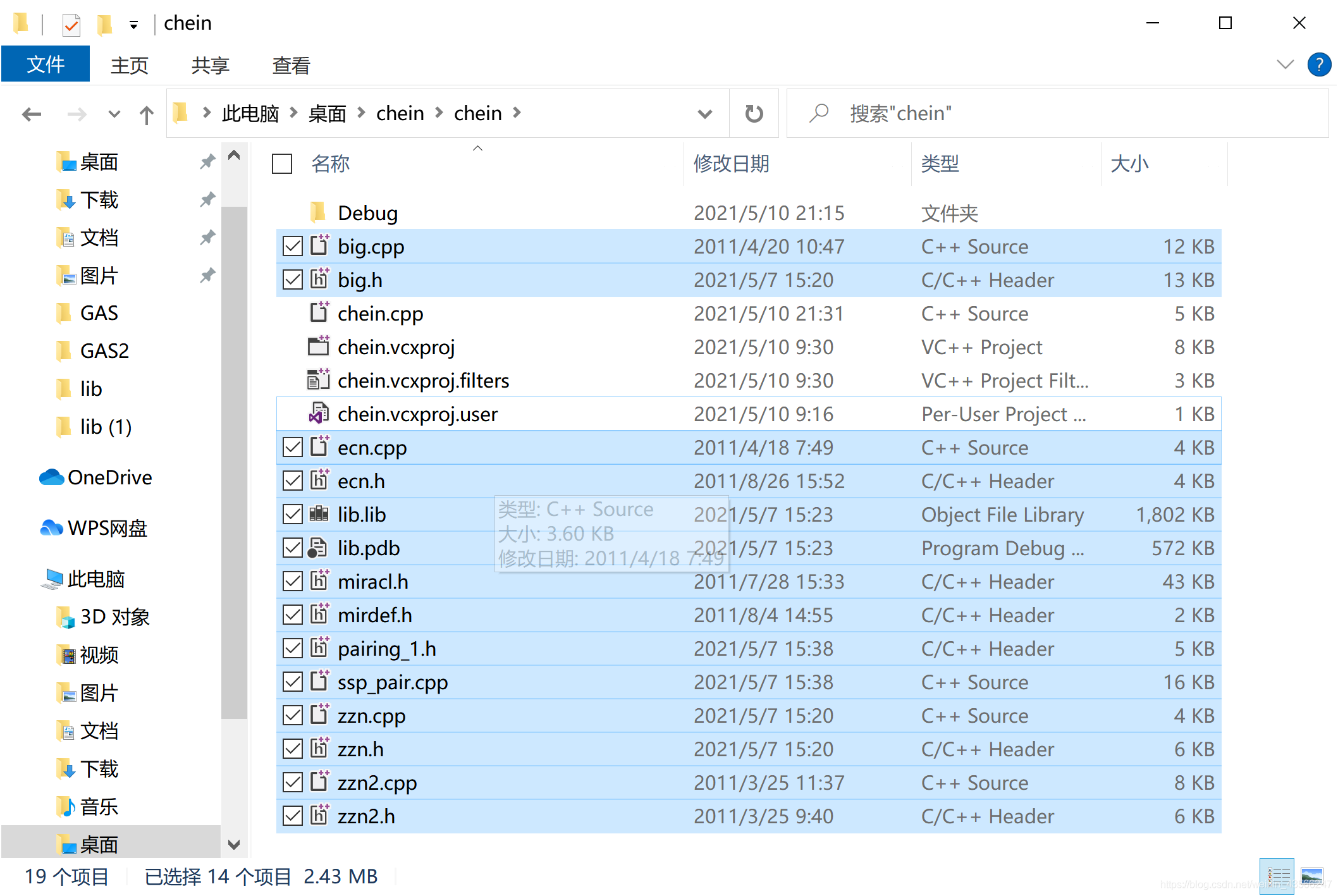
右键项目,添加现有项,添加这些文件
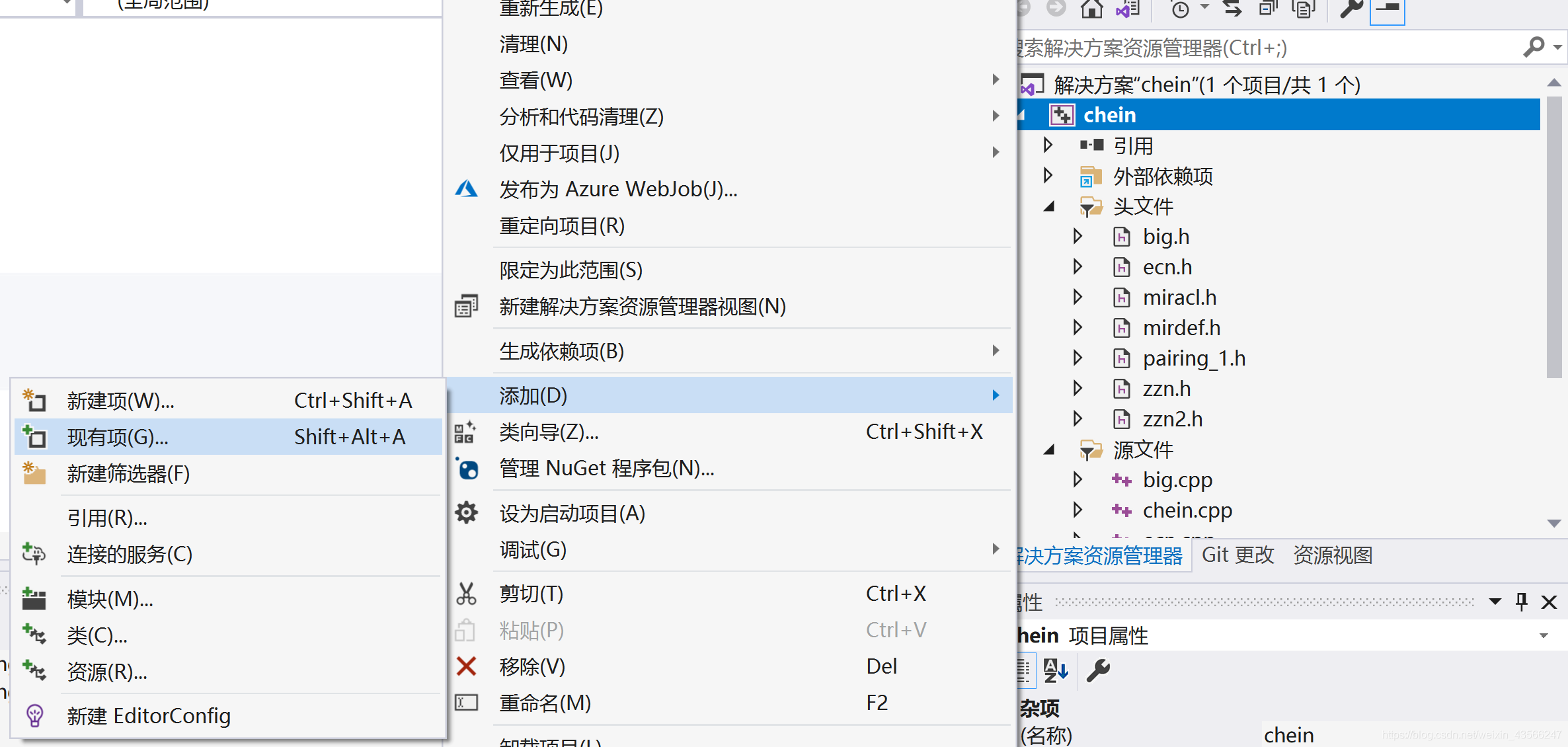
右键重新生成,这里会有一些报错,是由于源码的编写方式不标准导致的,比如说类中的友元函数无法在声明的时候添加默认参数,所以删掉false
其他的问题就不详细描述,只要稍微修改就可

然后右键添加空项目(.cpp),加上头文件
#include <iostream>
//security define
#define AES_SECURITY 128
#define MR_PAIRING_SSP
#include "pairing_1.h"
using namespace std;
extern "C"
{
#include "miracl.h"
#include "mirdef.h"
}
int main()
{
}
我所用的语言是C++,但是两个大数库的头要用C编译,右键重新生成,编译成功。(撒花~~)
2、相关源码
(1)Big类
big.h定义了Big类,Big数据类型相当于对big数据类型的进一步扩充
Big a;//定义一个Big类型变量,默认初始化为0
Big对运算符进行了重载,支持加减乘除等基本运算操作

Big类中常用函数:
a. 乘法取模
定义:Big modmult(const Big&,const Big&,const Big&);
Big a,b,c,m;
c=modmult(a,b,m); //c=(a*b)modm
b. 除法取模
定义:Big moddiv(const Big&,const Big&,const Big&);
Big a,b,c,m;
c=moddiv(a,b,m); //c=(a/b)modm
c. 幂次方函数
定义:Big pow(const Big&, int, const Big&); // x^m mod n
Big pow(int, const Big&, const Big&); // x^m mod n
Big pow(const Big&, const Big&, const Big&); // x^m mod n
Big a,b,c,m;
c=pow(a,b,m); //c=(a^b)modm
d. 随机数生成
定义:Big rand(const Big&); //0 < rand < parameter
Big a,b;
a=rand(b); // 0ab
(2)G1类、GT类
pairing.h声明了G1和GT类
不同的配对方式G1和G2表现为不同的数据类型,eta_T配对中,G1的数据类型是ecn,GT的数据类型是zzn2
G1、GT类对运算符进行了重载,支持如下运算操作

(3)PFC类
pairing.h声明了PFC(pairing friendly curve)类
PFC类中声明了双线性配对友好的椭圆曲线的参数以及相关运算函数
s=安全系数 ord[0]=椭圆曲线的阶

ssp_pairing.cpp初始化椭圆曲线以及定义了PFC类中的函数

PFC类中常用函数:(使用前先建立类对象,如PFC pfc(128);)
a. G1点乘
定义:G1 mult(const G1&,const Big&)
Big a; G1 P,Q;
Q=pfc.mult(P,a); //Q=aP
b. GT幂次运算
定义:GT power(const GT&,const Big&);
Big a; GT P,Q;
Q=pfc.power(P,a); //Q=a^P
c. 字符串哈希转换为G1点
定义:Big PFC::hash_to_group(char *ID)
G1 b=pfc.hash_to_group((char *)"Robert");
d. 随机生成AES密钥
定义:void PFC::rankey(Big& k)
Big a;
pfc.rankey(a);
e. 双线性配对
定义:GT PFC::pairing(const G1& x,const G1& y)
G1 P,Q;GT Z;
Z=pfc.pairing(P,Q); //Z=e(P,Q);
(待续~~~)
本博客文章为博主学习笔记,针对博主需要所写,内容可能不够完善或者有误,欢迎各位批评指正~转载请说明博客来处>3<
————————————————
版权声明:本文为CSDN博主「书仪」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_43566247/article/details/116642210


