IND-CPA,IND-CCA1,IND-CCA2,EUF-CMA
评估密码系统安全性主要有三种方法:
(1)无条件安全性
这种评价方法考虑的是假定攻击者拥有无限的计算资源,但仍然无法破译该密码系统。
(2)计算安全性
这种方法是指使用目前最好的方法攻破它所需要的计算远远超出攻击者的计算资源水平,则可以定义这个密码体制是安全的。
(3)可证明安全性
这种方法是将密码系统的安全性归结为某个经过深入研究的数学难题(如大整数素因子分解、计算离散对数等),数学难题被证明求解困难。这种评估方法存在的问题是它只说明了这个密码方法的安全性与某个困难问题相关,没有完全证明问题本身的安全性,并给出它们的等价性证明。
实际安全性
对于实际应用中的密码系统而言,由于至少存在一种破译方法,即强力攻击法,因此都不能满足无条件安全性,只提供计算安全性。密码系统要达到实际安全性,就要满足以下准则:
(1)破译该密码系统的实际计算量(包括计算时间或费用)十分巨大,以致于在实际上是无法实现的。
(2)破译该密码系统所需要的计算时间超过被加密信息有用的生命周期。例如,战争中发起战斗攻击的作战命令只需要在战斗打响前需要保密;重要新闻消息在公开报道前需要保密的时间往往也只有几个小时。
(3)破译该密码系统的费用超过被加密信息本身的价值。
如果一个密码系统能够满足以上准则之一,就可以认为是满足实际安全性的。
可证明安全性
3.1 可证明安全性体系的三大要素
在可证明安全体系中,有三大要素:安全模型,安全性定义和困难性问题。
安全模型分为安全目标和敌手能力。安全目标描述了安全模型要达到什么程度的安全,例如,对于加密算法的不可区分性(Indistinguishablity 简称 IND)、对于签名算法的存在性不可伪造(Existable Unforgeble 简称 EU)等。
其中不可区分性(IND)也称为语义安全(Semantic scurity),其定义如下。敌手即使获得了密文,也不能得到其对应明文的任何信息,哪怕是 1bit 的信息。其形式化的表示方法为:已知 m0,m1以及 Cb=Enc(pk,mb),其中 m0是 m0或 m1中的任意一个,即 Cb是 m0、m1其中之一的密文,敌手无法有效判断加密过程中 b 到底是 0 还是 1。
3.2 安全性定义
刻画敌手的能力,主要有四类,选择明文攻击(Chosen Plaintext Attacke 简称 CPA)、选择密文攻击(Chosen Ciphertext Attack 简称 CCA)、惟密文攻击(Ciphertext-Only Attack)、已知明文攻击(Known Plaintext Attack)。常用的刻画敌手能力是前面两类,选择明文攻击(CPA)是指由敌手选择明文并且可以得到对应的密文。选择密文攻击(CCA)是指敌手不仅可以选择明文获得密文,还能选择有限次的密文,获得对应的明文。CCA比 CPA 描述敌手的能力更强。
CPA 安全。我们把选择明文攻击(CPA)描述成一个游戏以方便我们更好的理解。首先声明一点,这个游戏的目的是在选择明文攻击的前提下攻破系统的不可区分性(Indistinguishablity),所以下面简称这个游戏为 IND-CPA。其次,还要定义两个角色挑战者 C 和敌手 A。挑战者(challenger)的任务相当裁判,主持游戏并且对敌手的行为进行反馈。敌手顾名思义,就是去攻击当前系统,而且对于这个游戏来说是采用选择明文攻击的方法进行攻击。游戏的描述如下:
A. 初始化:挑战者 C 创建 IND-CPA 系统,并且将公钥发送给敌手 A。
B. 敌手 A 选择两个长度相同的明文 m0,m1发送给挑战者 C。挑战者 C 随机选择 b∈{0,1},并将 mb加密记作 cb,然后将密文cb发送给敌手 A。
C. 敌手 A 猜测挑战者 C 上一步进行加密的明文是 m0还是 m1,并且将猜测结果输出,输出结果记为 b‘。若 b‘=b,那么敌手攻击成功。
敌手攻击的优势可以定义为如下函数:
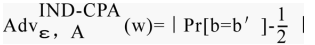
其中 w 是加密方案密钥的长度。因为随机猜测就有 1/2 的概率赢得 IND-CPA 游戏。所以
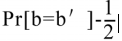
才是敌手经过努力得到的优势。如果对任何多项式时间的敌手 A,存在一个可忽略的优势σ,使得
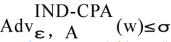
那么就称这个加密算法在选择明文攻击下具有不可区分性,或者称为 IND-CPA 安全。
CPA(选择明文攻击)
敌手可以访问到加密预言机
敌手选择明文并且可以得到对应的密文

CCA(选择密文攻击)
敌手可以访问到加密和解密预言机
敌手不仅可以选择明文获得密文,还能选择有限次的密文,获得对应的明文

CCA-1和CCA-2
CCA2 与 CCA1 只有一个区别,那就是在生成挑战密文后,CCA2依然允许敌手进行解密询问(限制是不能允许敌手询问挑战密文的解密询问)
翻译自:
https://crypto.stackexchange.com/questions/26689/easy-explanation-of-ind-security-notions
理想的加密方案E EE 是这样的,对每一个密文C = E ( K , M ) C=E(K,M)C=E(K,M).如果对于对手来说,密钥是不可见的,那么区分M MM 的概率是可忽略不计的。由于这在实践中是不可能的,第二个最合理的方式是定义足够强的限制来满足一些安全的定义。IND-notation 根据一些攻击游戏提供了这样的定义,在游戏中,挑战者保持它的密钥,对手有一定的能力并且对手的目标是破坏整个加密系统。
通常来说,一个加密系统将会有密钥生成算法K G KGKG,这将会生成一个密钥对K E , K D K_E,K_DKE,KD,(用来加密的密钥和用来解密的密钥),还有一个加密算法和一个解密算法。
-
IND-CPA INDistinguishability under Chosen Plaintext Attack 选择明文攻击下的不可区分性。
总的来说:对手生成两个相同长度的明文信息,挑战者随机地决定加密其中一个,对手尝试去猜测哪个信息被加密了。
算法:
- 挑战者:K E , K D = K G K_E,K_D=KGKE,KD=KG(安全参数)
- 对手:m 0 , m 1 m_0,m_1m0,m1= 选择两个相同长度的明文。发送m 0 , m 1 m_0,m_1m0,m1给挑战者。在多项式时间内执行 额外的操作包括调用加密oracle
- 挑战者:b bb=随机选择0或者1
- 挑战者:C : = E ( K E , m b ) C:=E(K_E,m_b)C:=E(KE,mb) 发送C给对手
- 对手:在多项式时间内执行额外的操作,包括对加密oracle的调用。输出猜测g u e s s guessguess
- 如果g u e s s = b guess=bguess=b 对手赢
在这个场景中,主要引入的概念是多项式界。现在,我们对密码的期望被减弱:从“赢得概率是可忽略不计的”,到“在一个合理的时间片中赢得概率是可忽略不计的”。对相同长度明文的限制是为了防止对手只是对比密文长度就能赢。然而,这种要求太弱,特别是因为它假设在对手和挑战者之间只有单一的交互。
-
IND-CCA1: INDistinguishability under Chosen Ciphertext Attack
总的来说:游戏的目标和IND-CPA是一样的。对手有额外的能力:调用一个加密或者解密oracle。这意味着,对手可以在得到挑战密文之前加密或者解密任意信息。基于IND-CPA游戏的基础之上,引入了对敌手A的解密帮助
-
互动的流程如下:
1. 难题挑战者首先生成难题的参数并发送给难题敌手,难题敌手伪装成算法挑战者,根据数学难题参数进一步构造算法的公钥参数并发送给算法敌手;
2. 算法敌手发起询问,这个询问根据不同的安全级别(选择明文攻击/选择密文攻击)包括密钥生成询问、加密询问或解密询问,包括难题敌手采用某些设计好的诡计返回询问结果,这些询问结果可能是真实的,可能是随机,但算法敌手绝对分辨不出来;
3. 算法敌手发起挑战,发送两段等长的明文给难题敌手,难题敌手随机选择其中一段明文,进行加密并返回给算法敌手;
4. (可选,如果是针对自适应的攻击就加上这个过程)算法敌手再次发起询问,询问内容和之前一样;
5. 算法敌手猜测密文加密的明文是哪一个,或者直接计算出明文是什么,随后难题敌手利用算法的结果做出难题的解答,并最终返回给难题挑战者。
————————————————
版权声明:本文为CSDN博主「辣油小馄饨」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/MichaelJava/article/details/78112902 -
算法:
- 挑战者:K E , K D = K G K_E,K_D=KGKE,KD=KG(安全参数)
- 对手(多项式有界的次数):对任意明文或者密文分别调用加密或者解密oracle
- 对手:m 0 , m 1 m_0,m_1m0,m1= 选择两个相同长度的明文。发送m 0 , m 1 m_0,m_1m0,m1给挑战者。在多项式时间内执行 额外的操作包括调用加密oracle
- 挑战者:b bb=随机选择0或者1
- 挑战者:C : = E ( K E , m b ) C:=E(K_E,m_b)C:=E(KE,mb) 发送C给对手
- 对手:在多项式时间内执行额外的操作。输出猜测g u e s s guessguess
- 如果g u e s s = b guess=bguess=b 对手赢
IND-CCA1考虑了重复交互的可能性,这意味着安全不会随着时间的推移而减弱。
- CCA1是午餐攻击模型,因为午餐持续的时间短,所以敌手A没有足够的时间准备他需要提问的密文,当然这里准备的密文,攻击者肯定是要想办法构造与目标密文相关的密文,使得通过解密预言机之后可以得到与目标密文对应明文相关的明文。因此午餐时间敌手A提问的所有的密文都是午餐前准备的。
- 午餐攻击是一个非常受限的攻击模型,敌手A只能在很短的时间内获得提供给他的解密服务,就好像“午餐”以后解密盒被永久的关闭一样。
-
IND-CCA2: INDistinguishability under adaptive Chosen Ciphertext Attack
总的来说:除了IND-CCA1的能力以外,对手在收到C CC后可以访问oracle,但是不可以发送C CC给解密oracle。
- 在IND-CCA1的基础上,去掉了只能在短时间内得到解密帮助这个不现实的条件,即在这个更强安全性的攻击模型中,对敌手A的解密帮助在午餐攻击前后都可以得到,我们去一个“美丽的”名字------凌晨攻击。
-
算法:
- 挑战者:K E , K D = K G K_E,K_D=KGKE,KD=KG(安全参数)
- 对手(多项式有界的次数):对任意明文或者密文分别调用加密或者解密oracle
- 对手:m 0 , m 1 m_0,m_1m0,m1= 选择两个相同长度的明文。发送m 0 , m 1 m_0,m_1m0,m1给挑战者。在多项式时间内执行 额外的操作包括调用加密oracle
- 挑战者:b bb=随机选择0或者1
- 挑战者:C : = E ( K E , m b ) C:=E(K_E,m_b)C:=E(KE,mb) 发送C给对手
- 对手:在多项式时间内执行额外的操作,包括对不同于C CC的密文的oracle的调用。输出猜测g u e s s guessguess
- 如果g u e s s = b guess=bguess=b 对手赢
IND-CCA2建议,在了解密文之后使用解密oracle在某些方案中具有合理的优势,因为可以根据特定的密文定制对oracle的请求.
-
如果一个密码系统能抵抗适应性选择密文攻击,那么他则可以抵抗其余几种攻击(非适应性选择密文攻击、适应性选择明文攻击、非适应性选择明文攻击、已知明文攻击、唯密文攻击)。
目前普遍认为,任何新提出的公钥加密算法都应该在适应性选择密文攻击下达到语义安全性,即IND-CCA2。
-
3.3 困难问题
有了安全模型和安全性定义,通常使用规约到困难问题的方法来进行安全性证明。密码学中常用的困难问题有离散对数困难问题(discrete logarithm problem,简称 DLP)、CDH 问题(Computational Diffie-Hellman) 、DDH 问题(Decisional Diffie-Hellman)以及 BDH 问题(Bilinear Diffie-Hellman)。
3.4 可证明安全性理论
有了前面叙述了安全模型,安全性定义,困难性问题,可证有了前面叙述了安全模型,安全性定义,困难性问题,可证明安全体系也变得可行。可证明安全性是指利用“规约”的方法,将攻击密码算法或安全协议的方法规约到一个攻击困难问题上。首先确定加密体制的安全目标,如签名体制的安全目标是签名的不可伪造性(Existable Unforgeble),加密体制的安全目标是信息的不可区分性(Indistinguishablity)。然后根据安全性定义确定敌手的能力构建一个安全性模型。
规约是复杂性理论中的概念, 一个问题P1规约到问题P2是指,已知解决问题 P1的算法 M1,我们能构造另一算法 M2,M2可以以 M1作为子程序,用来解决问题 P2。
将规约的方法应用在密码算法或安全协议的安全性证明上,例如,可以将敌手对密码算法或安全协议(P1)的攻击规约到一些已经得到深入研究的困难问题(P2)。即若敌手能够对算法或协议发起有效的攻击,就可以利用敌手构建一个算法来攻破困难问题,然而困难问题是已经被证明无法攻破的,这样就出现矛盾。根据反证法,敌手可以攻破算法或协议假设不成立,证明完毕。
一般来说,为了证明方案 1 的安全性,我们可以将方案 1 规约到方案 2,即如果敌手 A 可以攻破方案 1,那么敌手 B 同样也可以攻击方案 2,而方案 2 已经被证明是安全的,或者是一个难题。
证明过程通过一个思维游戏来描述。首先,挑战者创建方案2,B 表示方案 2 中的敌手,A 表示方案 1 中的敌手。B 为了攻破方案 2,利用 A 作为子程序来攻击方案 1。B 想要利用 A,就需要对 A 进行训练,所以 B 模拟了 A 的挑战者。
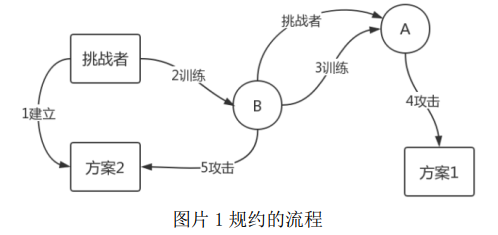
例如,如果要对加密算法进行安全性证明,那么方案 1 就是具 体 的 加 密 算 法 。 假 设 安 全 目 标 是 信 息 的 不 可 区 分 性(Indistinguishablity),敌手 A 的能力是可以选择明文攻击,即 CPA。敌手 B 模拟敌手 A 的挑战者,与 A 进行 IND-CPA 游戏。在游戏过程中,B 为了实现自己的目的利用 A。如果 A 无法判断自己是与 B 还是与挑战者做游戏,那么称 B 的模拟是完备的。
对于其他加密算法或加密协议,我们必须首先确定它想要实现的安全目标,例如签名方案的不可伪造性,然后根据安全性定义确定敌手的能力构建一个安全性模型,再把对加密算法或加密协议的攻击规约到已被证明的困难问题上。 这就是可证明安全性。
结语:可证明安全性理论是密码学理论与计算复杂性理论的一次完美结合,也是现代密码学的基石。在过去的 30 年终,现代密码学最大的突破就是把密码学体系建立在计算复杂理论上,这使得密码学从一门艺术发展成为一门严谨的学科。
-
签名体制的语义安全性(EUF-CMA)
对于数字签名体制,存在以下几种伪造类型完全攻破:攻击者能够产生与私钥持有者相同的签名,这相当于恢复出了私钥
选择性伪造:攻击者能够伪造一个他选择的消息签名
存在性伪造:攻击者能够伪造一个消息的签名,这个消息可能仅仅是一个随机比特串
签名体制的语义安全性,由不可伪造(Existential Unforgeability)游戏(简称EUF游戏)来刻画
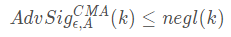
————————————————
版权声明:本文为CSDN博主「hhh_2333」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_36291381/article/details/106805123


