可证明安全

在 ROM 中证明了的方案安全并不能保障该方案在现实生活中的安全性。目前，存在许多 ROM 中是可证安全的，但具体的应用中却无法构造出相应的实例。标准模型中可证安全更具有重要的现实意义。在标准模型中，算法仍然是通过预言机来弥补对私钥的无知，不同在于这个预言机的内部映射并不是随机指定的，必须符合具体方案中的函数关系，这样增加了方案设计的难度。尽管 ROM 方法论并不能作为实际方案安全的绝对证据，但其可作为任何实际方案的一种必要的基本安全测试，ROM 方法论至少可以排除很多安全隐患。利用 ROM 设计简单而有效的协议，可以抵抗许多未知攻击。也有一些学者仍然坚持在标准模型中证明方案安全性，认为尽管在 ROM 中可证安全的方案非常有效，但是把哈希函数看成了一个完全随机的理想模型，这是一种很强的假设，而且方案在 ROM 中的安全性和通过哈希函数实现的安全性之间无必然的因果关系。例如，一些签名和加密方案在 ROM 中是安全的，但在实际应用中却不是安全的。
————————————————
版权声明：本文为CSDN博主「谨墨」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43137080/article/details/109595044

 

现代密码学中的安全标准有3个:
(1) 计算安全: 考虑攻破一个密码算法所需的计算开销. 若攻破一个密码算法的最优算法所做操作是n次, 则称该密码算法是计算安全的. 但实际上没有一个实例属于计算安全, 目前仅是一个理论概念.

(2) 可证明安全: 基本思想基于数学中的反证法, 通过"规约"的方式将密码算法安全性规约到某个公认的数学难题, 比如大数分解, 素数域离散对数分解问题. 若存在攻破密码算法的攻击方式, 则可以利用该方式构造出攻破数学难题的方法.
实现一个密码算法的可证明安全, 大致步骤有

给出密码算法的形式化定义
给出密码算法的安全目标
给出密码算法的安全模型, 包括攻击者的目标和攻击者的攻击能力
对攻击者的攻击过程进行规约, 利用攻击方法解决数学难题
(3) 无条件安全: 假设攻击者拥有无限计算能力, 无限计算资源, 仍然不能攻破密码算法, 则密码算法是无条件安全的. 显然这是一种理想化的概念, 实际中基本不存在.

安全模型
可证明安全中需要证明攻击者采取最强的攻击能力, 依然不能实现最弱的攻击目标, 则称密码算法是可证明安全的.

安全目标
主要分为3类
(1) 不可区分性 (IND)

 

 

(2) 非延展性安全 (NM)
得到明文M对应的密文C, 要求攻击者 A \mathcal{A} A无法构造不同的密文C’, 使C’对应的明文M’和M存在某种关联, 且 A \mathcal{A} A可以得知这种关联关系.

(3) 单向安全性 (OW)
要求公钥密码方案实现单向安全性, 即攻击者从公开参数不能解密密文.

小结:
通常OW要求比IND和NM低, NM的安全性证明最困难, 所以大部分安全性证明是基于IND.

攻击能力
攻击者的攻击能力分为4类
(1) 唯密文攻击 (COA)
攻击者只知道密文.

(2) 已知明文攻击 (KPA)
攻击者知道一些明文-密文对

(3) 选择明文攻击 (CPA)
攻击者可以选择特定明文-密文对, 如果还可以在攻击过程中, 调整明文选择, 且得到对应密文, 称为适应性CPA.

(4) 选择密文攻击 (CCA)
攻击者可以选择特定密文-明文对, 如果还可以在攻击过程中, 调整密文选择, 且得到对应明文, 称为适应性CCA. 普通CCA称为CCA1, 适应性CCA称为CCA2.

总结
同时考虑安全目标和攻击能力两个方面, 主要的安全组合有6类

IND-CPA
IND-CCA1
IND-CCA2
NM-CPA
NM-CCA1
NM-CCA2
IND-CCA2, NM-CCA2安全性最强. IND-CPA又称为语义安全, 主要的CP-ABE问题都是基于IND-CPA安全. 另外IND-CPA下安全方案有某种通用方法转换为IND-CCA.
————————————————
版权声明：本文为CSDN博主「fa1c4」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_33976344/article/details/116377007

 

 

语义安全
语义安全表示为攻击者即使已知某个消息的密文，也得不出该消息的任何部分信息，即使是1比特的信息

​在完美保密性中，对于等长的消息m，m属于可被该加密算法加密的消息空间，当m用密钥k加密后，加密结果无法得到m的任何信息。形式化的定义为如下：

 

 

 

​目前能够到达这个安全条件的加密算法只有一次一密（One-time Pad），由于加密使用的密钥长度至少需要同消息长度相同，因此一次一密在实践中没有应用价值。

​在实际的加密算法中，只需要保证实际保密性就行。目前按照图灵机的定义，计算机最多能计算多项式时间（Polynomial Time）内能解决的问题，最多有多项式大的存储空间（Polynomial Storage）。实际保密性就是计算机无法从加密结果中得到有关明文的任何信息。形式化定义如下：

 

 

 

 

不可区分性游戏
加密方案语义安全的概念由不可区分性(Indistinguishability) 游戏，简称IND游戏来刻画，这种游戏是一种思维实验。其中有2个参与者，一个称为挑战者（challenger)，另一个是攻击者（attacker）。挑战者建立系统，攻击者对系统发起挑战，挑战者接受攻击者的挑战。

公钥加密方案在选择明文攻击下的不可区分性(IND-CPA)
初始化：挑战者产生系统E，攻击者获得系统的公开钥
挑战：攻击者输出两个长度相同的消息m0和m1。挑战者随机选择b ∈ \in ∈{ 0,1}，将mb加密，并将密文给攻击者
猜测：攻击者输出b’，如果b’ = b, 则攻击者攻击成功
攻击者的优势可定义为参数k的函数：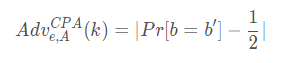

 

 

 ​其中k是安全参数，用来确定加密方案密钥的长度。因为任一个不作为的攻击者A，都能通过对b做随机猜测，而以1/2的概率赢得IND-CPA游戏。而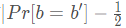 

是攻击者通过努力得到的，故称为攻击者的优势。如果攻击者A式多项式时间，而它的优势可忽略不计，即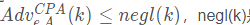

 

 

 是一个可忽略函数。此时这个加密算法在选择明文攻击下具有不可区分性（IND-CPA安全）如果加密方案是确定的，如RSA算法、Rabin密码体制等，每个明文对应的密文只有一个，敌手只需重新对 m 0和 m 1 加密后，与目标密文进行比较，即赢得游戏。因此语义安全性不适用于确定性的加密方案。与确定性加密方案相对的是概率性的加密方案，在每次加密时，首先选择一个随机数，再生成密文。因此同一明文在不同的加密中得到的密文不同，如ElGamal加密算法。

公钥加密方案在选择密文攻击下的不可区分性(IND-CCA)
IND-CPA安全仅仅保证攻击者是完全被动情况时（即仅做监听）的安全，不能保证攻击者是主动情况时（例如向网络中注入消息）的安全。非适应性选择密文攻击（Chosen Ciphertext Attack，CCA）描述了攻击者的主动攻击。攻击者在获得目标密文以前，可以访问解密谕言机(Oracle)。谕言机获得目标密文后，希望获得目标密文对应的明文的部分信息。

初始化：挑战者产生系统E，攻击者A获得系统的公开钥
训练：攻击者向挑战者（或解密谕言机）做解密询问（可多次），即取密文c给挑战者，挑战者解密后，将明文给攻击者
挑战：攻击者输出两个长度相同的消息m0和m1，再从挑战者接收mb的密文，其中随机值b ∈ \in ∈{ 0,1}
猜测：攻击者输出b’，如果b’ = b, 则攻击者攻击成功
公钥加密方案在适应性选择密文攻击下的不可区分性(IND-CCA2)
适应性选择密文攻击 （Adaptive Chosen Ciphertext Attack，CCA2）：攻击者获得目标密文后，可以向网络中注入消息（可以和目标密文相关），然后通过和网络中的用户交互，获得与目标密文相应的明文的部分信息

初始化：挑战者产生系统E，攻击者A获得系统的公开钥
训练阶段1：攻击者向挑战者（或解密谕言机）做解密询问（可多次），即取密文c给挑战者，挑战者解密后，将明文给攻击者
挑战：攻击者输出两个长度相同的消息m0和m1，再从挑战者接收mb的密文cb，其中随机值b ∈{ 0,1}
训练阶段2：攻击者继续向挑战者（或解密谕言机）做解密询问（可多次），即取密文c（ c ≠ cb）给挑战者，挑战者解密后将明文给敌手
猜测：攻击者输出b’，如果b’ = b, 则攻击者攻击成功
​在设计抗击主动敌手的密码协议时（如数字签名、认证、密钥交换、多方计算等）， IND-CCA2安全的密码系统是有力的密码原语

原语是指由若干条指令组成的，用于完成 一定功能的一个过程

签名体制的语义安全性(EUF-CMA)
对于数字签名体制，存在以下几种伪造类型

完全攻破：攻击者能够产生与私钥持有者相同的签名，这相当于恢复出了私钥
选择性伪造：攻击者能够伪造一个他选择的消息签名
存在性伪造：攻击者能够伪造一个消息的签名，这个消息可能仅仅是一个随机比特串
签名体制的语义安全性，由不可伪造（Existential Unforgeability）游戏（简称EUF游戏）来刻画

初始阶段：挑战者产生系统E的密钥对(pk,sk) ，攻击者A获得系统的公开钥
阶段1(签名询问)：A执行以下的多项式有界次适应性询问：A提交mi ，挑战者计算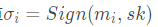

并返回给A
输出：A输出 ( m , σ ) ，如果m不出现在阶段1且 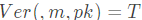，则A攻击成功

签名体制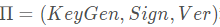

 

 称为在适应性选择消息攻击下具有存在性不可伪造性（Existential Unforgeability Against Adaptive Chosen Messages Attacks，EUF-CMA），简称为EUF-CMA安全，如果对任何多项式有界时间的敌手，存在 一个可忽略的函数negl(k)，使得

 

 

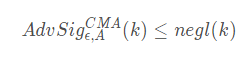
参考文献
[1]刘巍然.如何理解"语义安全(semantic security)"[EB/OL].https://www.zhihu.com/question/37203836/answer/70932036, 2015-11-05.

[2]杨波.密码学中的可证明安全性[M].清华大学出版社,2017年5月.
————————————————
版权声明：本文为CSDN博主「hhh_2333」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_36291381/article/details/106805123