P, NP, NP-complete, NP-hard问题
链接:https://www.zhihu.com/question/24653072/answer/498750995
假设你被关在一个房间里,房间有一扇门,门上有一些开关,假设是 个。你必须将一定数量的开关按下去才能把门打开出去,事先不知道是多少个。现在请问你要花多长时间才能出去?
你别无选择,只能一个个试。答案很明显,正比于房门上的开关数目,对吧?所以这个问题的计算时间可以表示为 ,这里房门上的开关数目n就是问题的规模,次数为1。
现在你出去了,又发现了一扇一模一样的门,那么你还要再花大致一样的时间才能打开。对于两扇门而言你走出去所需要的总时间大约为 ,2就是多项式倍数,次数仍是1,因此解开两扇门时间复杂度还是
。
事实上,无论有多少扇一模一样的门,只要开启的原理不变,你所花费的总时间只会乘以一个系数(就是所谓的多项式倍数),换句话说就是成线性增长的。这就是次数为1(线性)的含义;或者,增加门上的开关数量,哪怕增加一倍甚至几倍,你只要耐心一点,最终还是能出去的。
这回你终于遇到了一扇不一样的门。这个门被分为两部分,每一部分上都有 个开关。你必须在每一部分上都按下特定数量的开关,才能打开门出去。要开启这扇门,你大约需要花费
的时间,可表示为
。虽然看起来很久,但这仍属于多项式时间。
以此类推,如果门分为3部分(每一部分都有 个开关),就需要
的时间;分为
部分,就需要
的时间。无论多少部分都属于多项式时间,表示为
。注意,指数项是个常数,和
无关(和门被分割成的部分数目有关,和每部分上的开关数目无关)。
这里稍微解释一下多项式时间,多项式你总知道吧?形如:
的式子称为关于 的
次多项式。只要问题的计算时间相对于问题大小
可以表示为这样的形式,这个问题就属于多项式时间问题。我们在考虑计算复杂度时,只关注它的最高次项
而将其他低次项以及各项前的系数都忽略掉,记为
。我们将所有此类问题都归为一个大类,P问题。
为什么这个“多项式时间”那么重要而且经常提到?因为它是当今计算科学里,问题“可解”与“不可解”的分水岭。理论上,只要此问题属于P之一大类,目前的计算机都能在可接受的时间内找到问题的最优解;实际上,当指数系数 很大时最优解的寻找也会很困难,但无论如何理论上是可行的。反之,如果计算时间不能表述为这样的形式,我们就将其归为NP问题(非多项式时间)。注意我这里说的“不可解”不是说问题完全无法求解,实际上大部分NP问题,要找到可行解相当容易,但是最优解却几乎无法在可接受的时间内找到。
此外还有一类问题称为NP困难问题,基于现有理论,几乎是肯定不能在多项式时间内进行求解的。下面我们接着开门。
再开了无数扇门以后你遇到了这样一扇门,它上面的开关按下后可以重新拨上去。只有某种特定的开关组合才能把门打开。现在让我们来算一下你需要多长时间开门:每一个开关有拨上去或者按下去两种状态,那么总共有 种状态。假设你把所有开关拨动到每一种状态的时间都差不多,那么总时间就可以表述为
,也就是指数时间。指数时间是一个可怕的敌人。为什么?假设你按下调试所有开关到某个状态需要10秒,如果一共有5个开关,那么你需要320秒试完所有的可能。如果把开关数增加到6个,那么需要的时间将翻一倍到640秒,13个就是81920秒,将近一天的时间。还不够可怕吗?继续增加,增加到22个,你就需要一年多的时间;增加到28个,你一辈子都会困在这个房间里。感受到被指数支配的恐惧了吗?别说是一个人,哪怕天河二号都无法承受这么恐怖的运算时间增幅。
不过,你以为这就是最可怕的情形了吗?你太天真了。
假设你运气好不小心试出了开门的开关组合,下面这个终极Boss才会要了你的命:
你需要按照某种特定的顺序把所有的开关都按一遍,然后才能开门。这个问题的时间复杂度是 ,阶乘,一个比指数更可怕的敌人。
其实上面还有更厉害的 。怪物多得是。只是,解决这种复杂问题已经不属于人的领域了。
有的朋友也许会问,量子计算机能搞定NP问题吗?我的答案是,我也不知道。不过就以上的例子而言,量子计算是可以打开指数的大门的,你可以理解为,具有 个量子比特的计算机,就同时有
个小伙伴在同时帮你尝试各种组合;至于阶乘,大概不行,阶乘除以指数还是阶乘。
P问题:英文为polynomial problem,译过来就是多项式问题。可以在多项式时间内被解决的问题。如果一个问题是P问题,那么毫无疑问我们可以在多项式时间内验证它。
NP问题:英文为Non-deterministic Polynomial problem,不确定性问题。可以在多项式时间内被验证的问题。NP问题可以在多项式时间内被验证,但是不确定是否可以在多项式时间内找出解。通俗来说其解的正确性能够被很容易检查的问题。很容易检查指的是存在一个多项式检查算法。
NP-Hard问题:不确定是否可以在多项式时间内被验证。如果可以证明某问题有一个子问题是NP-Hard问题,那么该问题是一个NP-Hard问题。NP-Hard问题不确定是否可以在多项式时间内被验证。若问题A不属于NP类,已知某一NPC问题可在多项式时间之内转化为问题A,则称A为NP-Hard问题。
NP-Complete问题:是NP的一个子集,且其中每一个问题均能由NP中的任何问题在多项式时间内转化而成。问题A能在多项式时间内转化为问题B,可理解为问题A有一个算法以问题B的算法为子程序,当把每次对B算法的调用看作一个基本操作(只花常数时间)时,A这个算法时多项式时间的。NPC问题是所有NP问题中最难的问题。
证明A是NP-Complete需要两步。第一先证明A是NP的,即满足容易被检查这个性质;第二步是构造一个从某个已知的NP-Complete问题B到A的多项式变换,使得如果B能够被容易求解,A也能被容易解决。我们至少需要知道一个NP-Complete问题。
第一个NP-Complete问题是SAT问题(晚宴安排问题)。COOK证明了任意一个非确定性图灵机的计算过程,即先猜想再验证的过程,都可以被描述成一个SAT问题。如果你有一个能解决该SAT问题的好算法,你就可以解决相应的那个非确定性图灵机计算问题,因为每个NP问题都不过是一个非确定性图灵机计算问题。所以,如果你可以解决SAT,你就可以解决所以NP问题,因此,SAT是一个NP-Complete问题。迄今为止,人们已经发现了成千上万的NP-Complete问题,他们都具有容易被检查的性质。

P, NP, NP-Hard, NP-Complete是不同的复杂性类,用于将所有的算法问题进行分类,以确定当前算法的难度。
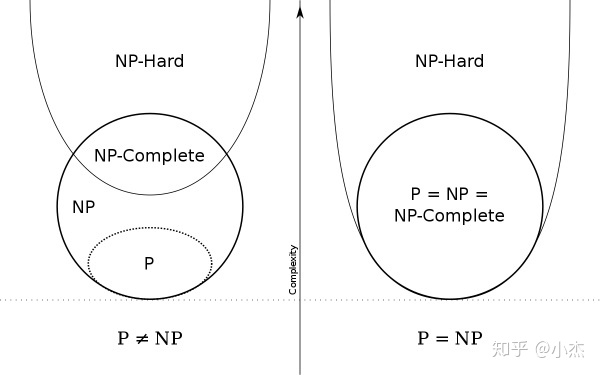
如上图,在所有NP(non-deterministic polynomial-time)问题中(结果正确性可以在多项式时间验证),有些问题是特别难的,如NP-complete问题,有些问题很简单,如P问题,可以在多项式时间解决
那如果我们找到一个特别的问题H,使得所有NP问题都可以reduce到问题H上,那这个问题H肯定特别难,因为我们能用这个问题H解决所有的NP问题,因此我们称这个问题H为NP-Hard问题。
这个经过reduce的问题H不一定是NP问题,于是才有上述示意图的上部分,即有一部分NP hard问题是落在圈外的。如果问题H是属于NP的话,那么问题H就是NP-complete问题,NP完全是NP和NP-hard的交集。
多项式时间可解的问题:如果对于某个确定的常数k,存在一个能在O(nk)时间内求解出某具体问题的算法,就说该具体问题是一个多项式时间可解问题。


