sklearn中 F1-micro 与 F1-macro区别和计算原理
二分类使用Accuracy和F1-score,多分类使用Accuracy和宏F1。
最近在使用sklearn做分类时候,用到metrics中的评价函数,其中有一个非常重要的评价函数是F1值,
在sklearn中的计算F1的函数为 f1_score ,其中有一个参数average用来控制F1的计算方式,今天我们就说说当参数取micro和macro时候的区别
1、准确率,查准率,查全率,F1值:
对于二分类问题,可将样例根据其真实类别和分类器预测类别划分为:
真正例(True Positive,TP):真实类别为正例,预测类别为正例。
假正例(False Positive,FP):真实类别为负例,预测类别为正例。
假负例(False Negative,FN):真实类别为正例,预测类别为负例。
真负例(True Negative,TN):真实类别为负例,预测类别为负例。
然后可以构建混淆矩阵(Confusion Matrix)如下表所示。

#二分类
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
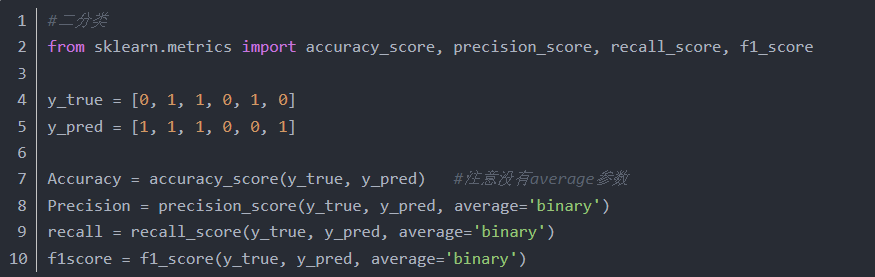
如果只有一个二分类混淆矩阵,那么用以上的指标就可以进行评价,没有什么争议,但是当我们在n个二分类混淆矩阵上要综合考察评价指标的时候就会用到宏平均和微平均。
2、F1_score中关于参数average的用法描述和理解:
通过参数用法描述,想必大家从字面层次也能理解他是什么意思,micro就是先计算所有的TP,FN , FP的个数后,然后再利上文提到公式计算出F1
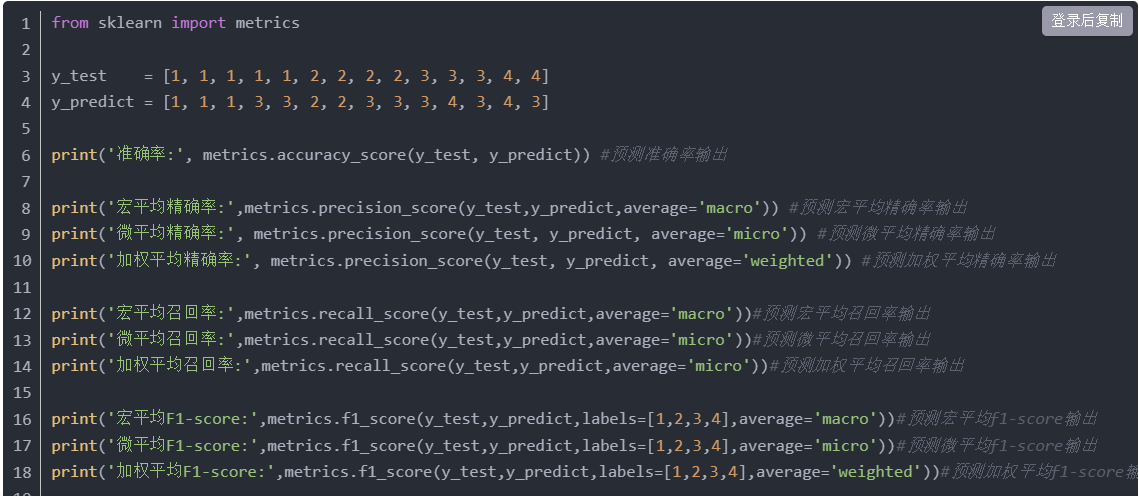
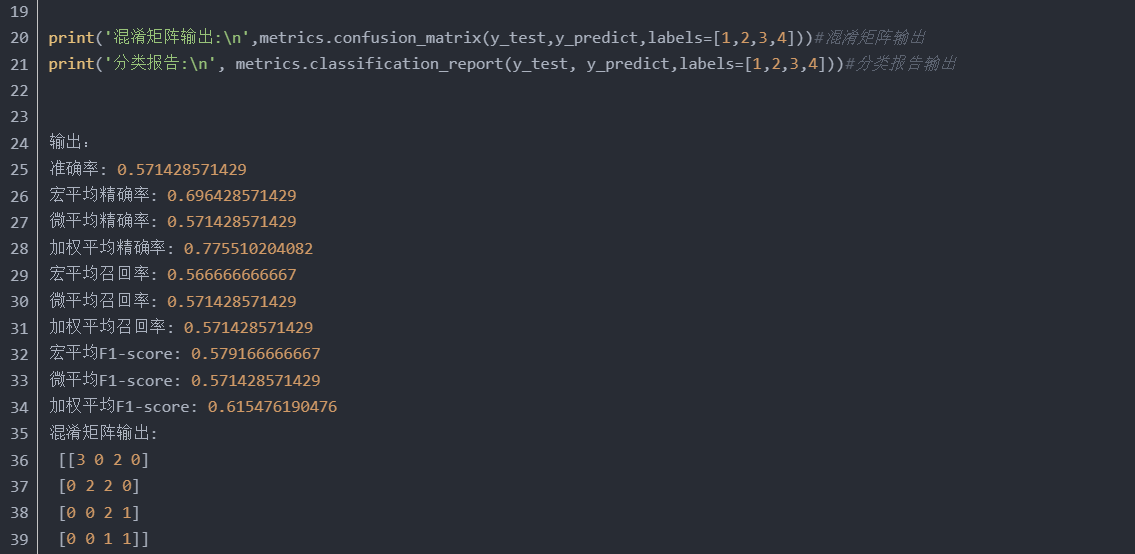
macro其实就是先计算出每个类别的F1值,然后去平均,比如下面多分类问题,总共有1,2,3,4这4个类别,我们可以先算出1的F1,2的F1,3的F1,4的F1,然后再取平均(F1+F2+F3+F4)/4

3、微平均(Micro-averaging)
首先计算总TP值,这个很好就算,就是数一数上面有多少个类别被正确分类,比如1这个类别有3个分正确,2有2个,3有2个,4有1个,那TP=3+2+2+1=8
其次计算总FP值,简单的说就是不属于某一个类别的元数被分到这个类别的数量,比如上面不属于4类的元素被分到4的有1个

如果还比较迷糊,我们在计算时候可以把4保留,其他全改成0,就可以更加清楚地看出4类别下面的FP数量了,其实这个原理就是 One-vs-All (OvA),把4看成正类,其他看出负类

同理我们可以再计算FN的数量

所以micro的 精确度P 为 TP/(TP+FP)=8/(8+4)=0.666 召回率R TP/(TP+FN)=8/(8+6)=0.571 所以F1-micro的值为:0.6153

4、宏平均(Macro-averaging)
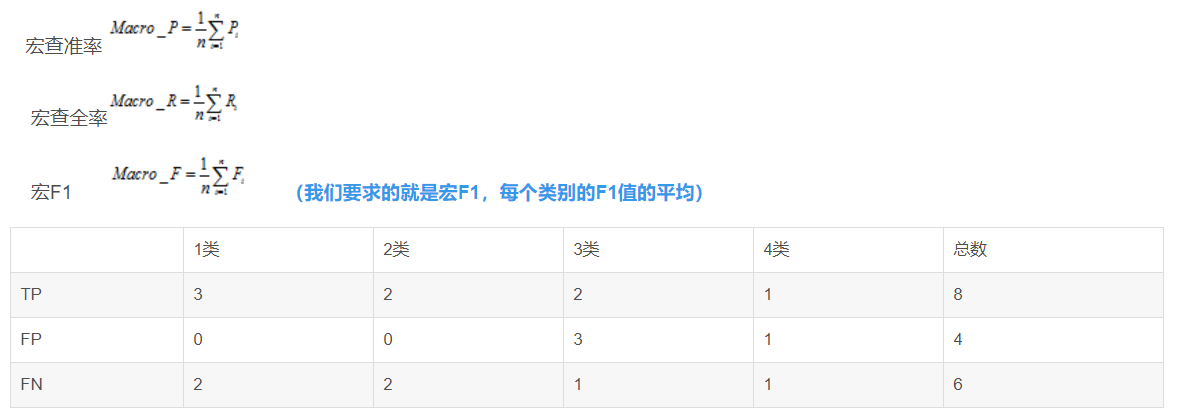
macro先要计算每一个类的F1,有了上面那个表,计算各个类的F1就很容易了,比如1类,它的精确率P=3/(3+0)=1 召回率R=3/(3+2)=0.6 F1=2*(1*0.5)/1.5=0.75
可以sklearn,来计算核对,把average设置成macro
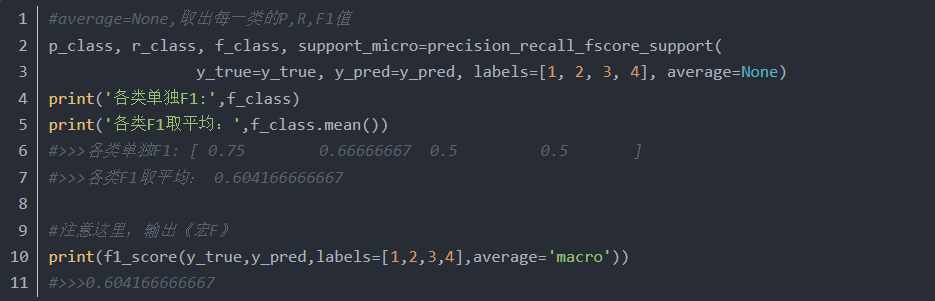
5、sklearn实现
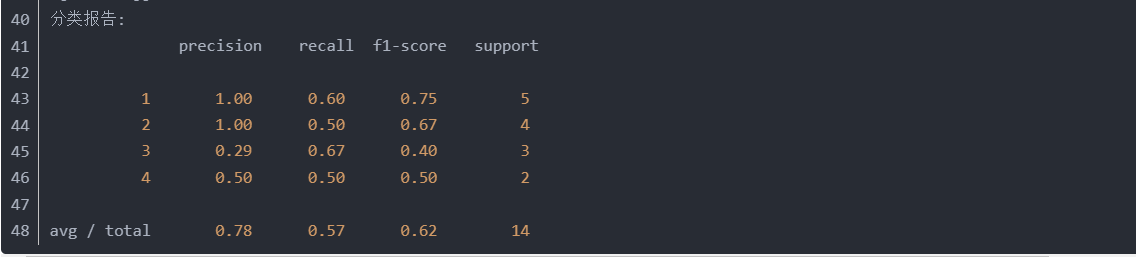
注意:分类报告最后一行为加权平均值。0.64就是加权平均F1-score
https://blog.csdn.net/baidu_38945893/article/details/82141975
f1_score (y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)

①None:返回每一类各自的f1_score,得到一个array。
②'binary': 只对二分类问题有效,返回由pos_label指定的类的f1_score。
Only report results for the class specified by pos_label. This is applicable only if targets (y_{true,pred}) are binary.
③'micro': 设置average='micro'时,Precision = Recall = F1_score = Accuracy。
注意:这是正确的, 微查准率、微查全率、微F1都等于Accuracy。
下例中为什么不等于?因为预测中有几个0,出现错误了。
Note that for “micro”-averaging in a multiclass setting with all labels included will produce equal precision, recall and F_beta.
Calculate metrics globally by counting the total true positives, false negatives and false positives.
④'macro': 对每一类别的f1_score进行简单算术平均(unweighted mean), with assumption that all classes are equally important。
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
⑤'weighted': 对每一类别的f1_score进行加权平均,权重为各类别数在y_true中所占比例。
Calculate metrics for each label, and find their average, weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance; it can result in an F-score that is not between precision and recall.
⑥'samples':
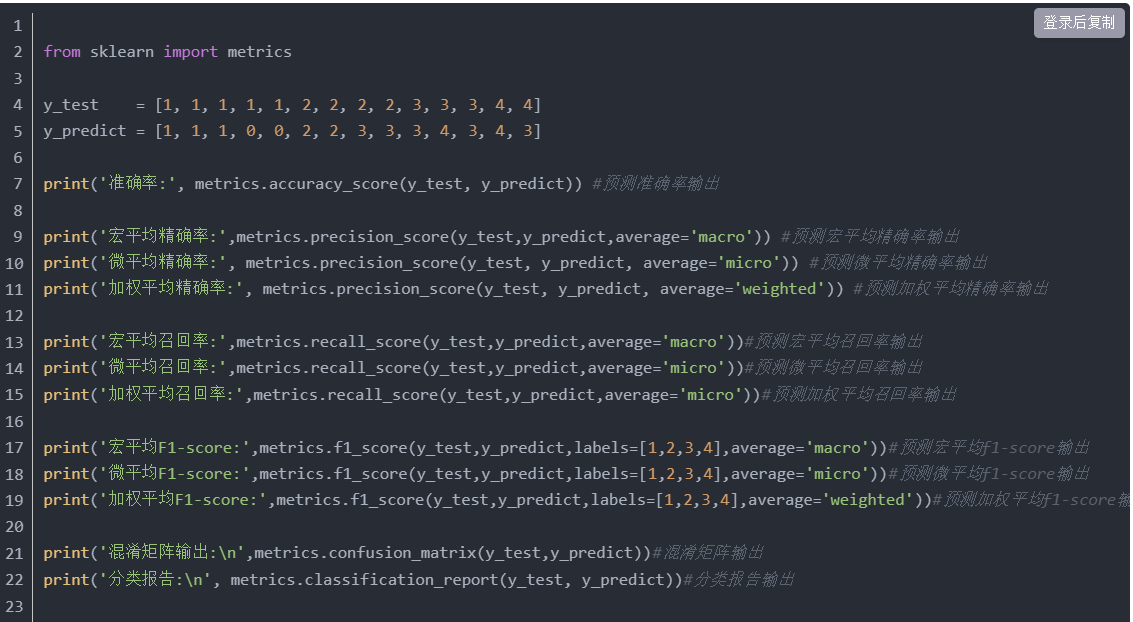

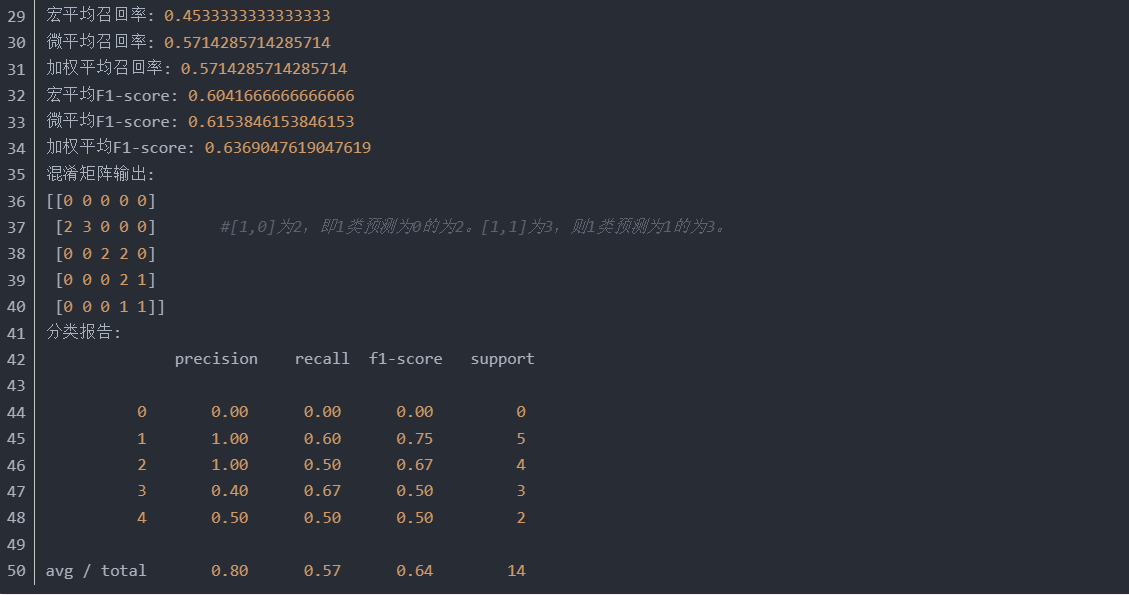
上例有点问题,因为怎么可能预测为0呢?
转载 https://blog.csdn.net/lyb3b3b/article/details/84819931
还可参考
https://www.cnblogs.com/techengin/p/8962024.html
https://zhuanlan.zhihu.com/p/64315175
https://blog.csdn.net/qq_43190189/article/details/105778058
https://blog.csdn.net/sinat_28576553/article/details/80258619
————————————————
版权声明:本文为CSDN博主「飞翔的大马哈鱼」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/lyb3b3b/article/details/84819931


 浙公网安备 33010602011771号
浙公网安备 33010602011771号