马氏距离
马氏距离就是将数据做了旋转,做了方差归一化之后再计算的欧氏距离
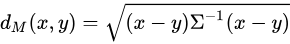
马氏距离在欧式距离的基础上增加了(公司中x、u表示两个不同的变量):
1. (xi-uj),欧式距离只有(xi-uj),即相同下标的x-u的乘积
2. (xi-ui)(xj-uj)的前面增加了一个系数,这个系数是xi和ui的协方差(协方差表示两个变量的相关性,正相关或负相关)
所以,使用了马氏距离,在不同的坐标维度上,比如i和j,距离单位不是等长的。比如在i坐标上,xi=2,yi=1,在j坐标上,xj=2,yj=1,这两个点在其对应的坐标上的马氏距离是和(xi,yi),(xj,yj)各自的相关性有关的。他们的马氏距离并不相等。ai(xi-yi)和aj(xj-yj),当他们没有相关性的时候,即ai=aj=1,这时,马氏距离变为欧式距离。
另外,马氏距离等价于在具有相关性的坐标系内进行一个变换,变换到一个无相关性的坐标系内求欧氏距离
https://www.zhihu.com/question/35211238
Preface
之前在写《Multi-view CNNs for 3D Objects Recognition》的阅读笔记的时候,文章中的一个创新点便是将MVCNN网络提取到的3D Objects的形状特征描述符,投影到马氏距离(Mahalanobis Distance)上,“这样的话,相同类别3D形状之间的ℓ2距离在投影后的空间中就更小,而不同的类别之间的ℓ2在投影后会更大”,也更适用于3D形状的分类与检索。
后来我沿着这篇文章继续追踪这个马氏距离,发现在2013年BMVC会议上的《Fisher Vector Faces in the Wild》,2008年的PR会议上的《Learning a Mahalanobis distance metric for data clustering and classification》,这两篇文章都使用了马氏距离进行衡量特征向量之间的“远近”。
因此,我想搞清楚马氏距离以及欧式距离之间的区别。本文是之为记。
Basis
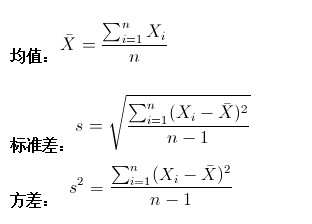
方差:方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集。
标准差计算公式:
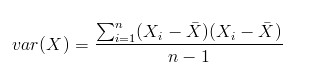
协方差:标准差与方差是描述一维数据的,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
协方差矩阵,当变量多了,超过两个变量了。那么,就用协方差矩阵来衡量这么多变量之间的相关性。假设 是以 个随机变数(其中的每个随机变数是也是一个向量,当然是一个行向量)组成的列向量:
其中, 是第 个元素的期望值,即 。协方差矩阵的第 项(第 项是一个协方差)被定义为如下形式:
即: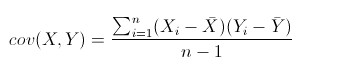
假设数据集有三个维度,则协方差矩阵为
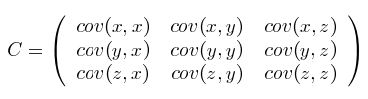
如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义)。
当 cov(X, Y)>0时,表明X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
这就是协方差的意义
协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
Mahalanobis Distance & Euclidean Distance
Definition
马氏距离(Mahalanobis Distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。
对于一个均值为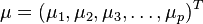
,协方差矩阵为Σ的多变量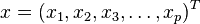
,其马氏距离为: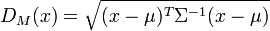
如果 是单位阵的时候,马氏距离简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的马氏距离。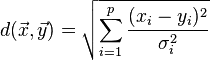
其中σi是xi的标准差。
Why is Mahalanobis distance?
马氏距离有很多优点,马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。
它的缺点是夸大了变化微小的变量的作用。
这个stackexchange问答很好的回答了马氏距离的解释:
下图是一个二元变量数据的散点图:
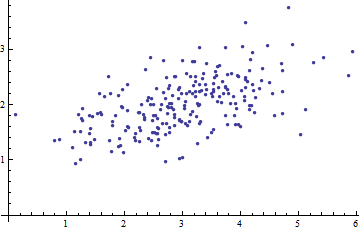
当我们将坐标轴拿掉,如下图,我们能做些什么呢?
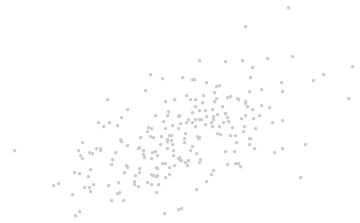
那就是根据数据本身的提示信息来引入新的坐标轴 。
坐标的原点在这些点的中央(根据点的平均值算得)。第一个坐标轴(下图中蓝色的线)沿着数据点的“脊椎”,并向两端延伸,定义为使得数据方差最大的方向。第二个坐标轴(下图红色的线)会与第一个坐标轴垂直并向两端延伸。如果数据的维度超过了两维,那就选择使得数据方差是第二个最大的方向,以此类推。
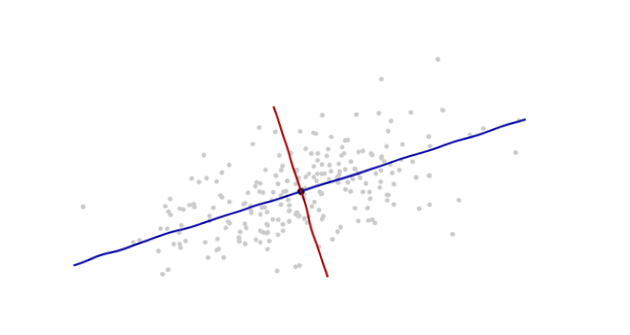
我们需要一个 比例尺度 。用数据沿着每一个坐标轴的标准差来定义一个单位长度。要记住 68-95-99.7 法则:大约2/3的点需要在离原点一个单位长度的范围内;大约95%的点需要在离原点两个单位的长度范围内;这会使得我们更紧盯着正确的单元。为了以示参考,如下图:
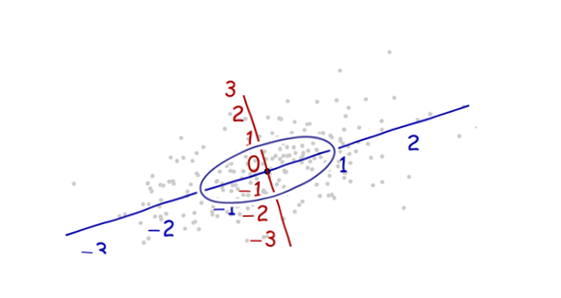
上图并不像是一个圆,对吧?那是因为这幅图是被扭曲的(图中,不同轴上的单位长度不一样)。因此,让我们重新沿着正确的方向画图——从左到右,从下到上( 相当于旋转一下数据 )。同时, 并让每个轴方向上的单位长度相同 ,这样横坐标上一个单位的长度就与纵坐标上的单位长度相同。
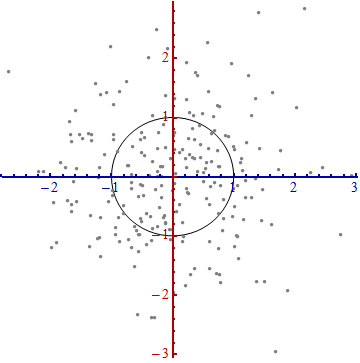
这里发生了什么?我们让数据告诉我们怎样去从散点图中构建坐标系统,以便进行测量。这就是上面所要表达的内容。尽管在这样的过程中我们有几种选择(我们可以将两个坐标轴颠倒;在少数的几种情况下,数据的“脊椎”方向——主方向,并不是唯一的),但是这些在最后并不影响距离。
Technical comments
沿着新坐标轴的单位向量是协方差矩阵的特征向量。
注意到没有变形的椭圆,变成圆形后沿着特征向量用标准差(协方差的平方根)将距离长度分割。用代表协方差函数,点之间的距离(Mahalanobis distance)就是之间以方差的平方根为单位长度所分割产生的长度:。对应的代数式是,。这个公式不管用什么基底表示向量以及矩阵时都成立。特别是,这个公式在原始的坐标系中对于Mahalanobis Distance的计算也正确。
在最后一步中,坐标轴扩展的量是协方差矩阵的逆的特征值(平方根),同理的,坐标轴缩小的量是协方差矩阵的特征值。所以,点越分散,需要的将椭圆转成圆的缩小量就越多。
尽管上述的操作可以用到任何数据上,但是对于多元正态分布的数据表现更好。在其他情况下,点的平均值或许不能很好的表示数据的中心,或者数据的“脊椎”(数据的大致趋势方向)不能用变量作为概率分布测度(using variance as a measure of spread)来准确的确定。
原始坐标系的平移、旋转,以及坐标轴的伸缩一起形成了仿射变换(affine transformation)。除了最开始的平移之外,其余的变换都是基底变换,从原始的一个变为新的一个。
对于多元正太分布,Mahalanobis 距离(已经变换到新的原点)出现在表达式中的位置,描述标准正太分布的概率密度。因此,在新的坐标系中,多元正态分布像是标准正太分布,当将变量投影到任何一条穿过原点的坐标轴上。特别是,在每一个新的坐标轴上,它就是标准正态分布。从这点出发来看,多元正态分布彼此之实质性的差异就在于它们的维度。注意,这里的维数可能,有时候会少于名义上的维数。
假设数据分布是一个二维的正椭圆,轴轴均值都为0,轴的方差为1000,轴的方差为1,考虑两个点到原点的距离,如果计算的是欧氏距离那么两者相等,但是仔细想一下,因为x轴的方差大,所以应该是更接近中心的点,也就是正态分布标准差的原则。这时候需要对轴进行缩放,对应的操作就是在协方差矩阵的对角上加上归一化的操作,使得方差变为1.
假设数据分布是一个二维的椭圆,但是不是正的,比如椭圆最长的那条线是的,因为矩阵的对角只是对坐标轴的归一化,如果不把椭圆旋转回来,这种归一化是没有意义的,所以矩阵上的其他元素(非对角)派上用场了。如果椭圆不是正的,说明变量之间是有相关性的(x大y也大,或者负相关),加上协方差非对角元素的意义就是做旋转。
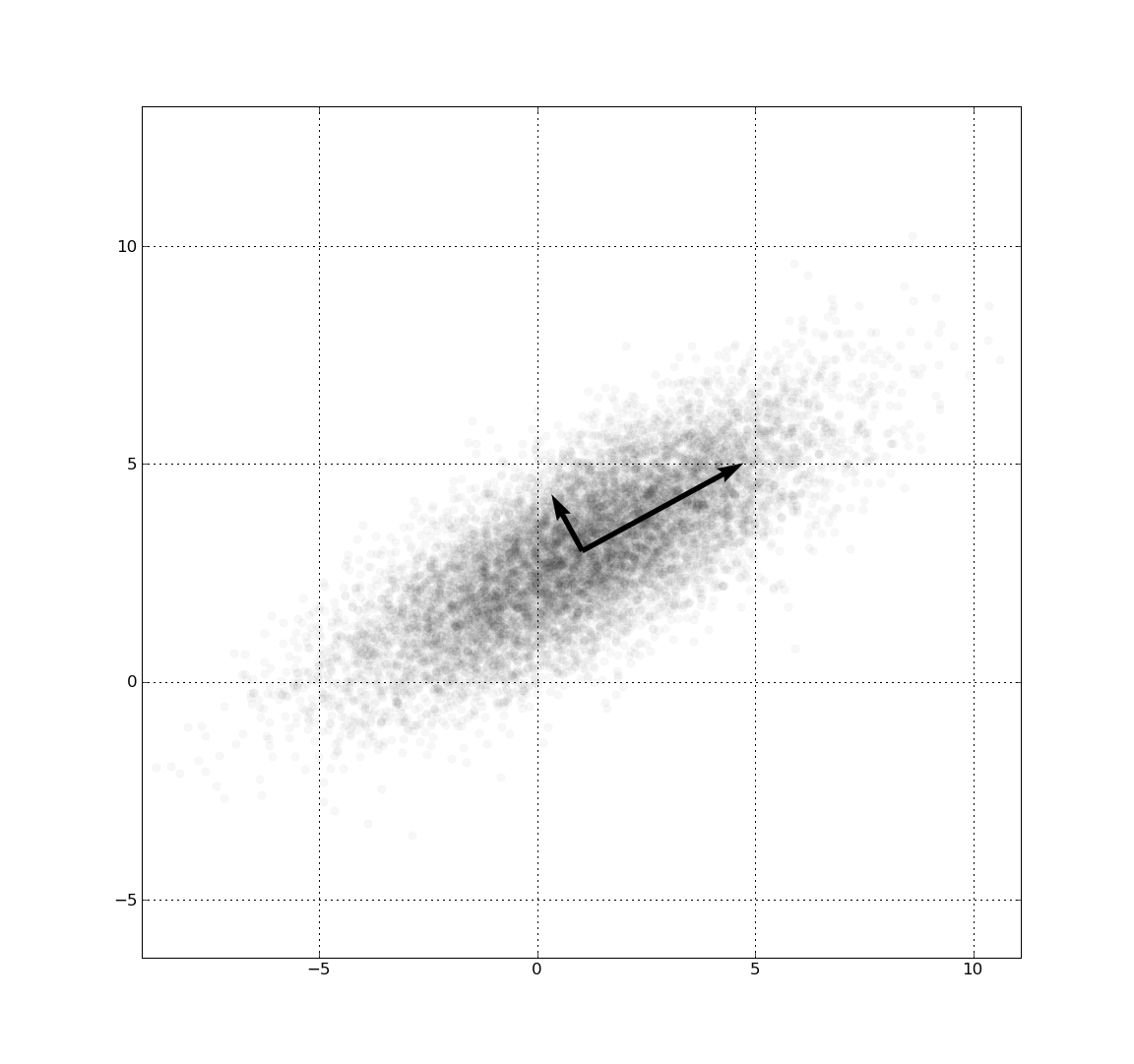
上图是,一个左下右上方向标准差为 3,正交方向标准差为 1 的多元高斯分布的样本点。由于 x 和 y 分量共变(即相关),x 与 y 的方差不能完全描述该分布;箭头的方向对应的协方差矩阵的特征向量,其长度为特征值的平方根。
http://blog.csdn.net/u010167269/article/details/51627338?_t_t_t=0.0028043033089488745
Reference
https://en.wikipedia.org/wiki/Mahalanobis_distance
https://zh.wikipedia.org/wiki/%E9%A9%AC%E6%B0%8F%E8%B7%9D%E7%A6%BB
http://blog.csdn.net/lanbing510/article/details/8758651
http://www.zhizhihu.com/html/y2009/261.html
http://stats.stackexchange.com/questions/62092/bottom-to-top-explanation-of-the-mahalanobis-distance
https://www.zybuluo.com/Antosny/note/108773
https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5
————————————————
版权声明:本文为CSDN博主「Catherine_985」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Catherine_985/article/details/78933387



