Python机器学习笔记:异常点检测算法——Isolation Forest
完整代码及其数据,请移步小编的GitHub
传送门:请点击我
如果点击有误:https://github.com/LeBron-Jian/MachineLearningNote
孤立森林(isolation Forest)是一种高效的异常检测算法,它和随机森林类似,但每次选择划分属性和划分点(值)时都是随机的,而不是根据信息增益或基尼指数来选择。下面学习一个孤立森林的理论和使用。
单样本检测算法One Class SVM 可以参考下面博客:
Python机器学习笔记:异常点检测算法——One Class SVM
前言
1,异常点检测算法使用场景
什么时候我们需要异常点检测算法呢?常用的有三种情况。
- 1.做数据预处理的时候需要对异常的数据做过滤,防止对归一化等处理的结果。
- 2.对没有标记输出的特征数据做筛选,找出异常的数据。
- 3.对有标记输出的特征数据做二分类时,由于某些类别的训练样本非常少,类别严重不平衡,此时也可以考虑用非监督的异常点检测算法来做。
在以上场景中,异常的数据量都是很少的一部分,因此诸如:SVM,逻辑回归等分类算法,都不适用,因为监督学习算法适用于有大量的正向样本,也有大量的负向样本,有足够的样本让算法去学习其特征,且未来新出现的样本与训练样本分布一致。
下面是异常检测和监督学习相关算法的适用范围:
- 异常检测:信用卡诈骗,制造业产品异常检测,数据中心机器异常检测,入侵检测
- 监督学习:垃圾邮件识别,新闻分类,
2,异常点检测算法常见类别
异常点检测的目的是找到数据集中和大多数数据不同的数据,常用的异常点检测算法一般分为三类。
第一类是基于统计学的方法来处理异常数据,这种方法一般会构建一个概率分布模型,并计算对象符合该模型的概率,把具有低概率的对象视为异常点。比如特征工程中的RobustScaler方法,在做数据特征值缩放的时候,它会利用数据特征的分位数分布,将数据根据分位数划分为多段,只取中间段来做缩放,比如只取25%分位数到75%分位数的数据做缩放,这样减少了异常数据的影响。
第二类是基于聚类的方法来做异常点检测。这个很好理解,由于大部分聚类算法是基于数据特征的分布来做的,通常我们聚类后发现某些聚类簇的数据样本量比其他簇少很多,而且这个簇里的数据特征均值分布之类的值和其他簇也差异很大,这些簇里的样本点大部分时候都是异常点。比如BIRCH聚类算法原理和DBSCAN密度聚类算法都可以在聚类的同时做异常点的检测。
第三类是基于专门的异常点检测算法来做。这些算法不像聚类算法,检测异常点只是一个赠品,他们的目的就是专门检测异常点的,这类算法的代表是One Class SVM 和Isolation Forest。
1,Isolation Forest 算法
1.1 Isolation Forest算法概述
Isolation,意为孤立/隔离,是名词,其动词为isolate,forest是森林,合起来就是“孤立森林”了,也有叫“独异森林”,好像并没有统一的中文叫法。可能大家都习惯用其英文的名字isolation forest,简称iForest 。
iForest算法是由南京大学的周志华和澳大利亚莫纳什大学的Fei Tony Liu,Kai Ming Ting等人共同移除,用于挖掘数据,它是适用于连续数据(Continuous numerical data)的异常检测,将异常定义为“容易被孤立的离群点(more likely to be separated)”——可以理解为分布稀疏且离密度高的群体较远的点。用统计学来解释,在数据空间里面,分布稀疏的区域表示数据发生在此区域的概率很低,因此可以认为落在这些区域里的数据是异常的。通常用于网络安全中的攻击检测和流量异常等分析,金融机构则用于挖掘出欺诈行为。对于找出的异常数据,然后要么直接清除异常数据,如数据清理中的去噪数据,要么深入分析异常数据,比如分析攻击,欺诈的行为特征。
1.2 Isolation Forest算法原理
iForest 属于Non-parametric和unsupervised的方法,即不用定义数学模型也不需要有标记的训练。对于如何查找哪些点是否容易被孤立(isolated),iForest使用了一套非常高效的策略。假设我们用一个随机超平面来切割(split)数据空间(data space),切一次可以生成两个子空间(详细拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每个子空间里面只有一个数据点为止。直观上来讲,我们可以发现那些密度很高的簇是被切分很多次才会停止切割,但是那些密度很低的点很容易很早就停到一个子空间看了。
iForest 算法得益于随机森林的思想,与随机森林由大量决策树组成一样,iForest森林也由大量的二叉树组成,iForest 中的树叫 isolation tree,简称 iTree,iTree 树和决策树不太一样,其构建过程也比决策树简单,是一个完全随机的过程。
假设数据集有 N 条数据,构建一颗 ITree时,从 N条数据中均匀抽样(一般是无放回抽样)出 n 个样本出来,作为这棵树的训练样本。在样本中,随机选出一个特征,并在这个特征的所有值范围内(最小值和最大值之间)随机选一个值,对样本进行二叉划分,将样本中小于该值的划分到节点的左边,大于等于该值的划分到节点的右边。由此得到一个分裂条件和左右两边的数据集,然后分别在左右两边的数据集上重复上面的过程,直到数据集只有一条记录或者达到了树的限定高度。
由于异常数据较小且特征值和正常数据差别很大。因此,构建 iTree的时候,异常数据离根更近,而正常数据离根更远。一颗ITree的结果往往不可信,iForest算法通过多次抽样,构建多颗二叉树。最后整合所有树的结果,并取平均深度作为最终的输出深度,由此计算数据点的异常分支。
下图为iForest 构建 iTree 示例,异常数据点(17, 17)通常离根节点很近。

2,Isolation Forest算法步骤
怎么来切这个数据空间是iForest的设计核心思想,本文仅学习最基本的方法,由于切割是随机的,所以需要用ensemble的方法来得到一个收敛值(蒙特卡洛方法),即反复从头开始切,然后平均每次切的结果。IForest由 t个iTree(Isolation Tree)孤立树组成,每个iTree是一个二叉树结构,所以下面我们先说一下iTree树的构建,然后再看iForest树的构建。
2.1 iTree 的构建
提到森林,自然少不了树,毕竟森林都是树构建的,看Isolation Forest(简称iForest)前,我们先来看看Isolation Tree(简称iTree)是怎么构成的。iTree是一种随机二叉树,每个节点要么有两个女儿,要么就是叶子节点,一个孩子都没有。给定一堆数据集D,这里D的所有属性都是连续型的变量,iTree的构成过程如下:
1,随机选择一个属性Attr
2,随机选择该属性的一个值Value
3,根据Attr 对每条记录进行分类,把Attr小于Value的记录放在左女儿,把大于等于Value的记录放在右孩子。
4,然后递归的构造左女儿和右女儿,直到满足以下条件:
- 1,传入的数据集只有一条记录或者多条一样的记录
- 2,树的高度达到了限定高度

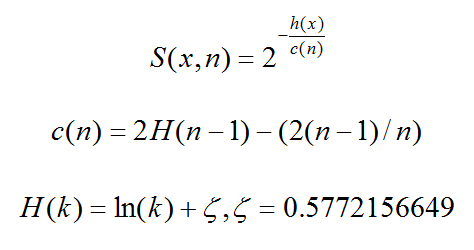
S(x,n) 就是记录x在n个样本的训练数据构成的iTree的异常指数,S(x,n)取值范围为[0,1]。
就是记录 x 在由 n 个样本的训练数据构成 iTree 的异常指数,取值范围为[0, 1],异常情况的判断分以下几种情况
- 1,越接近1表示是异常点的可能性高
- 2,越接近0表示是正常点的可能性高
- 3,如果大部分的训练样本的S(x,n)都接近于0.5,说明整个数据集都没有明显的异常值
2.2 iForest的构建
iTree明白了,下面我们看看IForest是怎么构造的,给定一个包含n条记录的数据集D,如何构造一个iForest,iForest和Random Forest的方法有点类似,都是随机采样一部分数据集去构造一棵树,保证不同树之间的差异性,不过iForest与RF不同,采样的数据量Psi不需要等于n,可以远远小于n,论文提到采样大小超过256效果就提升不大了,并且越大还会造成计算时间上的浪费,为什么不像其他算法一样,数据越多效果越好呢?可以看看下面这两个图:
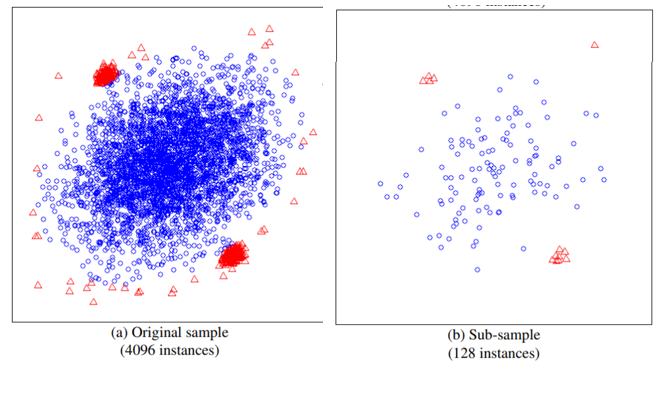
左边是原始数据,右边是采样了数据,蓝色是正常样本,红色是异常样本。可以看到,在采样之前,正常样本和异常样本出现重叠,因此很难分开,但我们采样之和,异常样本和正常样本可以明显的分开。
其构造 iForest 的步骤如下:
- 1,从训练数据中随机选择 n 个点样本作为subsample,放入树的根节点。
- 2,随机指定一个维度(attribute),在当前节点数据中随机产生一个切割点p——切割点产生于当前节点数据中指定维度的最大值和最小值之间。
- 3,以此切割点生成了一个超平面,然后将当前节点数据空间划分为2个子空间:把指定维度里面小于p的数据放在当前节点的左孩子,把大于等于p的数据放在当前节点的右孩子。
- 4,在孩子节点中递归步骤2和3,不断构造新的孩子节点,知道孩子节点中只有一个数据(无法再继续切割)或者孩子节点已达限定高度。
除了限制采样大小之外,还要给每棵 iTree 设置最大高度,这是因为异常数据记录都比较少,其路径长度也比较低,而我们也只需要把正常记录和异常记录区分开来,因此只需要关心低于平均高度的部分就好,这样算法效率更高,不过这样调整了后,后面可以看到计算需要一点点改进,先看iForest的伪代码:

获得 t个iTree之后,iForest训练就结束,然后我们可以用生成的iForest来评估测试数据了。对于一个训练数据X,我们令其遍历每一颗iTree,然后计算X 最终落在每个树第几层(X在树的高度)。然后我们可以得到X在每棵树的高度平均值,即 the average path length over t iTrees。
2.3 iForest 预测
IForest构造好之后,对测试进行预测,需要进行综合每棵树的结果,于是 PathLength 表示记录 x 在每棵树的高度均值,另外计算需要改进,在生成叶子节点时,算法记录了叶子节点包含的记录数量,这时候需要用这个数量估计一下平均高度的,其计算方法如下:

在处理高维数据时,可以对算法进行改进,采样之后并不是把所有的属性都用上,而是用峰度系数Kurtosis挑选一些有价值的属性,再进行iTree的构造,这跟随机森林就更像了,随机选记录,再随机选属性。
3,Isolation Forest算法总结
3.1 小结1
IForest目前是异常点检测最常用的算法之一,它的优点非常突出,他具有线性时间复杂度。因为是随机森林的方法,所以可以用在含有海量数据的数据集上,通常树的数量越多,算法越稳定。由于每棵树都是互相独立生成的,因此可以部署在大规模分布式系统上来加速运算。对于目前大数据分析的趋势来说,它的好用是由原因的。
但是IForest也有一些缺点,比如不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度和该维度的随机一个特征,建完树后仍然有大量的维度没有被使用,导致算法可靠性降低。此推荐降维后使用,或者考虑使用One Class SVM 。
另外IForest仅对即全局稀疏点敏感,不擅长处理局部的相对稀疏点,这样在某些局部的异常点较多的时候检测可能不是很准。
而One Class SVM对于中小型数据分析,尤其是训练样本不是特别海量的时候用起来经常会比IForest顺手,因此比较适合做原型分析。
3.2 小结2
- 1,iForest具有线性时间复杂度,因为是ensemble的方法,所以可以用在含有海量数据的数据集上面,通常树的数量越多,算法越稳定。由于每棵树都是相互独立生成的,因此可以部署在大规模分布式系统上来加速运算。
- 2,iForest不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度,建完树后仍然有大量的维度信息没有被使用,导致算法可靠性降低。高维空间还可能存在大量噪音维度或者无关维度(irrelevant attributes),影响树的构建。对这类数据,建议使用子空间异常检测(Subspace Anomaly Detection)技术。此外,切割平面默认是axis-parallel的,也可以随机生成各种角度的切割平面。
- 3,IForest仅对Global Anomaly敏感,即全局稀疏点敏感,不擅长处理局部的相对稀疏点(Local Anomaly)。
- 4,iForest推动了重心估计(Mass Estimation)理论,目前在分类聚类和异常检测中都取得显著效果。
Isolation Forest 算法主要有两个参数:一个是二叉树的个数;另一个是训练单棵ITree时候抽取样本的数目。实验表明,当设定为100棵树,抽样样本为256条的时候,iForest 在大多数情况下就可以取得不错的效果。这也体现了算法的简单,高效。
Isolation Forest 是无监督的异常检测算法,在实际应用中,并不需要黑白标签。需要注意的是:(1)如果训练样本中异常样本的比例比较高,违背了先前提到的异常检测的基本假设,可能最终的效果会受到影响;(2)异常检测根具体的应用场景紧密相关,算法检测出的“异常”不一定是我们实际想要的,比如,在识别虚假交易时,异常的交易未必就是虚假的交易。所以,在特征选择时,可能需要过滤不太相关的特征,以免识别出一些不太相关的“异常”。
4,scikit-learn Isolation Forest算法库概述
在sklearn中,我们可以用ensemble包里面的IsolationForest来做异常点检测
4.1 知识储备(np.random.RandomState的用法)
numpy.random.RandomState():获取随机数生成器
是计算机实现的随机数生成通常为伪随机数生成器,为了使得具备随机性的代码最终的结果可复现,需要设置相同的种子值。
|
1
2
3
|
rng = numpy.random.RandomState(123465)arrayA = rng.uniform(0,1,(2,3)) |
该段代码的目的是产生一个2行3列的assarray,其中的每个元素都是[0,1]区间的均匀分布的随机数。
这里可以看到123456这个数字,其实,他是伪随机数产生器的种子。也就是“the starting point for a sequence of pseudorandom number”
对于某一个伪随机数发生器,只要该种子(seed)相同,产生的随机数序列就是相同的。
4.2 iForest常用参数解释
- n_estimators:构建多少个itree,int,optional (default=100)指定该森林中生成的随机树数量
- max_samples:采样数,自动是256,int,optional(default='auto)
用来训练随机数的样本数量,即子采样的大小:
(1)如果设置的是一个int常数,那么就会从总样本 X 拉取 max_samples个样本生成一棵树iTree
(2)如果设置的是一个float浮点数,那么就会从总样本 X 拉取 max_samples*X.shape[0] 个样本,X.shape[0] 表示总样本个数
(3) 如果设置的是 “auto”,则max_samples=min(256, n_samples),n_samples即总样本的数量
如果max_samples 值比提供的总样本的数量还大的话,所有的样本都会用来构造数,意思就是没有采样了,构造的 n_estimators棵ITree使用的样本都是一样的,即所有的样本
- contamination:c(n)默认是0.1,float in (0, 0.5),optional(default=0.1),取值范围为(0, 0.5),表示异常数据占给定的数据集的比例,就是数据集中污染的数量,定义该参数值的作用是在决策函数中定义阈值。如果设置为“auto”,则决策函数的阈值就和论文一样,在版本0.20中有变换:默认值从0.1变为0.22的auto。
- max_features:最大特征数,默认为1,int or float,optional,指定从总样本X中抽取来训练每棵树iTree 的属性的数量,默认只使用一个属性
如果设置为 int 整数,则抽取 max_features 个属性
如果是float浮点数,则抽取 max_features *X.shape[1] 个属性
- bootstrap:boolean,optional(default = False),构建Tree时,下次是否替换采样,为True为替换,则各个树可放回地对训练数据进行采样;为False为不替换,即执行不放回的采样
- n_jobs:int or None, optional (default = None), 在运行 fit() 和 predict() 函数时并行运行的作业数量。除了在 joblib.parallel_backend 上下文的情况下,None表示为1,设置为 -1 则表示使用所有可以使用的处理器
- behaviour:str,default='old',决策函数 decision_function 的行为,可以是“old”和‘new’。设置为 behavior='new'将会让 decision_function 去迎合其它异常检测算法的API,这在未来将会设置为默认值。正如在 offset_ 属性文档中详细解释的那样,decision_function 变得依赖于 contamination 参数,以 0 作为其检测异常值的自然阈值。
New in version 0.20:behaviour参数添加到了0.20版本中以实现后向兼容
behaviour='old'在0.20版本中以经弃用,在0.22版本中将不能使用
behaviour参数将在0.22版本中弃用,将在0.24版本中移除
- random_state:int,RandomState instance or None,optional(default=None)
如果设置为 int 常数,则该 random_state 参数值是用于随机数生成器的种子
如果设置为RandomState实例,则该 random_state 就是一个随机数生成器
如果设置为None,则该随机数生成器就是使用在 np.random中RandomState实例
- verbose:int,optional(default=0)控制树构建过程的冗长性
- warm_start:bool,optional(default=False),当设置为TRUE时,重用上一次调用的结果去 fit,添加更多的树到上一次的森林1集合中;否则就 fit一整个新的森林
完整的参数,请参考scikit-learn官网文档,这里方便自己学习,就复制到这里。


4.3 iForest常用属性说明

- estimators_:构造好的子树的集合
- estimators_samples:每个子树抽取的样本的子集
- max_samples_:样本的真正数量
- offset_:float
- offset用来从原始分数开始定义决策函数,其关系是decision_function = score_samples - offset_。假设behaviour == ‘new’,则offset_如下定义:
当contamination参数设置为'auto',当inliers的得分接近0且outliers的得分接近-1时,偏移量等于-0.5;
当提供与“auto”不同的contamination参数时,则以在训练中获取期望的异常个数的方式来定义偏移量(决策函数< 0的样本)。
假设behaviour ==“old”,我们总是有offset_ = -0.5,使得决策函数独立于contamination参数。
- 注意:其实现是基于一系列的ExtraTreeRegressor。每个树的最大深度设置为ceil(log_2(n)),其中n是用于构建树的样本数量
4.4 iForest常用方法介绍

解释几个常用的:
- score_samples(X):与原文定义的异常值相反
- set_params(**params):设置该森林的参数
4.5 实例一(iForest算法检验数据)
The IsolationForest 'isolates' observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature.
isolation Forest 通过随机选择一个特征然后随机选择所选特征的最大值和最小值之间的分割值来“隔离”观察。
Since recursive partitioning can be represented by a tree structure, the number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.
由于递归分区可以表示为一个树结构,分裂需要隔离一个样本的数量相当于从根节点到终止节点路径长度。
The path length , averaged over a forest of such random trees, is a measure of normality and our decision function.
Random partitioning produces noticeable shorter paths for anomalies. Hence, when a forest of random trees collectively produce shorter path lenghts for particular samples, they are highly likely to be anomalies.
随机划分为异常生产明显更短的路径。因此,当一个随机森林产生短路径长度,他们极有可能是异常点。
代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
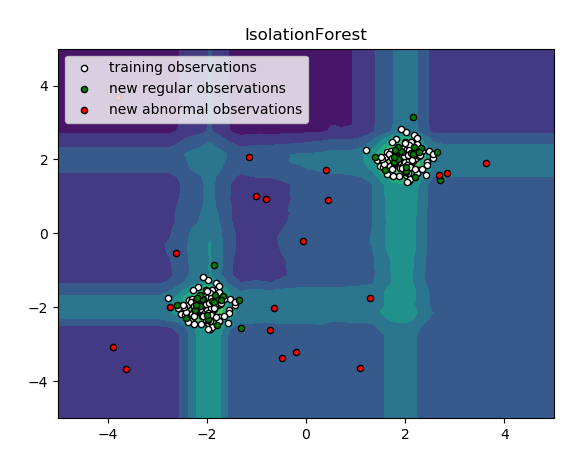
#_*_coding:utf-8_*_import numpyas npimport matplotlib.pyplotas pltfrom sklearn.ensemble import IsolationForestrng = np.random.RandomState(42)# Generate train dataX = 0.3 * rng.randn(100, 2)X_train = np.r_[X + 2, X - 2]X = 0.3 * rng.randn(20, 2)X_test = np.r_[X + 2, X - 2]X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))# fit the modelclf = IsolationForest(behaviour='new', max_samples=100, random_state=rng, contamination='auto')clf.fit(X_train)y_pred_train = clf.predict(X_train)y_pred_test = clf.predict(X_outliers)xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.title("IsolationForest")plt.contourf(xx, yy, Z, camp=plt.cm.Blues_r)b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=20, edgecolor='k')b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green', s=20, edgecolor='k')c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red', s=20, edgecolor='k')plt.axis('tight')plt.xlim((-5, 5))plt.ylim((-5, 5))plt.legend([b1, b2, c], ["training observations", "new regular observations","new abnormal observations"], loc="upper left")plt.show() |
结果展示:
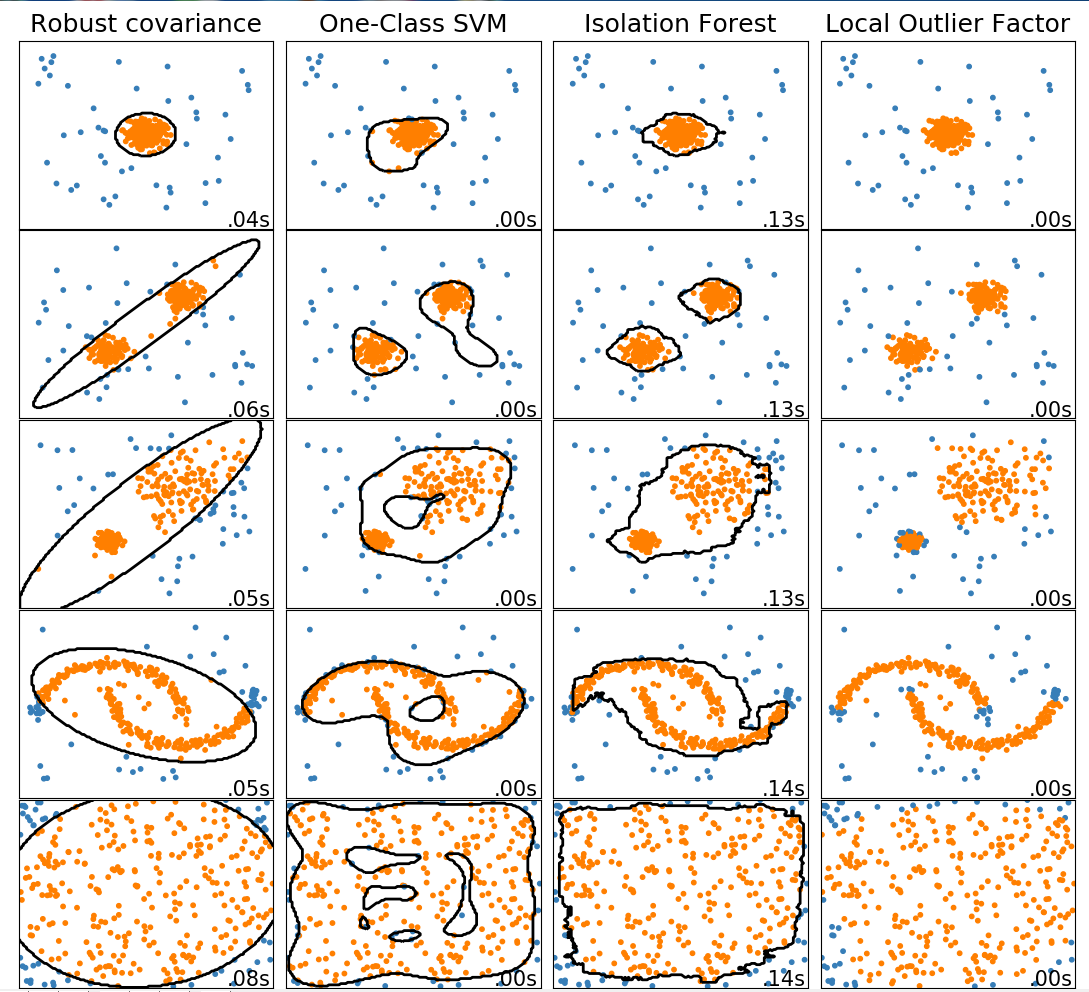
4.6 实例二(多种异常检测算法比较)
此示例显示了2D数据集上不同异常检测算法的特征。数据集包含一种或两种模式(高密度区域),以说明算法处理多模态数据的能力。
对于每个数据集,15%的样本被生成为随机均匀噪声。该比例是给予OneClassSVM的nu参数的值和其他异常值检测算法的污染参数。除了局部异常因子(LOF)之外,内部和异常值之间的决策边界以黑色显示,因为当用于异常值检测时,它没有预测方法应用于新数据。
svm.OneClassSVM被称为是对异常值敏感,并因此对异常值检测不执行的非常好。当训练集未被异常值污染时,该估计器最适合于新颖性检测。也就是说,高维中的离群检测,或者对上层数据的分布没有任何假设是非常具有挑战性的,并且单类SVM可能在这些情况下根据其超参数的值给出有用的结果。
covariance.EllipticEnvelope假设数据是高斯数据并学习椭圆。因此,当数据不是单峰时,它会降级。但请注意,此估算器对异常值很稳健。
ensemble.IsolationForest并且neighbors.LocalOutlierFactor 似乎对多模态数据集表现得相当好。neighbors.LocalOutlierFactor对于第三数据集示出了优于其他估计器的优点 ,其中两种模式具有不同的密度。这一优势可以通过LOF的局部方面来解释,这意味着它只将一个样本的异常得分与其邻居的得分进行比较。
最后,对于最后一个数据集,很难说一个样本比另一个样本更异常,因为它们均匀分布在超立方体中。除了svm.OneClassSVM稍微过度拟合之外,所有估算者都为这种情况提供了不错的解决方案。在这种情况下,更仔细地观察样本的异常分数是明智的,因为良好的估计器应该为所有样本分配相似的分数。
虽然这些例子给出了一些关于算法的直觉,但这种直觉可能不适用于非常高维的数据。
最后,请注意模型的参数已经在这里精心挑选,但实际上它们需要进行调整。在没有标记数据的情况下,问题完全没有监督,因此模型选择可能是一个挑战。
代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
import timeimport numpyas npimport matplotlibimport matplotlib.pyplotas pltfrom sklearn import svmfrom sklearn.datasets import make_blobs, make_moonsfrom sklearn.covariance import EllipticEnvelopefrom sklearn.ensemble import IsolationForestfrom sklearn.neighbors import LocalOutlierFactormatplotlib.rcParams['contour.negative_linestyle'] ='solid'# Example settingsn_samples = 300outliers_fraction = 0.15n_outliers =int(outliers_fraction * n_samples)n_inliers = n_samples - n_outliers# define outlier/ anomaly detection methods to be comparedanomaly_algorithms = [ ("Robust covariance", EllipticEnvelope(contamination=outliers_fraction)), ("One-Class SVM", svm.OneClassSVM(nu=outliers_fraction, kernel='rbf',gamma=0.1)), ("Isolation Forest", IsolationForest(behaviour='new', contamination=outliers_fraction, random_state=42)), ("Local Outlier Factor", LocalOutlierFactor(n_neighbors=35, contamination=outliers_fraction))]# define datasetsblobs_params = dict(random_state=0, n_samples=n_inliers, n_features=2)datasets = [ make_blobs(centers=[[0, 0], [0, 0]], cluster_std=0.5, **blobs_params)[0], make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[0.5, 0.5], **blobs_params)[0], make_blobs(centers=[[2, 2], [-2, -2]], cluster_std=[1.5, 0.3], **blobs_params)[0], 4. * (make_moons(n_samples=n_samples, noise=0.05, random_state=0)[0] - np.array([0.5, 0.25])), 14. * (np.random.RandomState(42).rand(n_samples, 2) - 0.5)]# Compare given classifiers under given settingsxx, yy = np.meshgrid(np.linspace(-7, 7, 150), np.linspace(-7, 7, 150))plt.figure(figsize=(len(anomaly_algorithms) * 2 + 3, 12.5))plt.subplots_adjust(left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01)plot_num = 1rng = np.random.RandomState(42)for i_dataset, Xin enumerate(datasets): # add outliers X = np.concatenate([X, rng.uniform(low=-6, high=6, size=(n_outliers, 2))], axis=0) for name, algorithmin anomaly_algorithms: print(name , algorithm) t0 = time.time() algorithm.fit(X) t1 = time.time() plt.subplot(len(datasets), len(anomaly_algorithms), plot_num) if i_dataset == 0: plt.title(name, size=18) # fit the data and tag outliers if name =='Local Outlier Factor': y_pred = algorithm.fit_predict(X) else: y_pred = algorithm.fit(X).predict(X) # plot the levels lines and the points if name !="Local Outlier Factor": Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='black') colors = np.array(["#377eb8",'#ff7f00']) plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[(y_pred + 1)// 2]) plt.xlim(-7, 7) plt.ylim(-7, 7) plt.xticks(()) plt.yticks(()) plt.text(0.99, 0.01, ('%.2fs' % (t1 - t0)).lstrip('0'), transform=plt.gca().transAxes, size=15, horizontalalignment='right') plot_num += 1plt.show() |
结果
参考文献:https://www.cnblogs.com/pinard/p/9314198.html
https://www.jianshu.com/p/5af3c66e0410
https://www.cnblogs.com/wanghui-garcia/p/11475396.html
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html



