数学 · 神经网络（一）· 前向传导
========== 2017.05.16 更新 ==========
更细致的说明可以参见这里
========== 分割线的说 ==========
神经网络的数学部分可能会让许多人望而生畏，各种梯度的计算可能也会让人有些吃力事实上……
确实如此（喂）。不过，如果静下心来好好推导一下的话，可能又会觉得它比想象中的简单
这一章我们要介绍的是算法中比较简单的前向传导算法（感谢评论区
的建议，将原翻译“前传算法”改成了“前向传导算法”），为此我们要先弄懂算法的过程。我们先来看两层之间的前向传导是怎么样的（以下除了偏置量 b 是数以外，其它变量都是矩阵）：
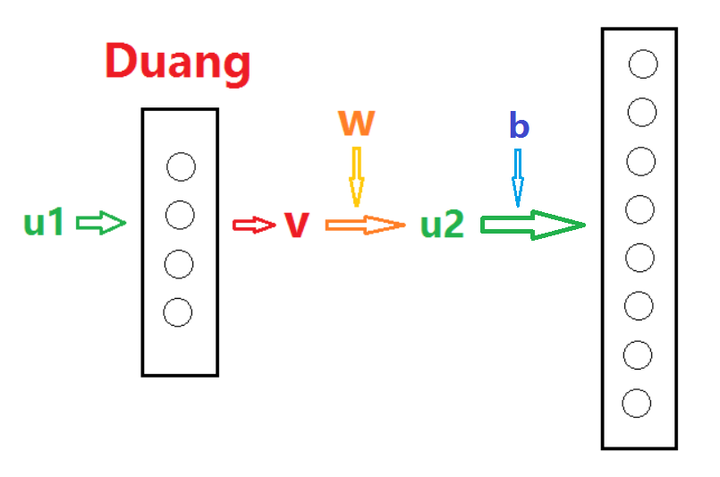大概就是这个感觉。我们再把上面的过程写成数学语言就行：
其中各个矩阵的 shape 为（是输入的数据个数）：
其中，叫做激活函数、也就是每一层自己 Duang 的部分。直观地说：
- 所谓激活函数，正是整个结构中的非线性扭曲力
也就是说，激活函数是神经网络之所以能够进行非线性扭曲的关键
那么是什么？注意到
、也就是说
是
非线性扭曲后的结果。一般来说，可以把
叫做激活值
的作用，就是将这个激活值线性映射到另一个空间上；
的作用，则是在这个基础上再进行一步平移操作
这里展开讲的会会涉及到数学分析和高等代数的相关知识，个人觉得如果不是专攻理论的话可以不太在意背后的理论基础、而如果是相关专业的话我的能力也 hold 不住 (^_^;)
以上就把两层之间的前向传导算法介绍完了。对于整个神经网络而言，只需要将上面讲的步骤不断重复进行即可
稍微总结一下：
- 输入：
的矩阵 X，其中 n 是样本个数、d 是数据维数
- 逐层进行激活，一路向前传导：
- 将输入该层的数据通过激活函数
进行非线性扭曲
- 将扭曲后的结果通过层与层之间的权重
线性映射到另一个空间上、同时可以通过偏置量
来进行一个平移
- 将最终结果传给下一层作为下一层的输入
下一章就要讲 BP（反向传播）算法了。BP 是神经网络训练的核心、推导也会稍微复杂一点，但是对于最简单的情形（梯度下降），如果按部就班地算的话、可能会发现其实不过如此
希望观众老爷们能够喜欢~
编辑于 2017-05-16
