数学 · RNN(二)· BPTT 算法
(这里是本章会用到的 GitHub 地址)
(感谢评论区
指出本文的诸多错误!!真的非常感谢!!【拜】)
RNN 的“前向传导算法”
在说明如何进行训练之前,我们先来回顾一下 RNN 的“前向传导算法。在上一章中曾经给过一个没有激活函数和变换函数的公式:
在实现层面来说,这就是一个循环的事儿,所以代码写起来会比较简单:
import numpy as np
class RNN1:
def __init__(self, u, v, w):
self._u, self._v, self._w = np.asarray(u), np.asarray(v), np.asarray(w)
self._states = None
# 激活函数
def activate(self, x):
return x
# 变换函数
def transform(self, x):
return x
def run(self, x):
output = []
x = np.atleast_2d(x)
# 初始化 States 矩阵为零矩阵
# 之所以把所有 States 记下来、是因为训练时(BPTT 算法)要用到
self._states = np.zeros([len(x)+1, self._u.shape[0]])
for t, xt in enumerate(x):
# 对着公式敲代码即可 ( σ'ω')σ
self._states[t] = self.activate(
self._u.dot(xt) + self._w.dot(self._states[t-1])
)
output.append(self.transform(
self._v.dot(self._states[t]))
)
return np.array(output)可以用上一章说过的那个小栗子来测试一下:
- 假设现在
是单位阵,
是单位阵的两倍
- 假设输入序列为:
对应的测试代码如下:
n_sample = 5
rnn = RNN1(np.eye(n_sample), np.eye(n_sample), np.eye(n_sample) * 2)
print(rnn.run(np.eye(n_sample)))程序输出为:

这和我们上一章推出的理论值是一致的(
)
RNN 的“反向传播算法”
简洁起见,我们采用上一章第一张图所示的那个朴素网络结构:
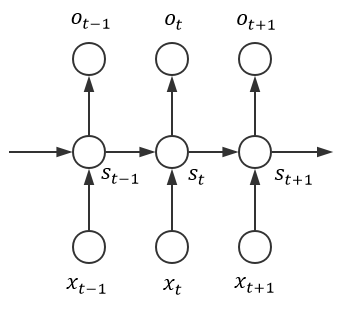
然后做出如下符号约定:
- 取
作为隐藏层的激活函数
- 取
作为输出层的变换函数
- 取
作为模型的损失函数,其中标签
是一个 one-hot 向量;由于 RNN 处理的通常是序列数据、所以在接受完序列中所有样本后再统一计算损失是合理的,此时模型的总损失可以表示为(假设输入序列长度为
):
为了更清晰地表明各个配置,我们可以整理出如下图所示的结构:
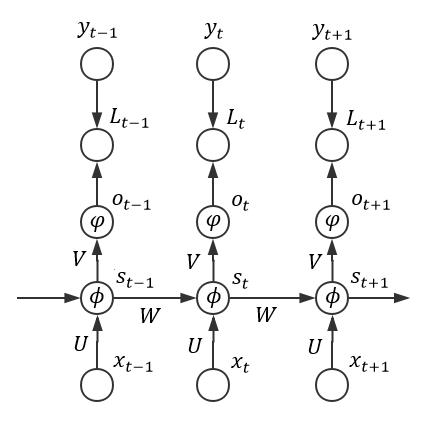
易知,其中
。令:
则有:
从而(注:统一使用“”表示 element wise 乘法,使用“
”表示矩阵乘法):
可见对矩阵的分析过程即为普通的反向传播算法,相对而言比较平凡。由
可知,它的总梯度可以表示为:
而事实上,RNN 的 BP 算法的主要难点在于它 State 之间的通信,亦即梯度除了按照空间结构传播()以外,还得沿着时间通道传播(
),这导致我们比较难将相应 RNN 的 BP 算法写成一个统一的形式(回想之前的“前向传导算法”)。为此,我们可以采用“循环”的方法来计算各个梯度
由于是反向传播算法,所以应从
开始降序循环至 1,在此期间(若需要初始化、则初始化为 0 向量或 0 矩阵):
- 计算时间通道上的“局部梯度” :
- 利用时间通道上的“局部梯度”计算
和
的梯度:
以上即为 RNN 反向传播算法的所有推导,它比 NN 的 BP 算法要繁复不少。事实上,像这种需要把梯度沿时间通道传播的 BP 算法是有一个专门的名词来描述的——Back Propagation Through Time(常简称为 BPTT,可译为“时序反向传播算法”)
不妨举一个具体的栗子来加深理解,假设:
- 激活函数
为 Sigmoid 函数
- 变换函数
为 Softmax 函数
- 损失函数
为 Cross Entropy(感谢评论区 指出这里的错误):
由 NN 处的讨论可知这是一个非常经典、有效的配置,其中:
从而
且从
开始降序循环至 1 的期间中,各个“局部梯度”为:
由此可算出如下相应梯度:
可以看到形式相当简洁,所以我们完全可以比较轻易地写出相应实现:
class RNN2(RNN1):
# 定义 Sigmoid 激活函数
def activate(self, x):
return 1 / (1 + np.exp(-x))
# 定义 Softmax 变换函数
def transform(self, x):
safe_exp = np.exp(x - np.max(x))
return safe_exp / np.sum(safe_exp)
def bptt(self, x, y):
x, y, n = np.asarray(x), np.asarray(y), len(y)
# 获得各个输出,同时计算好各个 State
o = self.run(x)
# 照着公式敲即可 ( σ'ω')σ
dis = o - y
dv = dis.T.dot(self._states[:-1])
du = np.zeros_like(self._u)
dw = np.zeros_like(self._w)
for t in range(n-1, -1, -1):
st = self._states[t]
ds = self._v.T.dot(dis[t]) * st * (1 - st)
# 这里额外设定了最多往回看 10 步
for bptt_step in range(t, max(-1, t-10), -1):
du += np.outer(ds, x[bptt_step])
dw += np.outer(ds, self._states[bptt_step-1])
st = self._states[bptt_step-1]
ds 

