Metric Learning——度量学习
看到一篇知乎大神Flood Sung发表在CVPR2018上的paper,介绍了一种基于metric的模式识别方法,创新之处在于它不同于常用的matric-based方法,使用人为定义的度量,像简单的欧式距离、马氏距离,而是采用了用神经网络去训练这个度量,模型虽然简单,但是效果却很显著。
1、度量(Metric)
先说一下关于度量这个概念:在数学中,一个度量(或距离函数)是一个定义集合中元素之间距离的函数。一个具有度量的集合被称为度量空间。
2、度量学习的作用
度量学习也叫作相似度学习,根据这个叫法作用就很明确了。
之所以要进行度量学习,一方面在一些算法中需要依赖给定的度量:如Kmeans在进行聚类的时候就用到了欧式距离来计算样本点到中心的距离、KNN算法也用到了欧式距离等。这里计算的度量,就是比较样本点与中心点的相似度。
这里的度量学习在模式识别领域,尤其是在图像识别这方面,在比较两张图片是否是相同的物体,就通过比较两张图片的相似度,相似度大可能性就高。
因为在研究时间序列这方面的问题,所以想到了在时间序列中度量学习的体现,如果是判断两个区间的相似性,通常用到的度量方式就是采用常用到的欧式或者其他人为定义的距离函数,这样也就局限于了这样一个二维或者多维的空间中,而如果是用到Flood Sung大神提出的方法的话,我们把思路拓宽,能不能也是用神经网络来训练这个度量,这样的好处就是:
- 长度不同的片段也可以进行比较。
- 可以拓宽维度,从其他维度上寻找关联。
以下摘自:https://blog.csdn.net/nehemiah_li/article/details/44230053
3、常用到的度量学习方法
从广义上将度量学习分为:通过线性变换的度量学习和度量学习的非线性模型。
3.1线性变换的度量学习
线性的度量学习问题也称为马氏度量学习问题,可以分为监督的和非监督的学习算法。
3.1.1监督的全局度量学习
- Information-theoretic metric learning(ITML)
- Mahalanobis Metric Learning for Clustering(MMC)
- Maximally Collapsing Metric Learning (MCML)
3.1.2监督的局部度量学习
- Neighbourhood Components Analysis (NCA)
- Large-Margin Nearest Neighbors (LMNN)
- Relevant Component Analysis(RCA)
- Local Linear Discriminative Analysis(Local LDA)
3.1.3非监督的度量学习
- 主成分分析(Pricipal Components Analysis, PCA)
- 多维尺度变换(Multi-dimensional Scaling, MDS)
- 非负矩阵分解(Non-negative Matrix Factorization,NMF)
- 独立成分分析(Independent components analysis, ICA)
- 邻域保持嵌入(Neighborhood Preserving Embedding,NPE)
- 局部保留投影(Locality Preserving Projections. LPP)
3.2度量学习的非线性模型
非线性降维算法可以看作属于非线性度量学习:
- 等距映射(Isometric Mapping,ISOMAP)
- 局部线性嵌入(Locally Linear Embedding, LLE)
- 拉普拉斯特征映射(Laplacian Eigenmap,LE )
通过核方法来对线性映射进行扩展:
- Non-Mahalanobis Local Distance Functions
- Mahalanobis Local Distance Functions
- Metric Learning with Neural Networks
4、论文推荐
- Distance metric learning with application to clustering with side-information
- Information-theoretic metric learning(关于ITML)
- Distance metric learning for large margin nearest neighbor classification(关于LMNN)
- Learning the parts of objects by non-negative matrix factorization(Nature关于RCA的文章)
- Neighbourhood components analysis(关于NCA)
- Metric Learning by Collapsing Classes(关于MCML)
- Distance metric learning a comprehensive survey(一篇经典的综述)
个人总结
想了一下,度量学习定位的话应该是最基础的部分。现在在用的无论是深度学习、强化学习还是神经网络或是监督学习,为了避免结果发散或者收敛结果好些,在使用前一般需要一个特征转换或者聚类的处理,在进行特征转换或者聚类时最基本的和最容易忽略的部分就是关于度量的学习,使用人为定义的方法必然有其局限性,那么通过神经网络或者其他方法是否效果会更好呢,将这个可以进一步研究。
《Discriminative Deep Metric Learning for Face Verification in the Wild》阅读记录
简介
度量学习(Metric Learning)也就是常说的相似度学习。如果需要计算两张图片之间的相似度,如何度量图片之间的相似度使得不同类别的图片相似度小而相同类别的图片相似度大(maximize the inter-class variations and minimize the intra-class variations)就是度量学习的目标。
例如如果我们的目标是识别人脸,那么就需要构建一个距离函数去强化合适的特征(如发色,脸型等);而如果我们的目标是识别姿势,那么就需要构建一个捕获姿势相似度的距离函数。为了处理各种各样的特征相似度,我们可以在特定的任务通过选择合适的特征并手动构建距离函数。然而这种方法会需要很大的人工投入,也可能对数据的改变非常不鲁棒。度量学习作为一个理想的替代,可以根据不同的任务来自主学习出针对某个特定任务的度量距离函数。
conventional Mahalanobis distance metric learning
传统马氏距离度量学习是从训练集XX中寻找矩阵M∈Rd×dM∈Rd×d,计算两个样本x1x1,x2x2之间的马氏距离:
dM(xi,xj)=(xi−xj)TM(xi−xj)−−−−−−−−−−−−−−−−−√dM(xi,xj)=(xi−xj)TM(xi−xj)
由于MM为对称半正定矩阵,因此可以分解为:
M=WTWM=WTW
其中W∈Rp×d,p<dW∈Rp×d,p<d 。那么:
dM(xi,xj)=(xi−xj)TWTW(xi−xj)−−−−−−−−−−−−−−−−−−−−√=∥Wxi−Wxj∥2dM(xi,xj)=(xi−xj)TWTW(xi−xj)=‖Wxi−Wxj‖2
根据上面公式可知传统的马氏距离度量学习是通过寻找一个线性转换将每一个样本xixi投影到低维子空间中(因为 p<dp<d),投影后样本间的欧式距离即为原空间中的马氏距离。
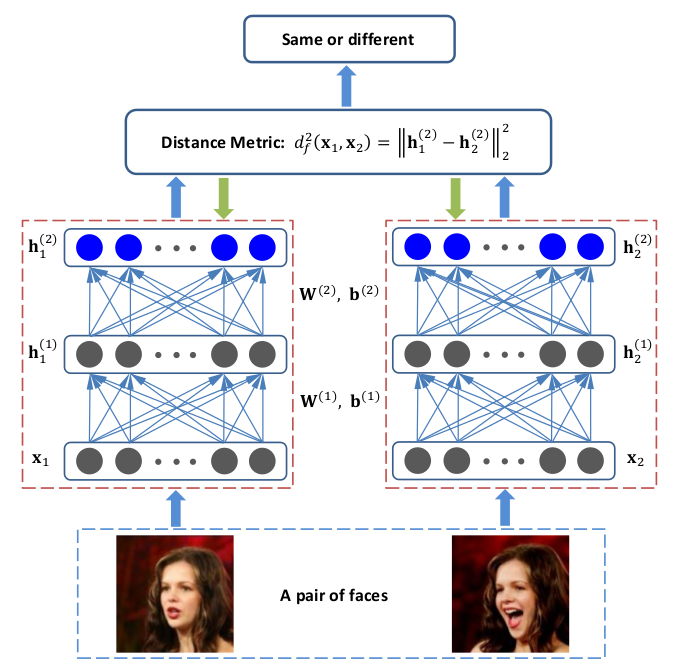
discriminative deep metric learning (DDML)
由于传统方法用到的线性变换不能够捕捉面部图片所依赖的非线性流形(nonlinear manifold)
线性流型
几何空间的直线或平面具有性质:集合中任意2点生成的直线一定包含在这个集合里,即直线和平面是平和直的。把平和直的概念推广到高维就能得到线性流形的概念。
为了解决传统方法的限制,论文提到将样本投影到高维特征空间中,在高维空间中进行距离度量。
度量学习之论文参考
2018.07.24 22:53 142浏览
字号
一. 传统的距离度量学习方法:
监督方法
1.NIPS 2005(LMNN):Distance Metric Learning for Large Margin Nearest Neighbor Classification
1.1 AAAI 2017(LMNN的拓展):Parameter Free Large Margin Nearest Neighbor for Distance Metric Learning
2. Lecture Notes(FLD(LDA的一种),必看):Fisher Linear Discriminant Analysis(FLD)
2.1 NIPS 2003(MMC,解决了LDA样本少出现不可逆的问题):Efficient and Robust Feature Extraction by Maximum Margin Criterion
2.2 CVPR 2007(ANMM,注意与LDA的关系以及与MMC,LMNN的区别联系):Feature Extraction by Maximizing the Average Neighborhood Margin
2.3 ICCV 2005(SNMMC,同样是解决LDA出现的四大问题,逐步的思想以及margin的设定很不错):Face Recognition By Stepwise Nonparametric Margin Maximum Criterion
2.4 ECML 2004(MMDA,将分类器与数据降维特征提取结合,非常棒的发现):Margin Maximizing Discriminant Analysis
3.NIPS 2009(相似度学习(Similarity Learning),放弃了对称和半定的约束,但实验效果也不变差,建议看一下):An Online Algorithm for Large Scale Image Similarity Learning
无监督方法:
1.Lecture Notes(PCA,必看):Principal Component Analysis(PCA)
二. 深度距离度量学习:
1.CVPR 2014: Discriminative Deep Metric Learning for Face Verification in the Wild
2.CVPR 2015(注意与1的区别与联系):Multi-Manifold Deep Metric Learning for Image Set Classification
3.CVPR 2016(最大化使用batch)Deep Metric Learning via Lifted Structured Feature Embedding
4.NIPS 2016(注意与3的区别)Improved Deep Metric Learning with Multi-class N-pair Loss Objective
三. 辅助论文学习(上述距离度量论文中涉及的内容):
1.CVPR2016(近似近邻搜索): FANNG: Fast Approximate Nearest Neighbour Graphs
基于深度学习的Person Re-ID(度量学习)
度量学习 是指 距离度量学习,Distance Metric Learning,简称为 DML,做过人脸识别的童鞋想必对这个概念不陌生,度量学习是Eric Xing在NIPS 2002提出。
这并不是个新词,说的直白一点,metric learning 是通过特征变换得到特征子空间,通过使用度量学习,让类似的目标距离更近(PULL),不同的目标距离更远(push),也就是说,度量学习需要得到目标的某些核心特征(特点),比如区分两个人,2只眼睛1个鼻子-这是共性,柳叶弯眉樱桃口-这是特点。
我们可以把 度量学习分为两种,一种是基于监督学习的,另外一种是基于非监督学习的。
一. 监督学习
1)LDA Fisher线性判别
2)Local LDA
Local Linear Discriminative Analysis
3)RCA 相关成分分析
Relevant Component Analysis
4)LPP 局部保留投影
Locality Preserving Projection
5)LMNN 大间隔最近邻
Large-Margin Nearest Neighbors
6)LLE 局部线性嵌入
Locally linear embedding
监督学习的方法应用比较多,包括上一节我们讲到的 基于CNN的特征提取都属于监督学习的范畴。
二. 非监督学习
严格说来,非监督的度量学习(主要是指降维方法)不算真正的度量学习,我们也把他们列出来,方便读者记忆:
1)主成分分析(Pricipal Components Analysis, PCA)
2)多维尺度变换(Multi-dimensional Scaling, MDS)
3)独立成分分析(Independent components analysis, ICA)
4)拉普拉斯特征映射(Laplacian Eigenmaps)
ok,就讲到这里,剩下的需要大家具体了解每一个方法,然后提出自己的新方法!