【P2P网络中的声誉计算】The EigenTrust Algorithm for Reputation Management in P2P Networks
【学习的文章】The EigenTrust Algorithm for Reputation Management in P2P Networks
发表会议:WWW2003
作者:Kamvar S D , Schlosser M T , Garcia-Molina H
单位:Stanford University
【摘要】这篇文献提出来的一种名为EigenTrust的信誉系统,旨在减少Peer-to-peer文件共享网络中不真实文件的下载次数,该算法能够根据peer端的上传历史为每个端点分配唯一的全局信任值。这篇文献提出了一种基于Power迭代的分布式安全方法来计算这个全局信任值,通过让Peer端使用这个全局信任值来选择其想要下载的对口Peer个体,网络可以有效地识别恶意Peer并将其与网络隔离。通过仿真计算,即便在存在恶意个体们联合破坏系统的情况下,EigenTrust信誉系统也能明显减少网络上不真实文件的数量。
Peer-to-peer 文件共享网络相比传统的客户端-服务器的网络在数据分发上有许多明显优势,包括鲁棒性、可伸缩性和可用数据的多样性等等。但另一方面,由于Peer-to-peer 文件共享网络的开放性和匿名性特点,网络上的Peer端个体无需对其放在网络上的文件负责任,于是导致了一些恶意攻击行为,例如病毒文件、钓鱼文件等等。
EigenTrust的信誉系统为每个peer i 分配一个唯一的全局信任值,该值反映了在与 i 有关联的网络中所有peer的体验。这个全局信任值是通过网络中的所有peer 以分布式和节点对称的方式参与计算的,但同时能保证整个网络上的开销能达到最小。另外,文章还描述了如何确保计算的安全性,从而最大程度地降低了系统中恶意peer进行欺诈的可能性。
1 EigenTrust信誉系统设计上的几点考虑
这里提到了五点要求:
- 该系统应具有自我监管的能力(self-policing)。也就是说,用户群体的遵循的规矩是由群体共同定义和执行的,而没有某个中央监管机构。
- 系统应具备匿名性。也就是说,某个peer i 的信誉应该是与系统网络里一些不透明的标识符信息(例如peer的Gnutella用户名)关联,而不是系统外的信息(例如peer的IP地址)。
- 信誉等评价指标对新成员没有好处。也就是说,peer应该通过群体种的多次交易并保持一致的良好行为来获得信誉,而信誉不佳的恶意peer即便不断更改其系统中的不透明标识符以获取新来者身份也不应该有任何好处。
- 就计算、基础架构、存储和信息的复杂程度而言,信誉系统在计算信誉时应考虑最小的开销。
- 系统对恶意的实体应有很强的抵抗力。系统中的peer对于试图滥用系统的恶意用户应立即在系统中识别并阻止。
后来学界公认一个完整的信誉系统所必备的几个要点时除上述外,还加了一条:网络中的实体能够经得住时间的考验,也就是说,存在时间会很长,当前发生相互作用之后,通常假定将来会发生后续相互作用,这些实体不会消失。
2 信誉系统
举一个典型的信誉管理系统:在线拍卖系统eBay。在eBay的信誉系统中,买卖双方都可以在每次交易后相互评分,而参与者的总体信誉是过去6个月中这些评分的总和,而该系统依靠的是集中式系统来存储和管理这些评分。
借鉴eBay这种评分模式,在peer-to-peer文件传输系统中,也可以建立类似的评分。例如,每当peer i 从peer j 处下载文件时,可以对文件质量评级为正( )或负(
),如果下载的文件不真实、被篡改,或是下载被中断,peer i就可能对此打负的评分。由此,我们可以对 j 定义一个来自 i 的本地信任值:
. 在这同时,在 i 那一端,也会存储一个与对 j 的满意度相关的一个值:
在这篇文章提出来之前的研究工作里,peer-to-peer信誉系统中大多基于这种本地信任值的概念。但是,在分布式环境中,这会面临一个问题:要么对某个peer的信任值只通过几个它相关的peer端的本地信任值进行整合,无法合成它的全局信任值;要么就只能向全局所有的peer端查询,这样会阻塞网络。
这篇文章提出了一种新的信誉系统,它以自然的方式聚集所有用户的本地信任值,在信息复杂度方面具有最小开销。基于传递信任的概念:peer i 会对那些提供真实文件的peer有很高的评价。此外,peer i可能会信任那些他评价高的peer的意见,认为这些提高真实文件的peer时诚实的,会如实报告他们的本地信任值。更好的是,这种信任传递的思想可以推导出一个很好的结论:全局信任值对应于规范化的局部信任值矩阵的左主特征向量,而且这种算法的计算复杂度不高。下面将详细说明。
3 EigenTrust信誉系统
本节的内容主要包括:
- 如何规范化局部信任值
- 如何以合理的方式整合规范化的局部信任值
- 如何对局部和全局信任值进行概率解释
- 这个算法的实现
3.1 规范化局部信任值
将局部信任值规范化的主要目的是避免恶意节点之间互相打高分。通常,可以定义规范化后的局部信任值(local trust value): (1)
该式确保了所有的 都在0到1之间,但值得注意的是当
时
没有意义,这个问题后面会说到。另外,这种简单的规范化还有两个不足:
- 无法将那些与”我“没有交互的peer或者经验很不足的peer给的评分区分出来。
是个相对值,没有表示绝对的度量。就是说,当
时,我们可以知道 j 和 k 在 i 眼里有同样的信誉,但我们不知道他们是同等的值得信任还是同等的不可信。
但这篇文章指出,尽管存在这些缺陷,以这样的方式进行规范化仍取得了良好的效果。
3.2 整合局部信任值
为了有效计算,采取一种自然的想法:在分布式环境中,一种获取得到全局信任值的办法就是让peer向其熟人询问对其他peer的看法。即,i 向他的熟人询问得到 k 是否值得信任:
该式可以通过矩阵C表示 , 即
.
这是一种很有用的方法,可以让 i 获得比自己的经验更广泛的网络视图,但仅限于 i 自己和他朋友的经验视野。为了让范围更广,i 可以询问朋友的朋友,以此类推,即 . 当n很大时,迭代n次,i 即可以获取全局视野。并且,好的是,当n很大时,信任值向量
对于每一个节点i都会收敛到相当的向量。也就是说,t 可以构成一个全局信任向量,而向量
可以量化整个系统对 j 的信任程度。
3.3 概率解释
上述模型也可以用Random Surfer Model 简单理解:如果某个agent想要探索到信誉良好的peer,那么他可以使用如下规则来进行全网搜索:在每个端点 i,他以 的概率走到 j 处去。当这样的搜索进行一段时间以后,那么这个agent所游走到的节点更可能是信誉良好的断点。那么,由矩阵 C 定义的 马尔科夫链的平稳分布 就是这个agent想要找的全局信任值。
3.4 Basic EigenTrust
先暂时忽略分布式,假设某个中心服务器知道所有的 的值并进行计算,如下图所示。

3.5 实际的EigenTrust
前述基本EigenTrust提出的简单算法没有解决三个实际问题:关于信任的先验经验、非活动peer端和恶意peer。
- 信任的先验经验(A priori notions of trust)
在Peer-to-peer文件共享网络中,是有一些先验经验的。例如,我们可以认为最初加入网络的少数peer通常是可信的,因为p2p网络的设计者和早期用户可能没有太大的动机来破坏他们构建的网络。这样,我们可以通过这些预先就信任的peer定义分布 。例如,集合P里的peer被认为是可靠的,我们可以定义
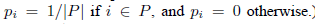
分布 可以用在三个地方:
- 存在恶意peer个体的情况下,通常
收敛地比
要快,因此我们通常可以使用
作为初始的向量。
- 存在不活跃peer的情况下,即 i不从任何人那里下载文件,那么根据(1)式cij就没有意义。在这种情况下,我们可以定义
.就是说,如果 i 不认识或不信任任何人,i 就选择信任那些被预先信任的人。
- 存在恶意peer集体的情况下,我们使用下式来减少集体作案的影响。让集体中每个断点都必须选择一定的概率a相信那些被预先信任的人。从概率上,前面在网络中进行探索的agent不太可能在游走进恶意集合时陷入困境,因为在每一步,他都有一定的概率爬网到预先信任的peer。另外,这种算法也使得矩阵C是非奇异的和非周期的,保证了计算的收敛性。
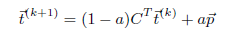
改进后的EigenTrust实用算法流程图如下:

3. 6 分布式的 EigenTrust算法
- 这个分布式算法,在网络中所有的peer合作计算和存储全局信任向量,并且每个节点的计算、存储和交互开销都是最小的。
在分布式环境中,第一个挑战就是如何存在向量C 和 t . 先不考虑安全性的问题,每个peer按下式计算各自的全部信任值:
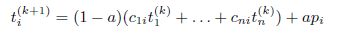
显然上式的矩阵C是稀疏的(因为与i有交互的节点有限)

3.7 算法复杂性
该算法的复杂程度是有上界的,主要是基于:
- 算法收敛速度快。
- 可以特别限制peer报告的局部信任值的数量。
4 考虑安全的EigenTrust算法
在安全性问题的考虑上,这个算法主要通过两个基本思想来解决。
- peer i 的当前信任值不能由它计算和保存,因为单个peer本身很容易受到操纵。因此,我们在网络中选择另外一个peer来计算i的信任值。
- 当通过恶意的peer j 计算任何一个peer的信任值时,将按 j 的意愿返回错误的结果。因此,网络中一个peer的信任值将由多个peer来共同计算。
5 Threat models
通过恶意peer的策略建立了几种模型来测试文章提出的信誉系统,结果都挺好的~
(差不多学习完毕....)



