梯度下降算法原理讲解——机器学习

博文目录

 

1. 概述

梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。
本文将从一个下山的场景开始，先提出梯度下降算法的基本思想，进而从数学上解释梯度下降算法的原理，解释为什么要用梯度，最后实现一个简单的梯度下降算法的实例！

2. 梯度下降算法

2.1 场景假设

梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了
在这里插入图片描述

2.2 梯度下降

梯度下降的基本过程就和下山的场景很类似。

首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢？接下来，我们从微分开始讲起：

2.2.1 微分

看待微分的意义，可以有不同的角度，最常用的两种是：

  • 函数图像中，某点的切线的斜率
  • 函数的变化率
    几个微分的例子：

1.单变量的微分，函数只有一个变量时

d ( x 2 ) d x = 2 x \frac{d(x^2)}{dx}=2xdxd(x2)​=2x

d ( − 2 y 5 ) d y = − 10 y 4 \frac{d(-2y^5)}{dy}=-10y^4dyd(−2y5)​=−10y4

d ( 5 − θ ) 2 d θ = − 2 ( 5 − θ ) \frac{d(5-\theta )^2}{d\theta}=-2(5-\theta)dθd(5−θ)2​=−2(5−θ)

2.多变量的微分，当函数有多个变量的时候，即分别对每个变量进行求微分

∂ ∂ x ( x 2 y 2 ) = 2 x y 2 \frac{\partial}{\partial x}(x^2y^2) = 2xy^2∂x∂​(x2y2)=2xy2

∂ ∂ y ( − 2 y 5 + z 2 ) = − 10 y 4 \frac{\partial}{\partial y}(-2y^5+z^2) = -10y^4∂y∂​(−2y5+z2)=−10y4

∂ ∂ θ 2 ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) = 2 \frac{\partial}{\partial \theta_{2}}(5\theta_{1} + 2\theta_{2} - 12\theta_{3}) = 2∂θ2​∂​(5θ1​+2θ2​−12θ3​)=2

∂ ∂ θ 2 ( 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ) = − 2 \frac{\partial}{\partial \theta_{2}}(0.55 - (5\theta_{1} + 2\theta_{2} - 12\theta_{3})) = -2∂θ2​∂​(0.55−(5θ1​+2θ2​−12θ3​))=−2

2.2.2 梯度

梯度实际上就是多变量微分的一般化。
下面这个例子：

J ( Θ ) = 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) J(\Theta ) = 0.55 - (5\theta_{1} + 2\theta_{2} - 12\theta_{3})J(Θ)=0.55−(5θ1​+2θ2​−12θ3​)

▽ J ( Θ ) = < ∂ J ∂ θ 1 , ∂ J ∂ θ 2 , ∂ J ∂ θ 3 > = ( − 5 , − 2 , 12 ) \triangledown J(\Theta ) = \left < \frac{\partial J}{\partial \theta_{1}}, \frac{\partial J}{\partial \theta_{2}},\frac{\partial J}{\partial \theta_{3}} \right > =(-5,-2,12)▽J(Θ)=⟨∂θ1​∂J​,∂θ2​∂J​,∂θ3​∂J​⟩=(−5,−2,12)

我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实一个向量。

梯度是微积分中一个很重要的概念，之前提到过梯度的意义

  • 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
  • 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

2.3 数学解释

首先给出数学公式：

Θ 1 = Θ 0 + α ▽ J ( Θ ) → e v a l u a t e d a t Θ 0 {\color{Red} \Theta^1} = {\color{Blue} \Theta^0} + {\color{Green} \alpha} {\color{Purple} \triangledown J(\Theta)}\rightarrow evaluated at \Theta^0Θ1=Θ0+α▽J(Θ)→evaluatedatΘ0

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点！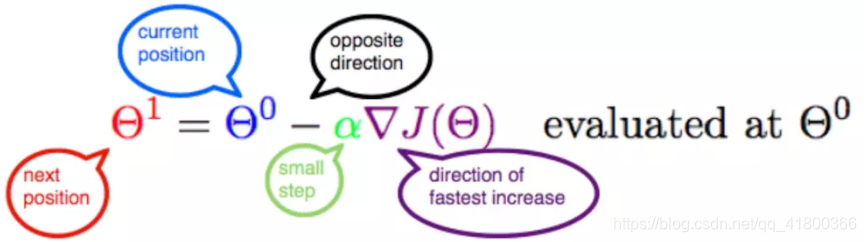
在这里插入图片描述

2.3.1 α

α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大扯着蛋，哈哈，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

2.3.2 梯度要乘以一个负号

梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号；那么如果时上坡，也就是梯度上升算法，当然就不需要添加负号了。

3. 实例

我们已经基本了解了梯度下降算法的计算过程，那么我们就来看几个梯度下降算法的小实例，首先从单变量的函数开始，然后介绍多变量的函数。

3.1 单变量函数的梯度下降

我们假设有一个单变量的函数

J ( θ ) = θ 2 J(\theta) = \theta^2J(θ)=θ2

函数的微分，直接求导就可以得到

J ′ ( θ ) = 2 θ J'(\theta) = 2\thetaJ′(θ)=2θ

初始化，也就是起点，起点可以随意的设置，这里设置为1

θ 0 = 1 \theta^0 = 1θ0=1

学习率也可以随意的设置，这里设置为0.4

α = 0.4 \alpha = 0.4α=0.4

根据梯度下降的计算公式

Θ 1 = Θ 0 + α ▽ J ( Θ ) → e v a l u a t e d a t Θ 0 {\color{Red} \Theta^1} = {\color{Blue} \Theta^0} + {\color{Green} \alpha} {\color{Purple} \triangledown J(\Theta)}\rightarrow evaluated at \Theta^0Θ1=Θ0+α▽J(Θ)→evaluatedatΘ0

我们开始进行梯度下降的迭代计算过程：

θ 0 = 1 \theta^0 = 1θ0=1

θ 1 = θ 0 − α ∗ J ′ ( θ 0 ) = 1 − 0.4 ∗ 2 = 0.2 \theta^1 = \theta^0 - \alpha*J'(\theta^0)=1 - 0.4*2 = 0.2θ1=θ0−α∗J′(θ0)=1−0.4∗2=0.2

θ 2 = θ 1 − α ∗ J ′ ( θ 1 ) = 0.2 − 0.4 ∗ 0.4 = 0.04 \theta^2 = \theta^1 - \alpha*J'(\theta^1)= 0.2 - 0.4*0.4=0.04θ2=θ1−α∗J′(θ1)=0.2−0.4∗0.4=0.04

θ 3 = 0.008 \theta^3 = 0.008θ3=0.008

θ 4 = 0.0016 \theta^4 = 0.0016θ4=0.0016

如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底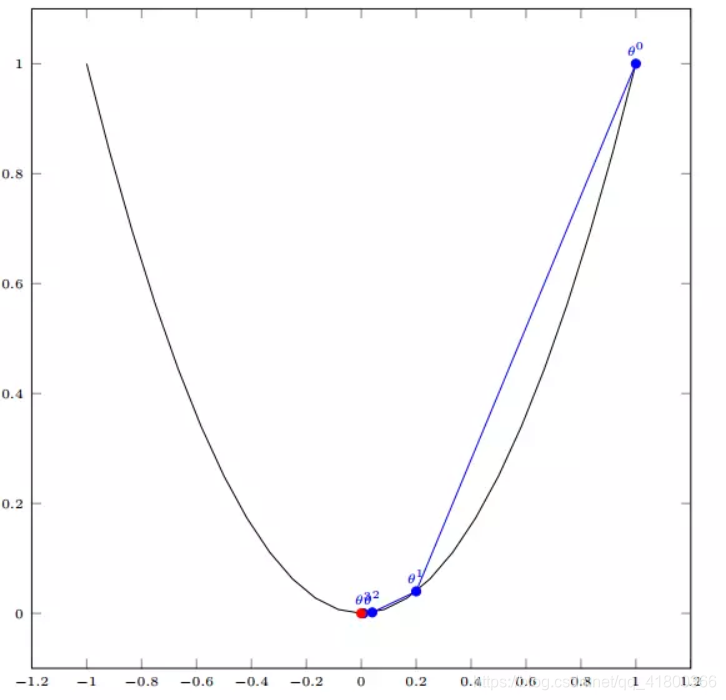
在这里插入图片描述

3.2 多变量函数的梯度下降

我们假设有一个目标函数

J ( Θ ) = θ 1 2 + θ 2 2 J(\Theta) = \theta_{1}^2 + \theta_{2}^2J(Θ)=θ12​+θ22​

现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。但是接下来，我们会从梯度下降算法开始一步步计算到这个最小值！
我们假设初始的起点为：

Θ 0 = ( 1 , 3 ) \Theta^0 = (1, 3)Θ0=(1,3)

初始的学习率为：

α = 0.1 \alpha = 0.1α=0.1

函数的梯度为：

▽ J ( Θ ) = < 2 θ 1 , 2 θ 2 > \triangledown J(\Theta ) = \left < 2\theta_{1},2\theta_{2} \right >▽J(Θ)=⟨2θ1​,2θ2​⟩

进行多次迭代：

Θ 0 = ( 1 , 3 ) \Theta^0 = (1, 3)Θ0=(1,3)

Θ 1 = Θ 0 − α ▽ J ( Θ ) = ( 1 , 3 ) − 0.1 ∗ ( 2 , 6 ) = ( 0.8 , 2.4 ) \Theta^1 = \Theta^0 - \alpha\triangledown J(\Theta ) = (1,3) - 0.1*(2, 6)=(0.8, 2.4)Θ1=Θ0−α▽J(Θ)=(1,3)−0.1∗(2,6)=(0.8,2.4)

Θ 2 = ( 0.8 , 2.4 ) − 0.1 ∗ ( 1.6 , 4.8 ) = ( 0.64 , 1.92 ) \Theta^2 = (0.8, 2.4) - 0.1*(1.6, 4.8)=(0.64, 1.92)Θ2=(0.8,2.4)−0.1∗(1.6,4.8)=(0.64,1.92)

Θ 3 = ( 0.5124 , 1.536 ) \Theta^3 =(0.5124, 1.536)Θ3=(0.5124,1.536)

Θ 4 = ( 0.4096 , 1.228800000000001 ) \Theta^4 =(0.4096, 1.228800000000001)Θ4=(0.4096,1.228800000000001)
⋮ \vdots⋮
Θ 10 = ( 0.1073741824000003 , 0.32212254720000005 ) \Theta^{10} =(0.1073741824000003, 0.32212254720000005)Θ10=(0.1073741824000003,0.32212254720000005)
⋮ \vdots⋮
Θ 50 = ( 1.141798154164342 e − 05 , 3.42539442494306 e − 05 ) \Theta^{50} =(1.141798154164342e^{-05}, 3.42539442494306e^{-05})Θ50=(1.141798154164342e−05,3.42539442494306e−05)
⋮ \vdots⋮
Θ 100 = ( 1.6296287810675902 e − 10 , 4.8888886343202771 e − 10 ) \Theta^{100} =(1.6296287810675902e^{-10}, 4.8888886343202771e^{-10})Θ100=(1.6296287810675902e−10,4.8888886343202771e−10)

我们发现，已经基本靠近函数的最小值点
在这里插入图片描述

4. 代码实现

4. 1 场景分析

下面我们将用python实现一个简单的梯度下降算法。场景是一个简单的线性回归的例子：假设现在我们有一系列的点，如下图所示：
在这里插入图片描述
我们将用梯度下降法来拟合出这条直线！

首先，我们需要定义一个代价函数，在此我们选用均方误差代价函数（也称平方误差代价函数）

J ( Θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\Theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2J(Θ)=2m1​∑i=1m​(hθ​(x(i))−y(i))2

此公式中

  • m是数据集中数据点的个数，也就是样本数
  • ½是一个常量，这样是为了在求梯度的时候，二次方乘下来的2就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
  • y 是数据集中每个点的真实y坐标的值，也就是类标签
  • h 是我们的预测函数（假设函数），根据每一个输入x，根据Θ 计算得到预测的y值，即

h Θ ( x ( i ) ) = Θ 0 + Θ 1 x 1 ( i ) h_{\Theta}(x^{(i)}) = \Theta_{0} + \Theta_{1}x_{1}^{(i)}hΘ​(x(i))=Θ0​+Θ1​x1(i)​

我们可以根据代价函数看到，代价函数中的变量有两个，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分

▽ J ( Θ ) = < δ J δ Θ 0 , δ J δ Θ 1 > \triangledown J(\Theta ) = \left < \frac{\delta J}{\delta \Theta_{0}}, \frac{\delta J}{\delta \Theta_{1}} \right >▽J(Θ)=⟨δΘ0​δJ​,δΘ1​δJ​⟩

δ J δ Θ 0 = 1 m ∑ i = 1 m ( h Θ ( x ( i ) ) − y ( i ) ) \frac{\delta J}{\delta \Theta_{0}} = \frac{1}{m}\sum_{i=1}^{m}(h_{\Theta}(x^{(i)})-y^{(i)})δΘ0​δJ​=m1​∑i=1m​(hΘ​(x(i))−y(i))

δ J δ Θ 1 = 1 m ∑ i = 1 m ( h Θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) \frac{\delta J}{\delta \Theta_{1}} = \frac{1}{m}\sum_{i=1}^{m}(h_{\Theta}(x^{(i)})-y^{(i)})x_{1}^{(i)}δΘ1​δJ​=m1​∑i=1m​(hΘ​(x(i))−y(i))x1(i)​

明确了代价函数和梯度，以及预测的函数形式。我们就可以开始编写代码了。但在这之前，需要说明一点，就是为了方便代码的编写，我们会将所有的公式都转换为矩阵的形式，python中计算矩阵是非常方便的，同时代码也会变得非常的简洁。
为了转换为矩阵的计算，我们观察到预测函数的形式

h Θ ( x ( i ) ) = Θ 0 + Θ 1 x ( i ) h_{\Theta}(x^{(i)}) = \Theta_{0} + \Theta_{1}x^{(i)}hΘ​(x(i))=Θ0​+Θ1​x(i)

我们有两个变量，为了对这个公式进行矩阵化，我们可以给每一个点x增加一维，这一维的值固定为1，这一维将会乘到Θ0上。这样就方便我们统一矩阵化的计算

( x 1 ( i ) , y ( i ) ) → ( x 0 ( i ) , x 1 ( i ) , y ( i ) ) w i t h x 0 ( i ) = 1 ∀ i (x_{1}^{(i)},y^{(i)})\rightarrow (x_{0}^{(i)},x_{1}^{(i)},y^{(i)}) with x_{0}^{(i)} = 1 \forall _{i}(x1(i)​,y(i))→(x0(i)​,x1(i)​,y(i))withx0(i)​=1∀i​

然后我们将代价函数和梯度转化为矩阵向量相乘的形式

J ( Θ ) = 1 2 m ( X Θ − y ⃗ ) T ( X Θ − y ⃗ ) J(\Theta) = \frac{1}{2m}(X\Theta - \vec{y})^{T}(X\Theta - \vec{y})J(Θ)=2m1​(XΘ−y​)T(XΘ−y​)

▽ J ( Θ ) = 1 m X T ( X Θ − y ⃗ ) ) \triangledown J(\Theta) = \frac{1}{m}X^{T}(X\Theta - \vec{y}))▽J(Θ)=m1​XT(XΘ−y​))

4. 2 代码

首先，我们需要定义数据集和学习率

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2019/1/21 21:06
# @Author  : Arrow and Bullet
# @FileName: gradient_descent.py
# @Software: PyCharm
# @Blog    ：https://blog.csdn.net/qq_41800366

from numpy import *

# 数据集大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1))  # 生成一个m行1列的向量，也就是x0，全是1
X1 = arange(1, m+1).reshape(m, 1)  # 生成一个m行1列的向量，也就是x1，从1到m
X = hstack((X0, X1))  # 按照列堆叠形成数组，其实就是样本数据
# 对应的y坐标
y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23

接下来我们以矩阵向量的形式定义代价函数和代价函数的梯度

# 定义代价函数
def cost_function(theta, X, Y):
    diff = dot(X, theta) - Y  # dot() 数组需要像矩阵那样相乘，就需要用到dot()
    return (1/(2*m)) * dot(diff.transpose(), diff)


# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
    diff = dot(X, theta) - Y
    return (1/m) * dot(X.transpose(), diff)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

最后就是算法的核心部分，梯度下降迭代计算

# 梯度下降迭代
def gradient_descent(X, Y, alpha):
    theta = array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, Y)
    while not all(abs(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, Y)
    return theta


optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

当梯度小于1e-5时，说明已经进入了比较平滑的状态，类似于山谷的状态，这时候再继续迭代效果也不大了，所以这个时候可以退出循环！
运行代码，计算得到的结果如下：

print('optimal:', optimal)  # 结果 [[0.51583286][0.96992163]]
print('cost function:', cost_function(optimal, X, Y)[0][0])  # 1.014962406233101
  • 1
  • 2

通过matplotlib画出图像，

# 根据数据画出对应的图像
def plot(X, Y, theta):
    import matplotlib.pyplot as plt
    ax = plt.subplot(111)  # 这是我改的
    ax.scatter(X, Y, s=30, c="red", marker="s")
    plt.xlabel("X")
    plt.ylabel("Y")
    x = arange(0, 21, 0.2)  # x的范围
    y = theta[0] + theta[1]*x
    ax.plot(x, y)
    plt.show()


plot(X1, Y, optimal)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

所拟合出的直线如下
在这里插入图片描述
全部代码如下，大家有兴趣的可以复制下来跑一下看一下结果：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2019/1/21 21:06
# @Author  : Arrow and Bullet
# @FileName: gradient_descent.py
# @Software: PyCharm
# @Blog    ：https://blog.csdn.net/qq_41800366

from numpy import *

# 数据集大小 即20个数据点
m = 20
# x的坐标以及对应的矩阵
X0 = ones((m, 1))  # 生成一个m行1列的向量，也就是x0，全是1
X1 = arange(1, m+1).reshape(m, 1)  # 生成一个m行1列的向量，也就是x1，从1到m
X = hstack((X0, X1))  # 按照列堆叠形成数组，其实就是样本数据
# 对应的y坐标
Y = array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(m, 1)
# 学习率
alpha = 0.01


# 定义代价函数
def cost_function(theta, X, Y):
    diff = dot(X, theta) - Y  # dot() 数组需要像矩阵那样相乘，就需要用到dot()
    return (1/(2*m)) * dot(diff.transpose(), diff)


# 定义代价函数对应的梯度函数
def gradient_function(theta, X, Y):
    diff = dot(X, theta) - Y
    return (1/m) * dot(X.transpose(), diff)


# 梯度下降迭代
def gradient_descent(X, Y, alpha):
    theta = array([1, 1]).reshape(2, 1)
    gradient = gradient_function(theta, X, Y)
    while not all(abs(gradient) <= 1e-5):
        theta = theta - alpha * gradient
        gradient = gradient_function(theta, X, Y)
    return theta


optimal = gradient_descent(X, Y, alpha)
print('optimal:', optimal)
print('cost function:', cost_function(optimal, X, Y)[0][0])


# 根据数据画出对应的图像
def plot(X, Y, theta):
    import matplotlib.pyplot as plt
    ax = plt.subplot(111)  # 这是我改的
    ax.scatter(X, Y, s=30, c="red", marker="s")
    plt.xlabel("X")
    plt.ylabel("Y")
    x = arange(0, 21, 0.2)  # x的范围
    y = theta[0] + theta[1]*x
    ax.plot(x, y)
    plt.show()


plot(X1, Y, optimal)
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66

5. 小结

至此，就基本介绍完了梯度下降法的基本思想和算法流程，并且用python实现了一个简单的梯度下降算法拟合直线的案例！
最后，我们回到文章开头所提出的场景假设:
这个下山的人实际上就代表了反向传播算法，下山的路径其实就代表着算法中一直在寻找的参数Θ，山上当前点的最陡峭的方向实际上就是代价函数在这一点的梯度方向，场景中观测最陡峭方向所用的工具就是微分 。在下一次观测之前的时间就是有我们算法中的学习率α所定义的。
可以看到场景假设和梯度下降算法很好的完成了对应！

本文部分内容来自一位前辈，非常感谢分享！谢谢！

posted @ 2021-02-05 17:59  常给自己加个油  阅读(202)  评论(0)  编辑  收藏  举报