ns-3中随机数机制
前言
ns-3是离散事件仿真平台,它由内核部分和常用模块两个部分组成。它的内核是用C++实现的。可以在src/core目录下查看,也可以在ns3的在线doxygen文档中查阅。
内核包含很多部分,实现了很多底层API供用户使用。因为仿真中经常需要模拟现实环境中的不确定行为,因而随机数机制是ns-3中非常重要的部分。了解随机数机制对仿真模拟真实随机情况非常重要,本文将详细讲解关于ns-3随机数的内容。
本文之后的部分将按照以下章节展开:
1.随机数生成器的背景
2.ns-3中的伪随机数生成器(PRNG,Pseudo Random Number Generator)
3.ns-3中常用的随机变量()
在第1点中将结合ns-3讨论常见的随机数生成器;在第2点中首先简单讲述ns-3中PRNG的特性,然后讲述ns-3中PNRG的常见使用方法;在第3点中介绍ns-3中常用的随机变量,包括满足均匀分布、正态分布、等差分布等的随机变量
一、背景:随机数生成器RNG
在了解ns-3中随机数机制之前,如果你之前对随机数生成器(RNG,Random Number Generator)理解的不是很清楚,非常有必要了解什么是随机数生成器。
计算机是按照事先确定的算法和程序进行确定的运算,都是确定性的计算。那么计算机到底是怎么得到随机数的?作为人类,我们大可提笔随便在纸上写一大串数字,也许就算是随机数了,但是计算机可没有这本事,它必须有一个科学稳定的随机数来源,才能得到随机数,这个来源,我们称为随机数生成器。
作为编程爱好者,应该会发现,每一门编程语言必然会有自己的随机数生成函数,常用的比如:C语言stdlib库中的rand()函数,java中Random类中的nextInt () 方法,Python中random模块的randint()方法等等。作为各种编程语言的“官方标配”,这小小的随机函数作用那也是大大的,不光而这看似简单的东西背后学问还真不少。
常见的计算机随机数生成器有三种:
参考文章 : 解密随机数生成器
一是使用物理方法,称为真随机数生成器(True Random Number Generator),生成的算是真正意义上的随机数,无法预测且无周期性;
与真随机数对应的是伪随机数生成器(Pseudo Random Number Generator),它是由算法计算得来的,但这种方法生成的随机数是可预测、有周期的,并不能算真的随机数,因此得名伪随机数;
还有第三种方法,叫随机数表法,就是用真随机数生成器事先生成好大量随机数,存到数据库中,使用时再从库中调用。记得高中数学书第三册后附有一个叫随机数表的东西,使用时直接查阅就行,这种方法简单,但缺点是内存占用大,因此不常采用。
在编程当中常常使用的就是伪随机数生成器。
伪随机数算法中重要术语:
PRNG中常常需要给定一个种子,映射出一个不确定的随机数。需要划重点的是:不同的种子映射的数值可以认为是没有规律的,可以认为是随机的。在这样的映射条件下,才有我们所说的随机数生成器,否则如果是确定的一一映射,完全无法体现随机这样一个概念。
每一个伪随机数生成器(PRNG)都会提供一个相当长的随机数序列,这个序列的长度称为循环周期或者循环长度,RNG在完成一次循环后将自动进行下一次重复。这个序列可以被分隔为几个相互独立的数据流。一个RNG的随机数据流是这个RNG序列的连续子集。例如,一个RNG队列长度为N,同时RNG提供2个数据流,第一个数据流使用序列的前半部分,第二个数据流使用序列的后半部分,这两个数据流是相互独立的。同样,每一个数据流还可以被分为更小的子流。
一个RNG最希望做到的就是提供一个非常长的循环序列,并有效的分配给每一个数据流。
伪随机数生成器有很多种算法,包括同余法、梅森旋转算法等多种多样的方法,我们此处重点介绍一下prerre L’Ecuyer提出的MRG32k3a生成器。它提供1.8*1 019相互独立的数据流,每个数据流又包含2.3*1 015个子数据流,并且每一个子数据流用甘油7.6*1 022的长度,因此整个生成器的循环周期为3.1*1 057。正因为RNG拥有这么长的序列,才保证了RNG产生的随机数具有很高的可信度。
MRG32k3生成器需要一个随机数种子,
敲黑板!敲黑板!敲黑板!
1.计算机一般都是确定性的计算和运行,只有借助随机数生成器才可以产生随机数
2.三种随机数生成器中,伪随机数生成器PRNG在编程中使用最频繁
3.伪随机数中,由种子映射到随机数时候可以认为映射是没有规律、是随机的
4.伪随机数生成器的循环周期足够长能够保证RNG的随机数具有更高的可信度
二、详解:ns-3中PRNG的使用
在ns-3中,仿真程序通常使用固定的种子,也就是产生固定的随机数,也就是固定的数值,所以仿真也就不存在不确定性,也即确定性仿真。
如果需要模拟不确定的情况,则需要改变PRNG的种子或者运行标识。
ns-3的随机数通过调用类ns3::RandomVariableStream来提供(在3.14版本及之前有ns3::Random Variable提供)。ns3::RandomVariableStream是对底层的随机数生成器进行封装之后向用户提供的使用接口。
PRNG的种子和运行标识分别存储在类GlobalValue的g_rngSeed和g_rngRun中,改变PRNG的种子或者运行标识通过ns3::RngSeedManager::SetSeed()和ns3::RngSeedmanager::SetRun()进行,下面对两种改变方式分别做介绍。
2.1 通过ns3::RngSeedManager::SetSeed()改变种子实现随机性
#include "ns3/simulator.h"
#include "ns3/nstime.h"
#include "ns3/command-line.h"
#include "ns3/rng-seed-manager.h"
#include "ns3/random-variable-stream.h"
#include <iostream>
using namespace ns3;
int main(int argc, char *argv[])
{
CommandLine cmd;
cmd.Parse(argc,argv);
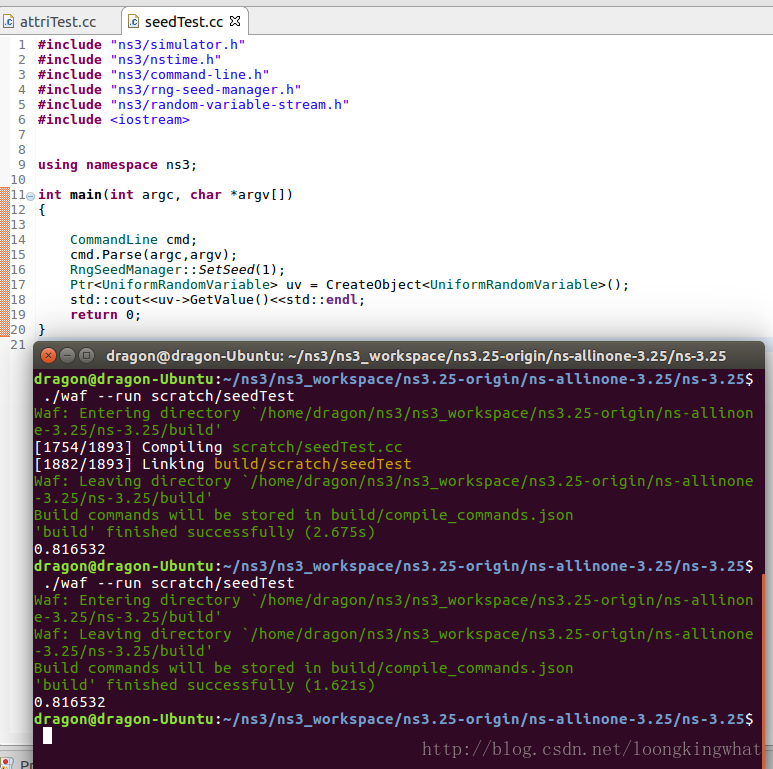
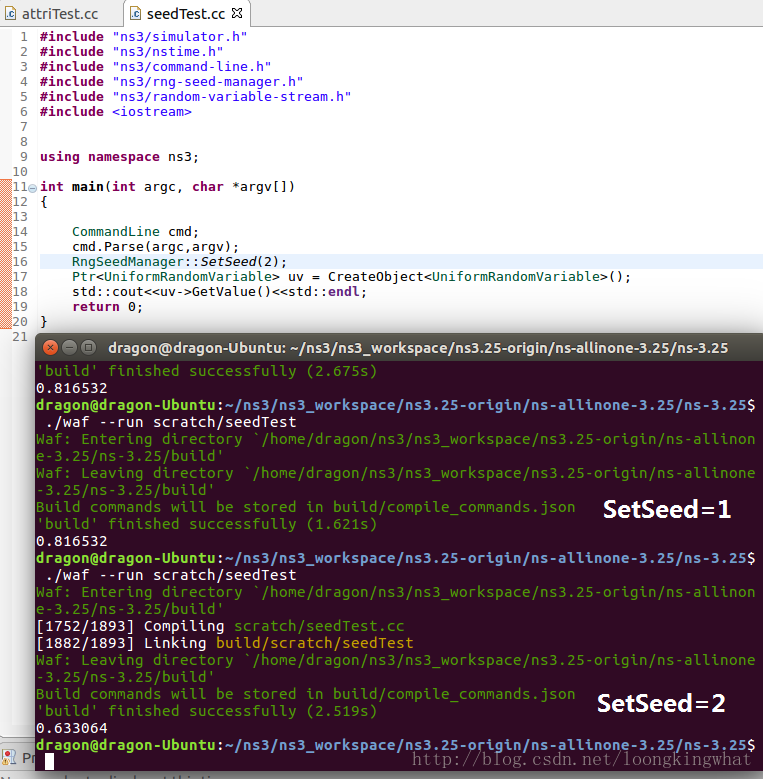
RngSeedManager::SetSeed(1);
Ptr<UniformRandomVariable> uv = CreateObject<UniformRandomVariable>();
std::cout<<uv->GetValue()<<std::endl;
return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
上述代码中,首先通过RngSeedManager::SetSeed(1)设置种子为1,然后创建了一个类型为UniformRandomVariable的智能指针Ptr,其中UniformRandomVariable是ns3::RandomVariableStream的子类,所以通过uv调用GetValue()函数获得对应的值。
运行结果如下:
对于这个例子,在不改变SetSeed()函数参数的情况下连续运行两次,得到的随机数是一样的,如上图中所示,结果都是0.816532。将SetSeed()函数的参数修改为2,在运行一下,运行结果如下图,发现改变种子之后,得到的随机数结果是不一样的,seed=2的时候的结果变成0.633064。
2.2 通过ns3::RngSeedmanager::SetRun()改变运行标识实现随机性
在不改变种子的条件下,也可以通过改变 运行标识 来实现随机性,改变运行运行标识的方法也有4种:
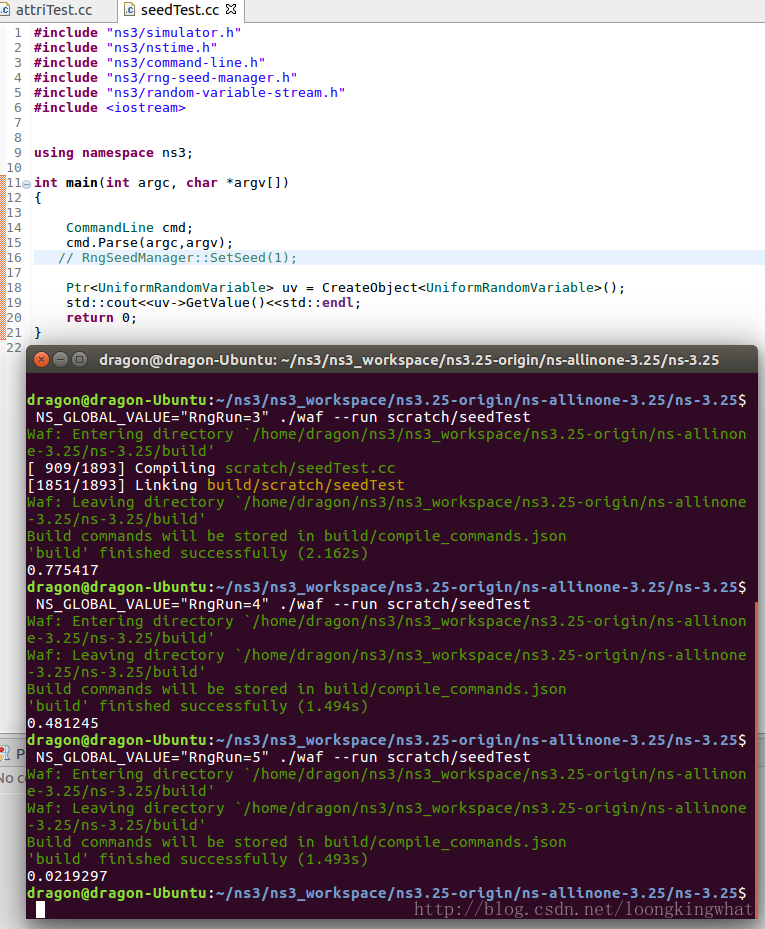
①通过函数RngSeedManager::SetRun(4)改变运行标识
以下的实验中,分别使用RngSeedManager::SetRun(3)和RngSeedManager::SetRun(4)运行得到结果。
②通过修改环境变量NS_GLOBAL_VALUE的值来修改运行标识
这种方法不需要对代码做修改,只需要在运行时候,在命令窗口进行设置。
NS_GLOBAL_VALUE="RngRun=3"./waf --run program-name- 1
③通过命令行传递参数来修改运行标识
这种方法也不需要对代码做修改,只需要在运行时候,在命令窗口进行设置。
./waf --run "program-name --RngRun=3"- 1
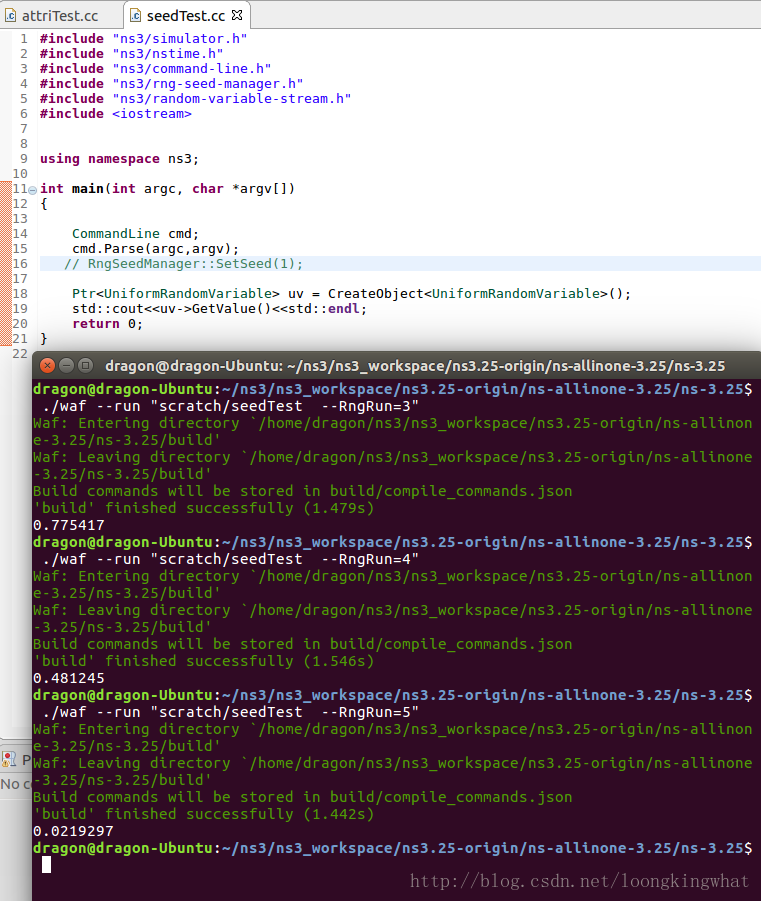
④这种方式不使用waf,而是直接使用build
./build/optimized/scratch/program-name --RngRun=3- 1
这种方法不太适用,此处不做演示。
**针对上述4种方式,第1种与改变方式的方式基本上是一致的,只需要把代码行RngSeedManager::SetSeed()用代码行RngSeedManager::SetRun()替换就可以,每次进行独立运行时改变参数就行。第二种方式比较繁琐,每次都要修改环境变量,所以建议还是使用第三种方法。
**需要注意的是:提倡使用改变运行标识的方法实现随机性。因为在改变种子的情况下进行重复试验,ns-3无法保证每个种子对应的RNG序列不会重复。而修改运行标识是使用RNG序列的不同的子序列,同一个RNG序列的子序列是不会重复的。
三、详解:ns-3中的随机变量类型
ns-3中一共有5种常用的随机变量,这5种都是
1.满足均匀分布的随机数
2.满足正态分布的随机数
3.满足指数分布的随机数
4.满足等差序列的随机数
5.返回一个固定的数值
以上5种分别对应了RandomVariableStream类的5个子类,下面一一进行解释。
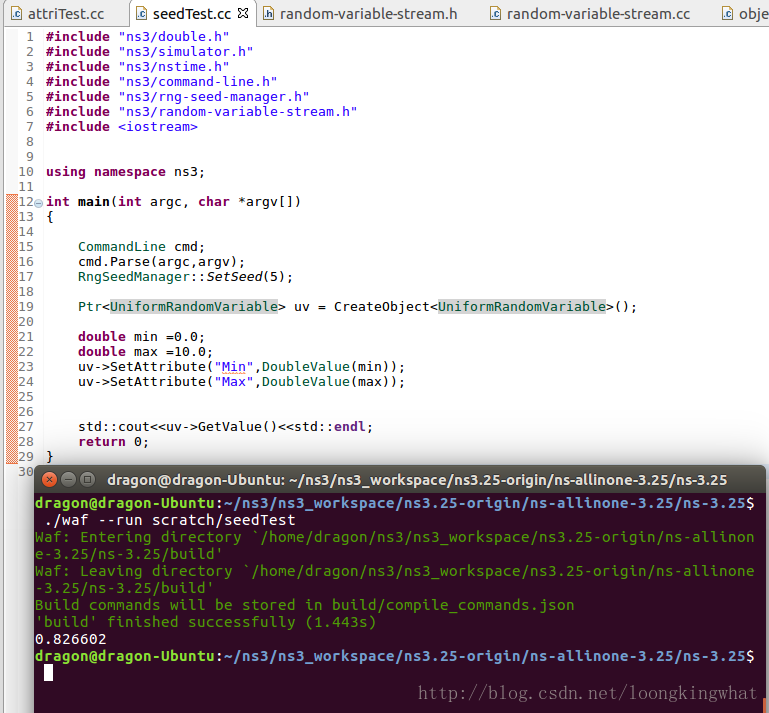
1.UniformRandomVariable:给定最大值和最小值,按均匀分布的方式返回一个随机数
UniformRandomVariable是从RandomVariableStream继承的派生类,也是最基础和最常用的类。它有两个属性:
| 属性名称 | 含义 | 类型 |
|---|---|---|
| Max | 均匀分布区间的上界 | ns3::DoubleValue |
| Min | 均匀分布区间的下界 | ns3::DoubleValue |
以下是一个实例:
2.NormalRandomVariable:根据正态分布返回随机数
需要设置的属性值包括:
| 属性名称 | 含义 | 类型 | 初始值 |
|---|---|---|---|
| Mean | 返回值的均值 | ns3::DoubleValue | 0 |
| Valance | 返回值的方差 | ns3::DoubleValue | 1 |
| Bound | 返回值的上界 | ns3::DoubleValue | 1*10^307 |
3.ExponentialRandomVariable:根据指数概率分布返回随机数
需要设置的属性值包括:
| 属性名称 | 含义 | 类型 | 初始值 |
|---|---|---|---|
| Mean | 返回值的均值 | ns3::DoubleValue | 1 |
| Bound | 返回值的上界 | ns3::DoubleValue | 0 |
4.SequentialRandomVariable:返回一串等差序列
如果超过了给定的最大上限,则重新从给定的最小值开始循环。序列随机变量的常用属性如下:
| 属性名称 | 含义 | 类型 | 初始值 |
|---|---|---|---|
| Min | 序列的最小值 | ns3::DoubleValue | 0 |
| Max | 序列最大值的上限 | ns3::DoubleValue | 0 |
| Increment | 序列的差值 | ns3::PointerValue | 1 |
| consecutive | 序列中每个数重复的次数 | ns3::StringeValue | 1 |
5.ConstantRandomVariable:返回一个固定的数
其默认值是0,使用方法和均匀分布的例子一样。
RngSeedManager::SetSeed(3);
double dValue=10.0 //把默认初始值改为10
Ptr<ConstantRandomVariable> uv = CreateObject<ConstantRandomVariable>();
uv->SetAttribute("Constant",DoubleValue(dValue));