[再谈/浅谈]积性函数求和
为啥是再谈呢,因为我假装以前发过积性函数求和的blog,假装没有咕咕咕
Min_25筛
设 \(P\) 为素数集合,\(p_i\) 为素数集合中的第 \(i\) 个数,\(m_i\) 为一个数 \(i\) 的最小质因数
首先我们要求:
\[\sum\limits_{i=1}^n[i\in P]i^k
\]
设:
\[g_{n,i}=\sum\limits_{j=1}^n[j\in P\or m_j>p_i]j^k
\]
并且我们记前缀和 \(s_i\):
\[s_i=\sum\limits_{j=1}^ip_j^k
\]
容易发现 \(g_{n,i}\) 就是 \([1,n]\) 中进行 \(i\) 轮埃氏筛后未被筛掉的数的 \(k\) 次方之和
显然,如果设 \(cnt\) 为 \([1,\sqrt n]\) 内的质数个数,那么有:
\[\sum\limits_{i=1}^n[i\in P]i^k=g_{n,cnt}
\]
现在我们要求的即为 \(g_{n,i}\) 的递推式,假设现在我们已经求出了 \(g_{n,i-1}\)
考虑这次被筛掉的数即为最小质因子等于 \(p_i\) 的数,其一定可以表示为 \(kp_i\)
于是我们提取 \(p_i\),转而枚举 \(k\)
由 \(g\) 函数的定义,我们还要加上之前的一些质数,因为它们不可能被筛掉
于是我们就可以很轻易的得出:
\[g_{n,i}=\begin{cases}
g_{n,i-1}&&&&&p_i>\sqrt n
\\
g_{n,i-1}-p_i^kg_{\lfloor\frac{n}{p_i}\rfloor,i-1}+p_i^ks_{i-1}&&&&&p_i\le\sqrt n
\end{cases}
\]
现在我们来考虑 \(f_i\),\(f\) 是一个积性函数,其中 \(\forall p_i\in P\),\(f_{p_i}\) 可以表示为多项式的形式,并且 \(f_{p_i^k}\) 可以快速计算
现在我们要求:
\[\sum\limits_{i=1}^nf_i
\]
像上文一样,设:
\[s_{n,i}=\sum\limits_{j=1}^n[m_j> p_i]f_j
\]
于是:
\[\sum\limits_{i=1}^nf_i=s_{n,0}
\]
现在我们要计算 \(s_{n,i}\),我们将质数与合数对 \(s_{n,i}\) 的贡献分别进行计算,最后相加即可
首先根据上文,快速计算质数的贡献已经讨论完毕,即:
\[\sum\limits_{j=1}^n[j\in P]f_j-\sum\limits_{j=1}^{i-1}f_{p_j}
\]
现在我们考虑合数的贡献,而这只需要枚举最小质因子及其出现次数即可,即:
\[\sum\limits_{j=i}^{p_j^2\le n}\sum\limits_{k=1}^{p_j^{k}\le n}\left( f_{p_j^k}(s_{\lfloor n/p_j^k\rfloor,j}+[k>1])\right)
\]
综上,我们可以得出 \(s_{n,i}\) 的计算方式
\[s_{n,i}=\begin{cases}
0&&p_i>n
\\
\sum\limits_{j=1}^n[j\in P]f_j-\sum\limits_{j=1}^{i-1}f_{p_j}+\sum\limits_{j=i}^{p_j^2\le n}\sum\limits_{k=1}^{p_j^{k}\le n}\left( f_{p_j^k}(s_{\lfloor n/p_j^k\rfloor,j}+[k>1])\right)&&p_i\le n
\end{cases}
\]
LG. 5493 质数前缀统计
洲阁筛与Min_25筛前置,但是可有可无,直接做也可以
首先对于自然数幂和,我们已经非常熟悉:
\[f(n)=\sum\limits_{i=1}^{k+2}(-1)^{k-i+2}\dfrac{y_i(n-1)^{\underline{k+2}}}{(i-1)!(k-i+2)!(n-i)}
\]
这个东西可以 \(O(k)\) 计算,对于 \(n\) 较小的情况,计算相对麻烦一点,我们需要上下同除 \(n-i\)
然后我们来看本题,求:
\[\sum\limits_{i=1}^{\lfloor\sqrt n\rfloor}i^2S\left(\left\lfloor\dfrac n i\right\rfloor\right)
\]
实际上,我们需要求的仅仅是 \(S\) 函数的值
根据上文,我们设一个函数 \(f\),满足 \(f_{n,i}\) 为 \([1,n]\) 中 \(m_j>p_i\) 的数的 \(k\) 次方和,\(m_j\) 的含义与上文的定义相同
换句话来说,\(f_{n,i}\) 就是 \([1,n]\) 中用埃氏筛筛 \(i\) 轮之后剩下的数的 \(k\) 次方和
而这,我们已于上文讨论过
于是我们维护一个 \(s\) 数组,\(s_i\) 维护 \(S(\lfloor\frac n i\rfloor)\) 的值,再维护一个 \(h\) 数组,\(h_i\) 维护 \(S(i)\) 的值
对于 \(\lfloor\frac{n}{p_i}\rfloor\),如果其大于 \(\sqrt n\),那么我们用 \(s\) 去更新它,否则,我们用 \(h\) 更新它
直接做就可以了
杜教筛
这东西比较基础,就放在min_25筛之后了,算是一个总结
狄利克雷卷积
给定函数 \(f,g\),定义两个函数的卷积乘法 \(*\) 为:
\[(f*g)(x)=\sum\limits_{d|n}f(d)g\left(\dfrac n d\right)
\]
那么在狄利克雷卷积意义下,一个函数的逆为:
\[f^{-1}(n)=\dfrac 1 {f(1)}\left(\epsilon(n)-\sum\limits_{d|n\and d\ne 1}f(d)f^{-1}\left(\dfrac n d\right)\right)
\]
证明,利用数学归纳法:
\[\begin{align*}
(f*f^{-1})(x)&=\sum\limits_{d|n}f(d)f^{-1}\left(\dfrac n d\right)
\\
&=f(1)f^{-1}(n)+\sum\limits_{d|n\and d\ne 1}f(d)f^{-1}\left(\dfrac n d\right)
\\
&=\epsilon(n)
\end{align*}
\]
杜教筛
给定函数 \(f\),我们现在要求其前缀和,即:
\[s(n)=\sum\limits_{i=1}^nf(i)
\]
朴素的算法是 \(O(n)\) 的,但是现在假设我们有一个积性函数 \(g\),我们去构造它的狄利克雷卷积:
\[\begin{align*}
\sum\limits_{i=1}^n(f*g)(i)&=\sum\limits_{i=1}^n\sum\limits_{d|i}g(d)f\left(\dfrac i d\right)
\\
&=\sum\limits_{d=1}^ng(d)\sum\limits_{i=1}^{\lfloor\frac n d\rfloor}f(i)
\\
&=\sum\limits_{d=1}^ng(d)S\left(\left\lfloor\dfrac n d\right\rfloor\right)
\\
&=g(1)S(n)+\sum\limits_{d=2}^ng(d)S\left(\left\lfloor\dfrac n d\right\rfloor\right)
\end{align*}
\]
因此,我们可以得到 \(S(n)\) 关于 \(S(\lfloor\frac n d\rfloor)\) 的一个递推式:
\[g(1)S(n)=\sum\limits_{i=1}^n(f*g)(i)-\sum\limits_{d=2}^ng(d)S\left(\left\lfloor\dfrac n d\right\rfloor\right)
\]
复杂度使用积分近似,即:
\[\begin{align*}
O\left(\sum\limits_{i=1}^\sqrt n\sqrt{\left\lfloor\dfrac n i\right\rfloor}\right)&=O\left(\int_{1}^\sqrt n\sqrt{\dfrac n x}\text dx\right)
\\
&=O(n^{\frac 3 4})
\end{align*}
\]
但是我们可以对较小的 \(n\) 进行预处理,这样一来,复杂度为
\[O\left(n^k+\sum\limits_{i=1}^{n^{1-k}}\sqrt{\left\lfloor\dfrac n i\right\rfloor}\right)=O(n^k+n^{1-\frac 1 2 k})
\]
取 \(k=\frac 2 3\) 即可,复杂度 \(O(n^\frac 2 3)\),个人认为多测用 map,单测直接记下取整的分母比较好
定义点乘 \((f·g)(x)=f(x)g(x)\)
如果 \(f\) 是完全积性函数,\(g,h\) 为数论函数,那么 \(((f·g)*(f·h))(x)=(f·(g*h))(x)\)
证明的话也比较简单:
\[((f·g)*(f·h))(x)=\sum\limits_{d|n}f(d)g(d)f\left(\dfrac n d\right)h\left(\dfrac n d\right)=f(n)\sum\limits_{d|n}g(d)h\left(\dfrac n d\right)=(f·(g*h))(x)
\]
如果设 \(f,g\) 为两个数论函数,\(h\) 为一个完全积性函数,且满足 \(h(1)=1\),那么此时我们有:
\[f(n)=\sum\limits_{d=1}^nh(d)g\left(\left\lfloor\dfrac n d\right\rfloor\right)\Leftrightarrow g(n)=\sum\limits_{d=1}^n\mu(d)h(d)f\left(\left\lfloor\dfrac n d\right\rfloor\right)
\]
证明也不难:
\[\begin{align*}
\sum\limits_{d=1}^nh(d)g\left(\left\lfloor\dfrac n d\right\rfloor\right)&=\sum\limits_{d=1}^n
h(d)\sum\limits_{k=1}^{\lfloor\frac n d\rfloor}\mu(k)h(k)f\left(\left\lfloor\dfrac n{kd}\right\rfloor\right)
\\
&=\sum\limits_{i=1}^n\sum\limits_{k|i}h(i)\mu(k)f\left(\left\lfloor\dfrac n i\right\rfloor\right)
\\
&=\sum\limits_{i=1}^nf\left(\left\lfloor\dfrac n i\right\rfloor\right)h(i)\epsilon(i)
\\
&=f(n)
\end{align*}
\]
LG. 3768 简单的数学题
首先我们有一个广为人知的结论:
\[\sum\limits_{d|n}\varphi(d)=n
\]
因此我们可以用 \(\gcd(x,y)\) 替换 \(n\) 获得另一个关于 \(\gcd\) 的等式
\[\begin{align*}
\sum\limits_{i=1}^{n}\sum\limits_{j=1}^nij\gcd(i,j)&=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^nij\sum\limits_{d|i\and d|j}\varphi(d)
\\&
=\sum\limits_{d=1}^n\varphi(d)\sum\limits_{i=1}^{\lfloor\frac n d\rfloor}id\sum\limits_{j=1}^{\lfloor\frac n d\rfloor}jd
\\
&=\sum\limits_{d=1}^nd^2\varphi(d)S\left(\left\lfloor\dfrac n d\right\rfloor\right)^2
\end{align*}
\]
我们需要对 \(S\) 进行分块,因此我们就需要快速求出 \(d^2\varphi(d)\) 的前缀和
我们发现 \(d^2=\text{id}^2\),是一个完全积性函数,因此,根据之前的引理,我们只需要构造一个函数 \(h\),使得 \(\varphi *h\) 可以快速计算即可
显然 \(h\) 应该取常值函数,现在即构造 \(g=\text{id}^2*1=\text{id}^2=n^2\),我们即可得到 \(S(n)\):
\[S(n)=\sum\limits_{i=1}^ni^3-\sum\limits_{i=1}^Ni^2S\left(\left\lfloor\dfrac n i\right\rfloor\right)
\]
嗯,然后就做完了
贝尔级数
对于积性函数 \(f(n)\),定义其在质数 \(p\) 意义下的贝尔级数为
\[F_p(x)=\sum\limits_{i=0}^\infty f(p^i)x^i
\]
此时,一些常见的数论函数的贝尔级数为(默认除数函数 \(\sigma\) 为 \(\sigma_0\)):
所以表格为什么没有办法正常渲染啊qwq
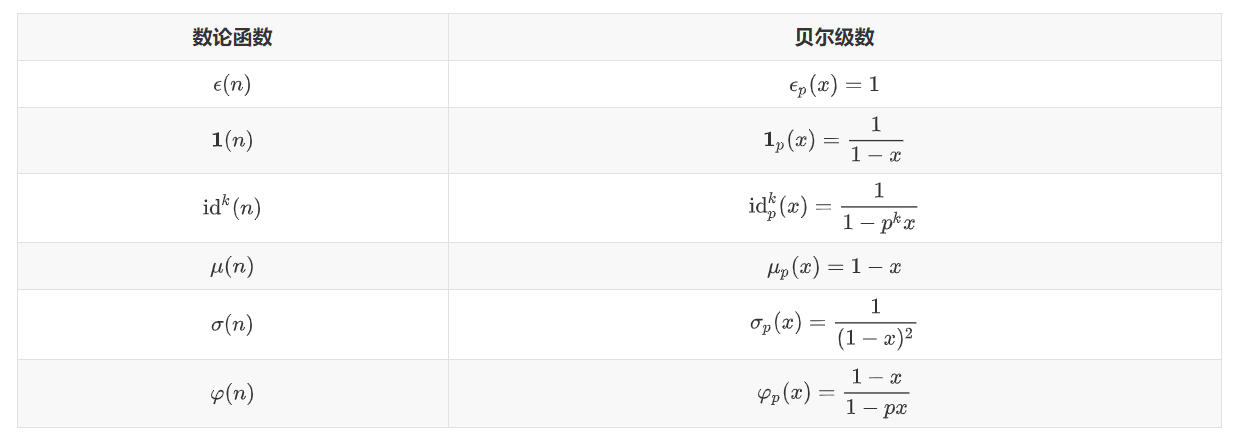
贝尔级数将狄利克雷卷积变成了一般卷积,即:
\[(f*g)_p(x)=f_p(x)g_p(x)
\]
from rqy's blog
给定一个积性函数 \(f\),满足 \(f(p^k)=p^k+[k>0](-1)^k\),求 \(f\) 的前缀和
令左右两边同时加上 \(1\),现在 \(f(p^k)+1=\dfrac{1}{1-px}+\dfrac1{1+x}\)
因此如果我们取 \(g_p(x)=(1-px)(1+x)\),那么 \(h_p(x)=1+px^2\)
观察 \(h(n)\),发现当且仅当 \(h=p_1^2\cdots p_k^2\) 时,\(h(n)=\sqrt n\)
因此
\[\sum\limits_{i=1}^nh(i)=\sum\limits_{i=1}^{\lfloor\sqrt n\rfloor}i\mu^2(i)
\]
现在我们来观察 \(g_p(x)\),这也是很好计算的,事实上,我们展开就能发现 \(g=(\text{id}·\mu)*\mu^2\)
而这也是非常好计算的,通过上文的引理,我们只需要令 \(g=\text{id}\)
此时
\[S(n)=\sum\limits_{i=1}^n\mu^2(i)-\sum\limits_{i=2}^niS\left(\left\lfloor\dfrac n i\right\rfloor\right)
\]
现在我们发现两个前缀和中都是含有 \(\mu^2(i)\) 的,因此我们最后的任务变成了求
\[S(n)=\sum\limits_{i=1}^n\mu^2(i)
\]
首先我们知道 \(\mu^2(n)\) 不为 \(0\) 的条件就是 \(n\) 不含平方因子,因此如果我们设 \(m_i\) 为其最大的平方因子,那么可以得到一个等式:
\[\mu^2(i)=[m_i=1]
\]
所以我们用 \(\mu*\text{id}\) 来判定即可
又因为 \(d^2|i \Leftrightarrow d|m_i\),所以我们可以得到一个等式:
\[\mu^2(i)=\sum\limits_{d^2|i}\mu(d)
\]
因此,我们可以在 \(O(\sqrt n)\) 的时间内计算其前缀和:
\[\sum\limits_{i=1}^n\mu^2(i)=\sum\limits_{i=1}^n\sum\limits_{d^2|i}\mu(d)=\sum\limits_{d=1}^\sqrt n\mu(d)\left\lfloor\dfrac n{d^2}\right\rfloor
\]
Powerful Number
定义
如果一个数 \(n=p_1^{a_1}p_2^{a_2}\cdots p_k^{a_k}\),且满足 \(a_1,a_2,\cdots,a_k\ge 2\),那么数 \(n\) 称作 \(\texttt{powerful number}\)
区间 \([1,n]\) 中,\(\texttt{powerful number}\) 只有 \(O(\sqrt n)\) 个
显然 \(\texttt{powerful number}\) 一定可以被表示成 \(a^2b^3\) 的形式,其中 \(a,b\) 不一定是质数
因此,我们利用积分进行近似,即可得出 \(\texttt{powerful number}\) 的个数:
\[\begin{align*}
O\left(\sum\limits_{i=1}^\sqrt n\left(\dfrac n{i^2}\right)^{\frac1 3}\right)&=O\left(\int_{1}^\sqrt n\left(\dfrac n{i^2}\right)^{\frac1 3}\text di\right)
\\
&=O\left(n^{\frac 1 3}\int_{1}^\sqrt ni^{-\frac2 3}\text di\right)
\\
&=O\left(\sqrt n\right)
\end{align*}
\]
我们以Min_25筛的模板题为例来看看 \(\texttt{powerful number}\) 是如何应用的
本题对于一个质数 \(p\),\(f(p)=p(p-1)\),那么我们现在设一个数论函数 \(g(p)=p\varphi(p)\)
显然 \(f=g\),现在我们再设一个函数 \(h\),满足 \(h(1)=1\) 且在狄利克雷卷积意义下,\(f=g*h\)
根据上文提到的,我们知道 \(h\) 是唯一的一个积性函数
根据 \(p\) 是一个质数,此时我们有:
\[f(p)=g(1)h(p)+g(p)h(1)
\]
根据此式,显然 \(h(p)=0\)
因此,当且仅当 \(n\) 是一个 \(\texttt{powerful number}\) 时,\(h(n)\) 才有可能不为零
现在我们考虑如何计算答案:
\[\begin{align*}
\sum\limits_{i=1}^nf(i)&=\sum\limits_{i=1}^n\sum\limits_{d|i}g(d)h\left(\dfrac i d\right)
\\
&=\sum\limits_{d=1}^ng(d)\sum\limits_{k=1}^{\lfloor\frac n d\rfloor}h(k)
\end{align*}
\]
现在我们要计算 \(h(p^k)\) 的值,根据条件,我们有:
\[f(p^k)=\sum\limits_{i=0}^kg(p^i)h(p^{k-i})
\]
将我们已知的东西带进去:
\[p^k(p^k-1)=\sum\limits_{i=0}^k(p-1)p^{2i-1}h(p^{k-i})
\]
因此:
\[h(p^k)=(k-1)(p^{k+1}-p^k)
\]
利用杜教筛筛出 \(h\) 的值,暴力枚举质因子搜索出 \(\texttt{powerful number}\) 然后加进答案即可



 浙公网安备 33010602011771号
浙公网安备 33010602011771号