有源汇上下界最大流

关于普通网络流，想必各位读者已经非常熟悉，故在此不对网络最大流做过多介绍

在阅读本文前，请确保您已经学会Dinic和ISAP算法并会简单的应用

无源汇上下界可行流

有源汇上下界最大流，顾名思义即为一条边有流量上限，也有流量下限，同时给出了源点与汇点

但是一张图不可能必定有可行的流，举个例子：

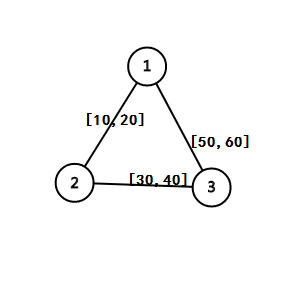
在这张图中，很显然的没有可行流

故我们首先考虑在无源汇的时候，一张图有没有可行的流

很自然的，大家应该都会有一个想法，即流量上限减去流量下限

同样很自然的，大家都能直接HACK掉这个想法

你可能会问了，这不跟没说一样么？

看起来没用，但是我们要在这个想法上做文章

我们将所有连入点 \(p\) 的边的流量下界统计起来，作为其入流

然后再将连出点 \(p\) 的边的流量下界统计起来，作为其出流

我们知道一个图上只有源点与汇点不满足流量守恒，所以只要设法把点 \(p\) 的入流和出流差消掉就可以了

都说到这里了，是不是很显然的就能发现将多出来的流推给源点和汇点就可以了？

所以我们的思路也很明确了：

虚拟源点与汇点
在原图上连边，边的流量设为流量上界减去流量下界
统计每个点的入流与出流，如果入流大于出流，那么从源点向这个点连边，反之从这个点向汇点连边，流量即为入流与出流的差
从虚拟源点向虚拟汇点跑最大流，如果流能跑满，即从源点出发没有一条有剩余流量的边，说明有可行流，反之则没有

还是举个例子：

转化之后就是

显然这张图的流可以跑满，故存在可行流

最后，一定要注意边的起点与终点！！

LOJ #115.无源汇有上下界可行流

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 1000001
#define M 5001
#define INF 400000000
#define Kafuu return
#define Chino 0
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define R register
#define C const
using namespace std;
int dep[N],depn[N],n,m,lo,up,head[N],cur[N],num=1,s,t,in[N],out[N],ans,fr,to,sum;
struct Edge{
	int fl,na,np,lo;
}e[N];
fx(void,add)(int f,int t,int fl,int lo=-1){
	e[++num].na=head[f];
	e[num].np=t,e[num].fl=fl,e[num].lo=lo;
	head[f]=num;
}
fx(int,gi)(){
	R char c=getchar();R int s=0,f=1;
	while(c>'9'||c<'0'){
		if(c=='-') f=-f;
		c=getchar();
	}
	while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
	return s*f;
}
queue<int>q;
fx(void,layer)(){
	set(dep,-1,int,N);
	dep[t]=0;depn[0]=1;int f;q.push(t);
	while(!q.empty()){
		f=q.front();q.pop();
		for(int i=head[f];i;i=e[i].na){
			if(dep[e[i].np]==-1){
				dep[e[i].np]=dep[f]+1;
				depn[dep[e[i].np]]+=1;
				q.push(e[i].np);
			}
		}
	}
}
fx(int,ISAP)(int now,int rf){
	if(now==t) return rf;
	int af=0,tf=0;
	for(int i=cur[now];i;i=e[i].na){
		cur[now]=i;
		if(!e[i].fl) continue;
		if(dep[e[i].np]==dep[now]-1){
			af=ISAP(e[i].np,min(e[i].fl,rf));
			if(af){
				e[i].fl-=af;e[i^1].fl+=af;
				tf+=af;rf-=af;
			}
			if(!rf) return tf;
		}
	}
	depn[dep[now]]-=1;
	if(!depn[dep[now]]) dep[s]=t+1;
	depn[++dep[now]]++;
	return tf;
}
signed main(){
	n=gi(),m=gi();s=n+1,t=n+2;
	for(int i=1;i<=m;i++){
		fr=gi(),to=gi(),lo=gi(),up=gi();
		in[to]+=lo;out[fr]+=lo;
		add(fr,to,up-lo,lo);add(to,fr,0);
	}
	for(int i=1;i<=n;i++){
		if(in[i]==out[i]) continue;
		else if(in[i]>out[i]){
			add(s,i,in[i]-out[i]);
			add(i,s,0);
			sum+=in[i]-out[i];
		} else {
			add(i,t,out[i]-in[i]);
			add(t,i,0);
		}
	}
	layer();
	while(dep[s]<t+1){
		cpy(head,cur,int,N);
		ans+=ISAP(s,INF);
	}
	if(ans!=sum){
		printf("NO\n");
		Kafuu Chino;
	}
	printf("YES\n");
	for(int i=2;i<=num;i+=2) if(e[i].lo!=-1) printf("%d\n",e[i^1].fl+e[i].lo);
}

有源汇上下界最大流

我们现在不单单要找可行流了，现在还要使流量最大，即找出最大流

先不着急思考，我们先来看看这个问题和上文的问题区别在哪里

首先，有了源点与汇点

其次，要找最大流

上文说到源点和汇点不满足流量守恒，但是如果我们稍微想想就能发现：从源点流出的流与到汇点汇入的流是相等的！

我们发现，现在如果将汇点与源点之间连一条容量为 \(\infty\) 的边，那么这个问题不就已经转化为上面我们讨论过的问题了么

现在考虑如何能使流最大

首先，与虚拟源点相连的边的剩余流量都已经空了，所以我们要想再找出一条增广路，从虚拟的源点与汇点上做文章是不行了

诶，原来的图是不是还能跑出来增广路啊！

我们将连接原来的汇点与源点的那条容量为 \(\infty\) 的边去掉，然后在原来的图上跑增广路，如果能跑出流量，可以验证，这流量一定是合法的，我们只需要加上即可

综上，我们的思路是：

连接源点与汇点，按照无源汇上下界可行流的操作来一遍，设此时的可行流为 \(flow_1\)
断开连接的边，在原图上跑增广路，此时跑出的流量为 \(flow_2\)
得到答案：\(flow_1+flow_2\)

LOJ #116.有源汇有上下界最大流

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 1000001
#define M 5001
#define INF 400000000
#define Kafuu return
#define Chino 0
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define R register
#define C const
using namespace std;
int dep[N],depn[N],n,m,lo,up,head[N],cur[N],num=1,vs,vt,s,t,in[N],out[N],ans,fr,to,sum,pl;
struct Edge{
	int fl,na,np,lo;
}e[N];
fx(void,add)(int f,int t,int fl,int lo=-1){
	e[++num].na=head[f];
	e[num].np=t,e[num].fl=fl,e[num].lo=lo;
	head[f]=num;
}
fx(int,gi)(){
	R char c=getchar();R int s=0,f=1;
	while(c>'9'||c<'0'){
		if(c=='-') f=-f;
		c=getchar();
	}
	while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
	return s*f;
}
queue<int>q;
fx(void,layer)(int t){
	set(dep,-1,int,N);
	dep[t]=0;depn[0]=1;int f;q.push(t);
	while(!q.empty()){
		f=q.front();q.pop();
		for(int i=head[f];i;i=e[i].na){
			if(dep[e[i].np]==-1){
				dep[e[i].np]=dep[f]+1;
				depn[dep[e[i].np]]+=1;
				q.push(e[i].np);
			}
		}
	}
}
fx(int,ISAP)(int now,int rf,int s,int t){
	if(now==t) return rf;
	int af=0,tf=0;
	for(int i=cur[now];i;i=e[i].na){
		cur[now]=i;
		if(!e[i].fl) continue;
		if(dep[e[i].np]==dep[now]-1){
			af=ISAP(e[i].np,min(e[i].fl,rf),s,t);
			if(af){
				e[i].fl-=af;e[i^1].fl+=af;
				tf+=af;rf-=af;
			}
			if(!rf) return tf;
		}
	}
	depn[dep[now]]-=1;
	if(!depn[dep[now]]) dep[s]=t+1;
	depn[++dep[now]]++;
	return tf;
}
signed main(){
	n=gi(),m=gi();s=gi(),t=gi();
	vs=n+1,vt=n+2;
	for(int i=1;i<=m+1;i++){
		if(i==m+1) fr=t,to=s,lo=0,up=INF,pl=num+1;
		else fr=gi(),to=gi(),lo=gi(),up=gi();
		in[to]+=lo;out[fr]+=lo;
		add(fr,to,up-lo,lo);add(to,fr,0);
	}
	for(int i=1;i<=n;i++){
		if(in[i]==out[i]) continue;
		else if(in[i]>out[i]){
			add(vs,i,in[i]-out[i]);
			add(i,vs,0);
			sum+=in[i]-out[i];
		} else {
			add(i,vt,out[i]-in[i]);
			add(vt,i,0);
		}
	}
	layer(vt);
	while(dep[vs]<vt+1){
		cpy(head,cur,int,N);
		ans+=ISAP(vs,INF,vs,vt);
	}
	if(ans!=sum){
		printf("please go home to sleep");
		Kafuu Chino;
	}
	e[pl].fl=0,e[pl+1].fl=0;ans=0;
	layer(t);
	while(dep[s]<t+1){
		cpy(head,cur,int,N);
		ISAP(s,INF,s,t);
	}
	for(int i=head[t];i;i=e[i].na) ans+=e[i].fl;
	printf("%d",ans);
}

P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

回归正题，或者说看道例题

题目描述

\(n\) 天 \(m\) 位少女，\(n\) 天之内为第 \(i\) 位少女拍摄至少 \(G_i\) 张图片

在第 \(i\) 天的时候，他有 \(C\) 个取材对象，在这天最多拍摄 \(D\) 张照片

当天对于第 \(i\) 个取材对象，拍摄的照片数必须在 \([l_i,r_i]\) 内

最大化照片拍摄数，如果没有可行解，输出 -1

建模方式

对于每一天设一个点 \(d_i\)，对于每位少女设一个点 \(g_i\)

源点向 \(d_i\) 连边，流量下界为 \(0\)，流量上界为每天最多拍摄的照片数

\(g_i\) 向汇点连边，流量上界为 \(\infty\)，流量下界为每个少女至少拍的照片数

对于当天每个取材对象 \(k\)，\(d_i\) 向 \(g_k\) 连边，容量即为 \([l_k,r_k]\)

然后跑有源汇上下界最大流即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 1000001
#define M 5001
#define INF 400000000
#define Kafuu return
#define Chino 0
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define int long long
#define R register
#define C const
using namespace std;
int G[N],dep[N],depn[N],n,stb,m,lo,ty,all,gal,mdpt,g,up,bas,head[N],cur[N],num=1,vs,vt,s,t,in[N],out[N],ans,fr,to,sum,pl;
bool yn;
struct Edge{
	int fl,na,np;
}e[N];
fx(void,add)(int f,int t,int fl){
	e[++num].na=head[f];
	e[num].np=t,e[num].fl=fl;
	head[f]=num;
}
fx(void,udadd)(int f,int t,int u,int d){
	add(f,t,u-d);add(t,f,0);
	in[t]+=d;out[f]+=d;
}
fx(int,gi)(){
	R char c=getchar();R int s=0,f=1;
	while(c>'9'||c<'0'){
		if(c=='-') f=-f;
		c=getchar();
	}
	while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
	return s*f;
}
queue<int>q;
fx(void,layer)(int t){
	set(dep,-1,int,N);set(depn,0,depn,1);
	dep[t]=0;depn[0]=1;int f;q.push(t);
	while(!q.empty()){
		f=q.front();q.pop();
		for(int i=head[f];i;i=e[i].na){
			if(dep[e[i].np]==-1){
				dep[e[i].np]=dep[f]+1;
				depn[dep[e[i].np]]+=1;
				q.push(e[i].np);
			}
		}
	}
}
fx(int,ISAP)(int now,int rf,int s,int t){
	if(now==t) return rf;
	int af=0,tf=0;
	for(int i=cur[now];i;i=e[i].na){
		cur[now]=i;
		if(!e[i].fl) continue;
		if(dep[e[i].np]==dep[now]-1){
			af=ISAP(e[i].np,min(e[i].fl,rf),s,t);
			if(af){
				e[i].fl-=af;e[i^1].fl+=af;
				tf+=af;rf-=af;
			}
			if(!rf) return tf;
		}
	}
	depn[dep[now]]-=1;
	if(!depn[dep[now]]) dep[s]=t+1;
	depn[++dep[now]]++;
	return tf;
}
signed main(){
	while(~scanf("%lld%lld",&n,&m)){
		set(e,0,e,1),set(head,0,head,1);num=1;yn=1;
		set(in,0,in,1),set(out,0,out,1);all=0,ans=0,sum=0;
		stb=n*m+n+m+1;
		s=stb+1,t=stb+2;vs=stb+3,vt=stb+4;
		bas=n+m+1;
		for(int i=1;i<=m;i++) G[i]=gi(),udadd(n+i,t,INF,G[i]);
		for(int day=1;day<=n;day++){
			gal=gi(),mdpt=gi();
			udadd(s,day,mdpt,0);
			for(g=1;g<=gal;g++){
				ty=gi(),lo=gi(),up=gi();
				udadd(day,bas+all+g,up,lo);
				udadd(bas+all+g,n+ty+1,INF,0);
			}
			all+=gal;
		}
		pl=num+1;udadd(t,s,INF,0);
		for(int i=1;i<=stb;i++){
			if(in[i]==out[i]) continue;
			else if(in[i]>out[i]){
				add(vs,i,in[i]-out[i]);
				add(i,vs,0);
				sum+=in[i]-out[i];
			} else {
				add(i,vt,out[i]-in[i]);
				add(vt,i,0);
			}
		}
		layer(vt);
		while(dep[vs]<vt+1){
			cpy(head,cur,int,N);
			ans+=ISAP(vs,INF,vs,vt);
		}
		e[pl].fl=0,e[pl+1].fl=0;ans=0;
		layer(t);
		while(dep[s]<t+1){
			cpy(head,cur,int,N);
			ISAP(s,INF,s,t);
		}
		for(int i=head[t];i;i=e[i].na){
			if(e[i].fl<G[e[i].np-n]){
				printf("-1\n\n");yn=0;
				break;
			}
		}
		if(!yn) continue;
		for(int i=head[t];i;i=e[i].na) ans+=e[i].fl;
		printf("%lld\n\n",ans);
	}
}

posted @ 2021-03-20 20:15 zythonc 阅读(197) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

zythonc

有源汇上下界最大流

无源汇上下界可行流

有源汇上下界最大流

P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流