浅谈建图优化 - 线段树优化
更新记录
【1】2020.10.16-20:40
- 1.完善内容
正文
在一些图论题中,我们可能会遇到一些题目让你对区间进行连边
这个时候如果我们暴力进行连边显然是会超时的
我们就要考虑有没有什么办法可以快速的进行区间连边
这个时候就要祭出区间操作的神器 - 线段树
线段树上的非叶节点表示的是区间,我们就可以直接对他们进行连边
举个例子,我们连一条 \(2\) 与区间 \([3,5]\) 之间的双向边
首先进行建树:
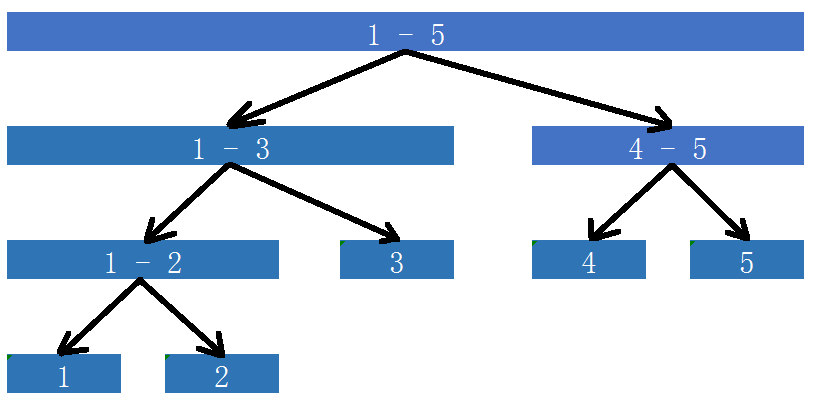
我们发现,如果只建一棵树的话,会出现访问错误
例如 \([mid+1,r]\) 会沿着区间错误的访问到 \([l,r]\)
所以我们正反边各建一棵线段树:

然后让叶节点没有入度的那棵线段树向节点 \(2\) 连一条单向边,然后从节点 \(2\) 向没有出度的那棵线段树连一条单向边
就像这样:
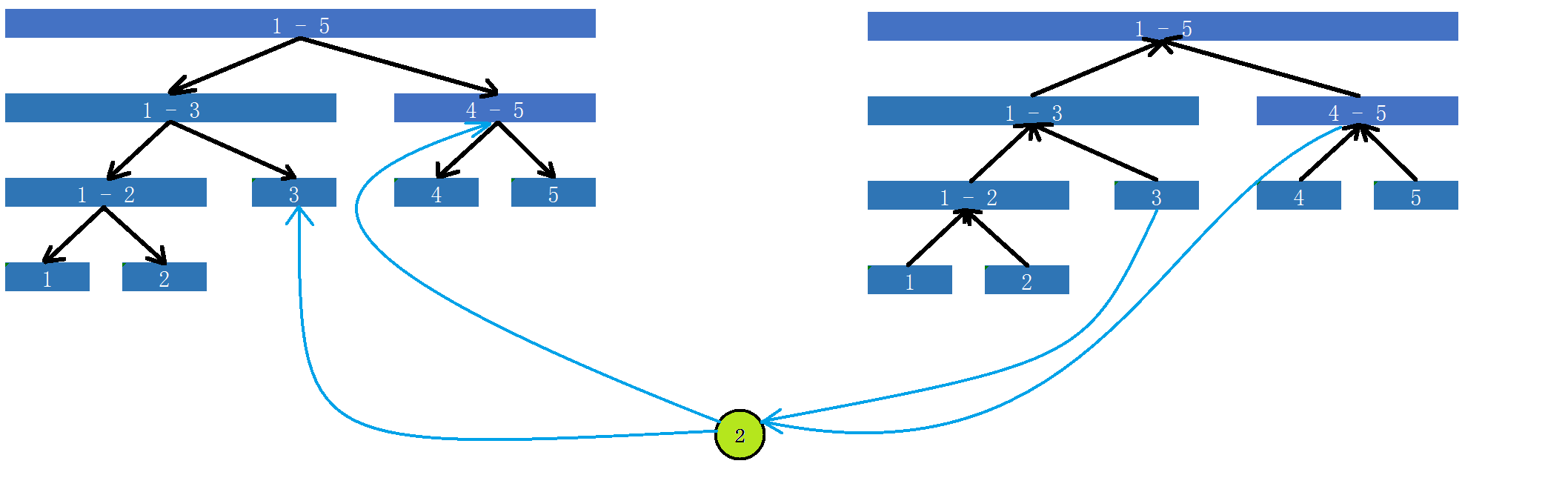
之后我们按照原来的套路进行操作即可
CF786B Legacy
【题意简化】
给你一个 \(n\) 个点的有向图,图上有 \(3\) 种边
- 1.\(u\to v\) 边权为 \(w\)
- 2.\(u\to[l,r]\) 边权为 \(w\)
- 3.\([l,r]\to u\) 边权为 \(w\)
求 \(s\) 点到所有点的最短路
这道题还算是有些麻烦,对于第一种边直接连接即可
第二种第三种就是将上面讲的双向边的连接拆成单向边进行连接
【代码实现】
#include<iostream>
#include<queue>
#include<cstring>
#define int long long
#define N 900004
#define M 5000050
using namespace std;
int n,q,s,num,head[N],dis[N],n2,n4,n8;
bool vis[N];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >que;
namespace in {int type,l,r,f,t,w;}
struct Edge {int na,np,w;} e[M];
struct segtree {int l,r;} t[N];
inline void add(int f,int t,int w=0){
e[++num].na=head[f];
e[num].np=t;e[num].w=w;
head[f]=num;
}
inline void dbadd(int f,int t,int w=0) {add(f,t,w);add(t,f,w);}
inline void tadd(int p,int plus=0,bool s=0) {
if(!s) add(p+plus,(p<<1)+plus),add(p+plus,(p<<1|1)+plus);
else add((p<<1)+plus,p+plus),add((p<<1|1)+plus,p+plus);
}
inline void build(int p,int l,int r){
t[p].l=l;t[p].r=r;
if(l==r){
dbadd(l+n8,p);
dbadd(l+n8,p+n4);
return;
}
tadd(p);tadd(p,n4,1);
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
}
inline void secadd(int p,int l,int r,int wp,int w,bool s){
if(t[p].l==l&&t[p].r==r){
if(!s) add(wp+n8,p,w);//s to p
else add(p+n4,wp+n8,w);
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) secadd(p<<1,l,r<mid?r:mid,wp,w,s);
if(r>mid) secadd(p<<1|1,mid+1<l?l:mid+1,r,wp,w,s);
}
inline void dij(){
memset(dis,0x7f,sizeof(dis));
dis[s]=0;que.push(make_pair(0,s));
while(!que.empty()){
int p=que.top().second;que.pop();
if(vis[p]) continue;
vis[p]=1;
for(int i=head[p];i;i=e[i].na){
if(dis[e[i].np]>dis[p]+e[i].w){
dis[e[i].np]=dis[p]+e[i].w;
que.push(make_pair(dis[e[i].np],e[i].np));
}
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>q>>s;
n2=n<<1;n4=n<<2;n8=n<<3;
build(1,1,n);
using namespace in;
for(int i=1;i<=q;i++){
cin>>type;
if(type==1){
cin>>f>>in::t>>w;
add(f+n8,in::t+n8,w);
}
else if(type==2){
cin>>f>>l>>r>>w;
secadd(1,l,r,f,w,0);
}
else{
cin>>in::t>>l>>r>>w;
secadd(1,l,r,in::t,w,1);
}
}
s+=n8;
dij();
for(int i=1,p=n8;i<=n;i++)
cout<<(dis[i+p]<1e18?dis[i+p]:-1)<<" \n"[i==n];
}
P6348 [PA2011]Journeys
这道题就是让我们区间对区间进行连边,然后求最短路
我们可以建两个虚点,然后这两个虚点之间的边的权值为 \(1\),其他的边均为 \(0\)
第一个区间连到第一个点上,第二个区间连到第二个点上
因为是双向边,我们连两次单项边即可
又因为这道题只有 \(0\) 与 \(1\) 两个权值,我们可以不用最短路,而直接用01BFS去求
【代码实现】
#include<iostream>
#include<cstring>
#include<queue>
#define N 10000006
using namespace std;
int n,m,p,fl,fr,tl,tr,n2,n4,n8,dis[N],head[N],num,nont[N],cnt;
struct Edge{int na,np,w;} e[N];
struct segtree{int l,r;} t[N];
deque<int>que;
inline void add(int f,int t,int w=0){
e[++num].na=head[f];
e[num].np=t;e[num].w=w;
head[f]=num;
}
inline void dbadd(int f,int t) {add(f,t);add(t,f);}
inline void build(int p,int l,int r){
t[p].l=l;t[p].r=r;
if(l==r){
nont[l]=p;
dbadd(p,p+n4);
return;
}
add(p,p<<1),add(p,p<<1|1);
add((p<<1)+n4,p+n4),add((p<<1|1)+n4,p+n4);
int mid=(l+r)>>1;
build(p<<1,l,mid);build(p<<1|1,mid+1,r);
}
inline void sadd(int p,int l,int r,int wp,bool s){
if(t[p].l==l&&t[p].r==r){
if(!s) add(wp,p);
else add(p+n4,wp);
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) sadd(p<<1,l,r<mid?r:mid,wp,s);
if(r>mid) sadd(p<<1|1,mid+1<l?l:mid+1,r,wp,s);
}
inline void dbsadd(int l1,int r1,int l2,int r2){
int p1=++cnt,p2=++cnt;
add(p2,p1,1);
sadd(1,l2,r2,p1,0);
sadd(1,l1,r1,p2,1);
p1=++cnt,p2=++cnt;
add(p2,p1,1);
sadd(1,l2,r2,p2,1);
sadd(1,l1,r1,p1,0);
}
inline void dij(){
memset(dis,0x3f,sizeof(dis));
dis[p]=0;que.push_front(p);
while(que.size()){
int bf=que.front();que.pop_front();
for(int i=head[bf];i;i=e[i].na){
if(dis[e[i].np]>dis[bf]+e[i].w){
dis[e[i].np]=dis[bf]+e[i].w;
if(!e[i].w) que.push_front(e[i].np);
else que.push_back(e[i].np);
}
}
}
}
signed main(){
cin>>n>>m>>p;
n2=n<<1;n4=n<<2;n8=n<<3;cnt=n8;
build(1,1,n);
for(int i=1;i<=m;i++){
cin>>fl>>fr>>tl>>tr;
dbsadd(fl,fr,tl,tr);
}
p=nont[p]+n4;
dij();
for(int i=1;i<=n;i++) cout<<dis[nont[i]]<<"\n";
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号