我们仍未知道那天所看见的题的解法 - 1
P1892 [BOI2003]团伙
【分析过程】
初看题面,直觉就告诉我这是一个并查集题
然后样例一遍秒了,接着开始口胡数据来做
最难考虑的是类似递归的情况,即\(x_1\)的敌人是\(x_2\),\(x_2\)的敌人是\(x_3\)……以此类推
这个时候考虑使用反集
在\(n\)个人中的,\(a\)与\(b\)是敌人,\(b\)与\(c\)是敌人,则会出现以下合并场面

用这张图可以考虑反集的正确性
【代码实现】
#include<iostream>
#include<cstdio>
using namespace std;
int fa[1000001],a,b,n,m,ans;
char c;
inline int find(int n){
if(fa[n]!=n) fa[n]=find(fa[n]);
return fa[n];
}
inline void unionn(int x,int y){
x=find(x),y=find(y);
fa[y]=x;
}
int main(){
cin>>n>>m;
for(int i=1;i<=(n<<1);++i){
fa[i]=i;
}
for(int i=1;i<=m;++i){
cin>>c>>a>>b;
if(c=='F') unionn(a,b);
else{
unionn(a,n+b);
unionn(b,n+a);
}
}
for(int i=1;i<=n;i++){
if(fa[i]==i) ans+=1;
}
printf("%d\n",ans);
}
【总结】
在并查集中时常考虑反集的使用
P6747 『MdOI R3』Teleport
【分析过程】
初看题面,这就是在求:
一开始可以按照异或的性质来做,实质上就是缩小枚举的区间
两个数异或必定大于的数为左端点,两个数必定小于的数为右端点
但是闭着眼睛都能想到能卡这个程序的数据
没有在二进制的层面考虑问题
考虑按位贪心
由于二进制运算都具有独立性,也就是说当某一位进行运算的时候其他的任何一位都不会受到影响
所以贪心是完全可行的
考虑二进制的运算法则,在每一位贪心的时候尽量选择1,否则就选0
由于存在不合法的情况,我们可以预处理0~n位的最小代价
【代码实现】
#include<iostream>
#include<cstdio>
#define int long long
#define N 1001000
using namespace std;
int wei[61],n,q,will,sum,ans,in,minn,amin[61];
inline int min(int a,int b){
return a>b?b:a;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>in;
for(int o=0;o<31;o++) wei[o]+=(bool)(in&(1ll<<o));
}
for(int i=0;i<=45;i++){
amin[i]=amin[i-1]+min(wei[i]*(1ll<<i),(n-wei[i])*(1ll<<i));
}
cin>>q;
while(q--){
cin>>will;
sum=0;ans=0;
if(will<amin[45]){
cout<<"-1\n";
continue;
}
for(int i=45;i>=0;i--){
if(sum+(1ll<<i)*(n-wei[i])+(i==0?0:amin[i-1])<=will){
sum+=(1ll<<i)*(n-wei[i]);
ans+=(1ll<<i);
}
else sum+=(1ll<<i)*wei[i];
}
cout<<ans<<"\n";
}
}
【总结】
对于二进制运算,一定要在二进制的层面想一想能否用到基础算法
CF1163F Indecisive Taxi Fee
【变量含义】
posdis[i]:i点到起点的最短路
invdis[i]:i点到终点的最短路
dis[i]:1到i的最短路
fr[i]:i这条边的起点
to[i]:i这条边的终点
w[i]:i这条边的权值
【分析过程】
对于原图,当某条边的权值被修改之后,图内的最短路的长度
首先思考暴力做法
很简单,修改之后跑最短路即可,时间复杂度爆炸
考虑一道图论题:求图上经过某一条边的最短路径
很简单吧?正向建边+反向建边,分别从起点与终点跑一次最短路,求出每个点到起点的最短路径与到终点的最短路径
答案就是:\(min(posdis[fr[i]]+invdis[to[i]]+w[i],posdis[to[i]]+inv[fr[i]]+w[i])\)
这么一想,似乎这个题可能用到这个思想
借助题解思考之后得到了接下来的思路
考虑特殊情况,当修改的边不在最短路上,并且这条边的权值被修改小了,我们就可以用这个方法比个大小,答案就出来了
这是一种情况
一提到“情况”这个词,不难发现这道题可以分类讨论
【情况一】当修改的边在最短路的路径上,并且权值被修改小了
【做法】直接输出起点到终点的最短路减去差值
【正确性】
- 本来就是最短路了,路径还被修改小了,那当然是最小的
【情况二】当修改的边不在最短路的路径上,并且权值被修改小了
【做法】比较这两条路径即可:\(min(dis[n],min(posdis[fr[i]]+invdis[to[i]]+w[i],posdis[to[i]]+inv[fr[i]]+w[i]))\)
【正确性】
- 没被修改之前所有的路径肯定都是大于等于最短路的值的,修改之后只有存在被修改的这条边的路径的最短路径的值发生了变化
- 这个路径有很多,但是我们关心的只是最小值,即经过这条边的最短路,由上可得做法正确
【情况三】当修改的边不在最短路的路径上,并且权值被修改大了
【做法】输出\(dis[n]\)即可
【正确性】
- 显然
【情况四】当修改的边在最短路的路径上,并且权值被修改大了
这种是最麻烦的,本来以为和k短路做法差不多,然后贪心就行了
结果发现还是我太弱了,因为次短路,次次短路都有可能经过这条边
当这条边被修改的时候,会影响很多路径
考虑从最终结果逆推,最后输出的答案肯定是\(dis[n]\)加上差值,然后与不经过这条边的最短路比个大小
区间操作啊...肯定是使用线段树维护啦
我们指定一条最短路径,然后用不在这条路径上的边去更新\([l,r]\)
例如边\(2\to4\),就可以更新蓝色区间:
红色边为最短路径
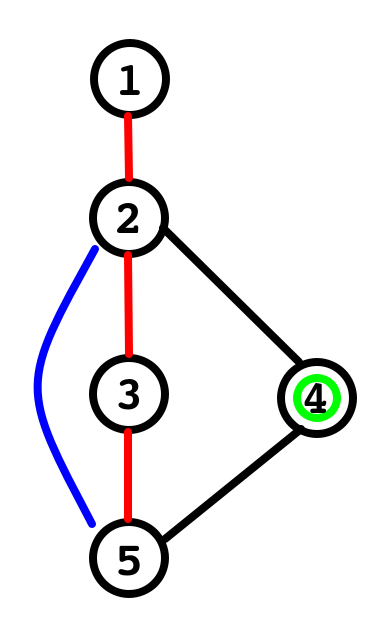
那\(l\)和\(r\)是?
对于一条绕过一条在最短路径上的边的路径
它肯定是在在原来的最短路径上的某个点\(p_1\)分叉,经过这条边,然后又在在原来的最短路径上的某个点\(p_2\)回来,例如:

(红色边路径为最短路)
当不经过边\(2\to6\)
可能从6分叉,沿橙色路径到5汇合,也可能直接沿蓝色路径从终点汇合
规定:
- 最短路径上的边的方向为到终点的方向
- 这里所说的入边为在最短路径上的边
\(l\)就是\(p_1\)的入边,\(r\)就是\(p_2\)的入边
当从\(5\)汇合时,边\(5\to8\)就能更新路径\(1\to6\to2\to3\to4\to5\)
也就是\(p_1\to p_2\)
没有写具体数值就是为了一图多用,能够模拟更多情况
诶,发现了没有,这就是问你经过某条指定边的最短路的时候顺便做的事情
最后查询即可
【代码实现】
#include<iostream>
#include<cstdio>
#include<queue>
#define int long long
#define N 1000001
#define INF 999999999999999
using namespace std;
int n,m,q,fr[N],to[N],w[N],bf,head[N],num,posdis[N],invdis[N],now,pathnum,ce,cv,ans,redge[N],pathnumrc[N],*toa,l[N],r[N];
bool on[N],vis[N];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >qu;
struct seg {int v;} t[N];
struct Edge {int fp,na,np,w;} e[N<<2];
inline int min(int a,int b){return a>b?b:a;}
inline void add(int f,int t,int w){
e[++num].na=head[f];
e[num].fp=f;e[num].np=t;e[num].w=w;
head[f]=num;
}
inline void dij(int s,int *pa,short sta){
for(int i=1;i<=n;i++) *(pa+i)=INF,vis[i]=0;
*(pa+s)=0;
qu.push(make_pair(0,s));
while(!qu.empty()){
bf=qu.top().second;qu.pop();
if(vis[bf]) continue;
vis[bf]=1;
for(int i=head[bf];i;i=e[i].na){
if(*(pa+bf)+e[i].w<*(pa+e[i].np)){
redge[e[i].np]=i;
*(pa+e[i].np)=*(pa+bf)+e[i].w;
qu.push(make_pair(*(pa+e[i].np),e[i].np));
if(!on[e[i].np]){
if(sta==1) l[e[i].np]=l[bf];
else if(sta==2) r[e[i].np]=r[bf];
}
}
}
}
}
inline void build(int node,int l,int r){
t[node].v=INF;
if(l==r) return;
int mid=(l+r)>>1;
build(node<<1,l,mid);
build(node<<1|1,mid+1,r);
}
inline void upd(int node,int fl,int fr,int ul,int ur,int v){
if(ul>ur) return;
if(ul<=fl&&fr<=ur){
t[node].v=min(t[node].v,v);
return;
}
int mid=(fl+fr)>>1;
if(ul<=mid) upd(node<<1,fl,mid,ul,ur,v);
if(mid<ur) upd(node<<1|1,mid+1,fr,ul,ur,v);
}
inline int query(int node,int l,int r,int rc){
if(l==r) return t[node].v;
int mid=(l+r)>>1,rans=t[node].v;
if(rc<=mid) rans=min(rans,query(node<<1,l,mid,rc));
else rans=min(rans,query(node<<1|1,mid+1,r,rc));
return rans;
}
signed main(){
scanf("%lld%lld%lld",&n,&m,&q);
for(int i=1;i<=m;i++){
scanf("%lld%lld%lld",&fr[i],&to[i],&w[i]);
add(fr[i],to[i],w[i]);
add(to[i],fr[i],w[i]);
pathnumrc[i]=pathnumrc[m+i]=-1;
}
toa=invdis;dij(n,toa,0);
on[1]=1;pathnum=l[1]=r[1]=0;now=1;
while(now!=n){
pathnumrc[redge[now]]=pathnum+1;
if(redge[now]%2) pathnumrc[redge[now]+1]=pathnum+1;
else pathnumrc[redge[now]-1]=pathnum+1;
pathnum+=1;
now=e[redge[now]].fp^e[redge[now]].np^now;
on[now]=1;l[now]=r[now]=pathnum;
}
toa=posdis;dij(1,toa,1);
toa=invdis;dij(n,toa,2);
build(1,1,pathnum);
for(int i=1;i<=num;i++)
if(pathnumrc[i]==-1)
upd(1,1,pathnum,l[e[i].fp]+1,r[e[i].np],posdis[e[i].fp]+invdis[e[i].np]+e[i].w);
for(int i=1;i<=q;i++){
scanf("%lld%lld",&ce,&cv);
ans=posdis[n];
if(pathnumrc[ce<<1]==-1){
if(cv<w[ce])
ans=min(ans,min(posdis[fr[ce]]+invdis[to[ce]],posdis[to[ce]]+invdis[fr[ce]])+cv);
}
else{
ans=ans-w[ce]+cv;
if(cv>w[ce]) ans=min(ans,query(1,1,pathnum,pathnumrc[ce<<1]));
}
printf("%lld\n",ans);
}
}
【答疑解惑】
针对阅读代码的时候可能产生的问题进行回答:
- 注意到我们将最短路径上的边进行了连续的标号处理,所以区间\([2,5]\)指的是最短路径上的第二条边到第五条边
- 因为有的时候边的起点与终点是反的,根据两个相同的数异或结果为0,0与任何数异或都为原数这些性质,我们自然能够正确的找到下一个\(now\)的位置
- 因为是双向边自然要有选择性的进行处理,例如乘二,判断奇偶等等
- 第一遍为啥是反着搜?——你正着试试
【后记】
真正理解了这道题,你是不是觉得很简单呢?
总结经验与教训,会对你有很大的帮助
欢迎Hack!!
CF1400E Clear the Multiset
【分析过程】
显然这道题相比于原来这种套路的题增加了一个操作:能将一个数直接减去 \(x\)
在一开始看题的时候可以直接想出这么一组数据:
3
4 5 6
显然这组数据的最小操作数为3
那么我们接着想什么时候能用操作一,以及用的时候有什么特点
设数列\(\{a_n\}\)
对于 \(1<=l<=r<=n\)
满足 \(r-l+1>min\{a_l\dots a_r\}\) (待验证,公式写于09.04)
则此时显然用操作一更好
那么我们发现,当 \([l,r]\) 用操作一更优的时候,我们一定一直用操作一直到不能再使用为止,正确性显然
那么此时我们就可以顺利的理清思路并写出代码:
#include<iostream>
#define N 2000001
using namespace std;
int n,a[N];
inline int doing(int l,int r){
if(l>r) return 0;
int minl=2147483647,p=0;
for(int i=l;i<=r;i++){
if(a[i]<minl){
minl=a[i];
p=i;
}
}
if(minl){
for(int i=l;i<=r;i++) a[i]-=minl;
}
return min(r-l+1,doing(l,p-1)+doing(p+1,r)+minl);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
return printf("%d",doing(1,n)),0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号