【Codeforces1263F_CF1263F】Economic Difficulties（图论_动态规划）

题目

Codeforces 1263F

翻译

好久没做英语大阅读了qwq。

题目名：经济难题

描述

贝兰宫的供电网络由两张电网组成：主电网和备用电网。宫殿中的导线是用贵金属制造的，所以卖掉一些是个好主意。

每张电网（主电网和备用电网）有一个根结点（标号为 \(1\) ）。其他所有结点都从根结点获取电力。每个结点到根有且只有一条路径。并且，两张电网都恰好有 \(n\) 个不会把电力继续向下输送的结点。

换句话说，每张电网都是一个恰好有 \(n\) 叶子的有根树，根的标号是 \(1\) 。两棵树的结点标号互相独立，且两棵树的结点之间不会相连。

宫殿中有 \(n\) 个用电设备。每个设备连接主电网的一个结点和备用电网的一个结点。用电设备只连接不会把电力继续向下输送的结点（即树的叶子）。每一个叶子恰好连接一个用电设备。

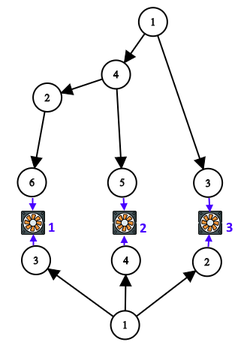
在这个例子中，主电网（上方的树）有 \(6\) 个结点，备用电网（下方的树）有 \(4\) 个结点。有 \(3\) 个用电设备，用蓝色数字编号。保证整个供电网络（两个电网和 \(n\) 个用电设备）可以用如下方式展示（就像上图中的一样）：

• 主电网是上方的树，导线从上向下连接；
• 备用电网是下方的树，导线从下向上连接；
• 用电设备在两棵树之间水平排成一排，从左到右编号依次为 \(1\) 到 \(n\) 。
• 结点之间的导线互不相交。

形式化地，对于每一棵树，存在一种从 \(1\) 号点开始的 DFS 序，叶子按照连接用电设备 \(1,2,\dots,n\) 的顺序访问（首先是连接了 \(1\) 号设备的叶子，然后是连接了 \(2\) 号设备的叶子，以此类推）。

毕斯内斯曼 商人想卖掉（删掉）最多的导线，使得每个用电设备仍然能被至少一个电网（主电网或备用电网）供电。换句话说，在主电网或备用电网中，每个设备应该至少存在一条到根结点的路径，并且这条路径只包含该电网的结点。

输入

第一行包含一个整数 \(n(1\leq n\leq 1000)\) —— 宫殿中用电设备的数量。

下一行包含一个整数 \(a(1+n\leq a \leq 1000+n)\) —— 主电网的结点数。

下一行包含 \(a-1\) 个整数 \(p_i(1\leq p_i\leq a)\) 。\(p_i\) 表示主电网中有一条导线连接 \(p_i\) 号结点和 \(i+1\) 号结点。

下一行包含 \(n\) 个整数 \(x_i\) —— 第 \(i\) 个设备在主电网中连接的结点编号。

下一行包含一个整数 \(b(1+n\leq b \leq 1000+n)\) —— 备用电网的结点数。

下一行包含 \(b-1\) 个整数 \(q_i(1\leq q_i\leq b)\) 。\(q_i\) 表示备用电网中有一条导线连接 \(q_i\) 号结点和 \(i+1\) 号结点。

下一行包含 \(n\) 个整数 \(y_i\) —— 第 \(i\) 个设备在备用电网中连接的结点编号。

保证每个电网都是一棵有 \(n\) 个叶子的树，每个叶子恰好连接一个设备。并且保证每棵树存在一种从 \(1\) 号点开始的 DFS 序，按照连接到的设备编号的顺序访问每个叶子。

输出

输出一个整数 —— 在保证所有设备都能供电的情况下最多能删掉的导线数量。

分析

我感觉很多不会这道题的人都是没看到 DFS 序那个条件 …… （比如某 s 姓选手）

删掉某棵树中的一条边时，无法供电的设备一定是这条边的子树中所连接的设备，也就是一个设备的区间。

由此能得到一个重要的性质：对于主电网，一个 极长的 不由它供电的区间 \([l,r]\) （即 \(l-1\) 和 \(r+1\) 如果存在均由主电网供电）对答案的贡献是一定的，与 \([1,l-1)\) 和 \((r+1,n]\) 是否由主电网供电无关。对备用电网也是如此。用 \(w_{0/1,l,r}\) 表示 \([l,r]\) 这段是不用主电网 / 备用电网供电的一个极长区间时，最多能删掉多少条边而不影响其他设备的电力供应。然后就可以直接 DP ：

\[f_i=\max_{j=0}^{i-1}(f_j+\max(w_{0,j+1,i},w_{1,j+1,i})) \]

考虑 \(w_{0,l,r}\) 怎么计算。枚举 \(l\) ，然后递推计算每一个 \(r\) 。和 \([l,r)\) 相比，\([l,r]\) 多删去的一定是 从 \(r\) 往上的一条链。为了让 \(l-1\) 不断电，这条链的末端不能高于 \(\mathrm{lca}(l-1,r)\)，同理也不能高于 \(\mathrm{lca}(r,r+1)\) 。事实上链的末端就是这两个 lca 中较低的一个，不可能有已经删过的，因为 \([l,r)\) 的方案中保证了 \(r\) 一定能供电，所以这一条链上删掉的点不会高于 \(\mathrm{lca}(r-1,r)\) 。具体可以画图和参考代码理解。

代码

#include <cstdio>
#include <cstring> 
#include <algorithm>
#include <vector>
using namespace std;
 
namespace zyt
{
	const int N = 1e3 + 10, P = 2e3 + 10, B = 15;
	int n, a, b, x[P], fa[B][P], dep[P], w[2][N][N];
	vector<int> g[P];
	void dfs(const int u)
	{
		dep[u] = dep[fa[0][u]] + 1;
		for (int i = 1; i < B; i++)
			fa[i][u] = fa[i - 1][fa[i - 1][u]];
		for (vector<int>::iterator it = g[u].begin(); it != g[u].end(); it++)
		{
			int v = *it;
			dfs(v);
		}
	}
	int lca(int a, int b)
	{
		if (!a || !b)
			return 1;
		if (dep[a] < dep[b])
			swap(a, b);
		for (int i = B - 1; i >= 0; i--)
			if (dep[fa[i][a]] >= dep[b])
				a = fa[i][a];
		if (a == b)
			return a;
		for (int i = B - 1; i >= 0; i--)
			if (fa[i][a] != fa[i][b])
				a = fa[i][a], b = fa[i][b];
		return fa[0][a];
	}
	void solve(const int p)
	{
		int m;
		scanf("%d", &m);
		for (int i = 1; i <= m; i++)
			g[i].clear();
		for (int i = 2; i <= m; i++)
			scanf("%d", fa[0] + i), g[fa[0][i]].push_back(i);
		dfs(1);
		for (int i = 1; i <= n; i++)
			scanf("%d", x + i);
		for (int i = 1; i <= n; i++)
		{
			for (int j = i; j <= n; j++)
			{
				int l = lca(x[j], x[i - 1]), l2 = lca(x[j], x[j + 1]);
				if (dep[l] < dep[l2])
					swap(l, l2);
				w[p][i][j] = w[p][i][j - 1] + dep[x[j]] - dep[l];
			}
		}
	}
	int dp[N];
	int work()
	{
		scanf("%d", &n);
		solve(0), solve(1);
		for (int i = 0; i < n; i++)
			for (int j = i + 1; j <= n; j++)
				dp[j] = max(dp[j], dp[i] + max(w[0][i + 1][j], w[1][i + 1][j]));
		printf("%d", dp[n]);
		return 0;
	}
}
int main()
{
	return zyt::work();
}