【博客】后缀自动机
后缀自动机
在阅读了众多大佬的博客之后 终于对后缀自动机有了初步理解 简单整理一下学习成果
大佬文献如下
史上最通俗的后缀自动机详解（写的真的好）
后缀自动机 (SAM) - OI Wiki （OI-wiki yyds）
引入
我们可以建立一个字典树 将原串的所有子串表示在一张有向无环图（DAG）上面
用一张大佬的图
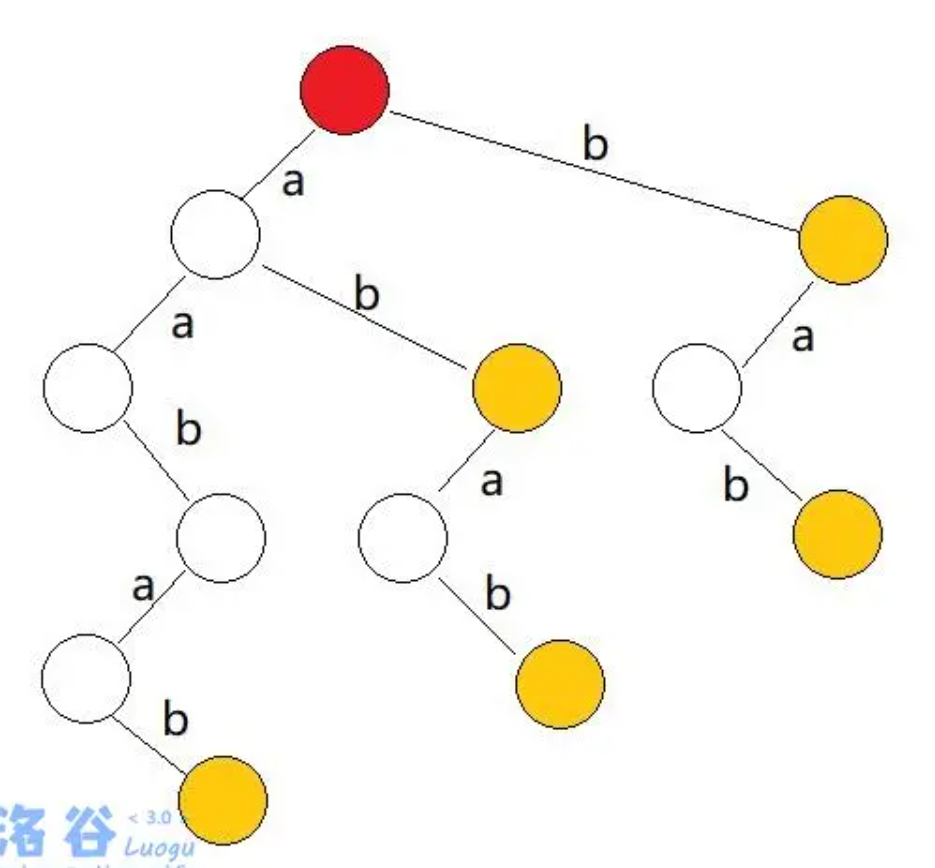
我们能够直观地总结出来的性质有：
- 有一个源点，若干个终止点。边代表在目前的字符串后加上的字母。从源点到任意一个节点的任意路径可以形成一个字符串。
- 从源点到任意节点的任意路径形成的字符串均为原串子串。从源点到任意节点的任意路径不能形成的字符串均不为原串子串。（简单来说，这个图可以表示，且仅可以表示出原串的所有子串)
- 从源点到任意终止节点的任意路径形成的字符串均为原串后缀。
- 从源点出发的任意两条不同路径形成的字符串不相同。
但是这样建立的DAG点数过多\(（n^2）\)
所以后缀自动机出现了
它建立的DAG把原DAG上的一些可以合并的点合并了
定义
结束位置endpos（学SAM离不开它）
对于一个子串，它在原串中可能出现在若干的位置。而一个子串\(p\)出现的这些位置的右端点标号组成的集合，我们称之为\(endpos(p)\)
例如原串为abcab时，$endpos(ab)={\ 2,5 \ }\ $
然后有很多性质
1.如果两个子串endpos的相同，则其中子串一个必然为另一个的后缀
2.对于任意两个字串 他们的endpos不是包含关系 就是交集为空的关系
3.对于endpos相同的子串，我们将它们归为一个endpos等价类。一个endpos等价类内的串的长度连续
4.endpos等价类的个数为O(n)
对于在p前添加一个字符，我们可以认为是对一个原集合进行分割，分割得到几个新的集合，且保留原集合。所有endpos等价类依靠这种分割关系，恰好可以构造出一个树形结构。于是类之间有了父子关系。这棵树便是parent tree，它是自动机的关键
还是大佬的图
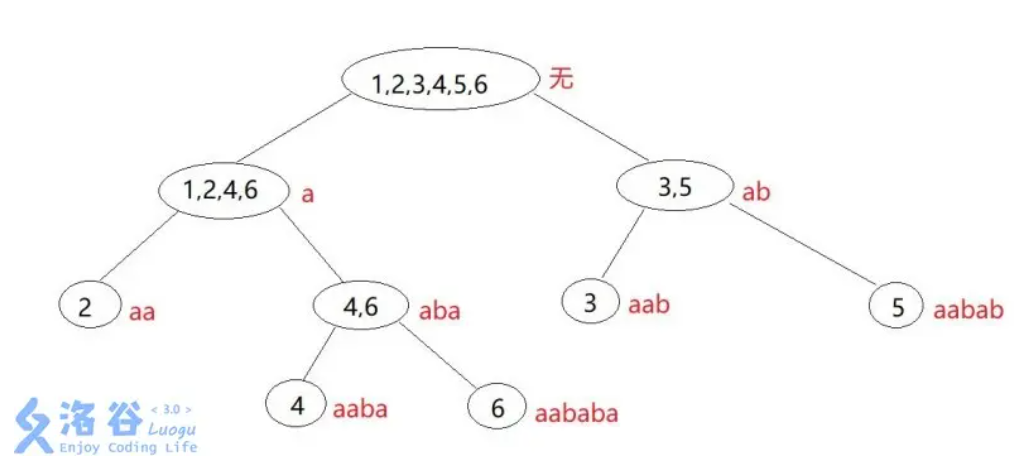
还有好多性质......
总之 这些性质保证了后缀自动机的可行性
再总之 我们最后建出的自动机有以下性质
- 有一个源点，边代表在当前字符串后增加一个字符。
- 每个点代表一个endpos等价类，到达一个点的路径形成的子串必须属于此点的类。
- 点之间有父子关系，到达点i的所有字符串的长度都必然大于到达fa(i)的所有字符串的长度，且到fa(i)的任意一字符串必为到达i的任意一字符串的后缀。
构造
构造的过程大概是这样的
假设我们新加入了边c
当前跳到的点为p
1.新建一个点 然后不断往父节点跳 （条件是不跳出根节点 并且p没有边c）跳到头有三种情况
2.分别处理三种情况
Case 1：p跳到了根节点 没有转移边c 那么连新点和根节点
Case2：p在有边c的点停下了 令q为p经过c到达的节点 且len(q)=len(p)+1 那么连新点和q
Case3：len(q)!=len(p)+1 将q裂开成新结点 继承父子关系
struct NODE
{
int ch[26];
int len,fa;
NODE(){memset(ch,0,sizeof(ch));len=0;}
}dian[MAXN<<1];
int las=1,tot=1;
void add(int c)
{
int p=las;int np=las=++tot;
dian[np].len=dian[p].len+1;
for(;p&&!dian[p].ch[c];p=dian[p].fa)dian[p].ch[c]=np; //不断跳
if(!p)dian[np].fa=1;//以上为case 1
else
{
int q=dian[p].ch[c];
if(dian[q].len==dian[p].len+1)dian[np].fa=q;//以上为case 2
else
{
int nq=++tot;dian[nq]=dian[q];
dian[nq].len=dian[p].len+1;
dian[q].fa=dian[np].fa=nq;
for(;p&&dian[p].ch[c]==q;p=dian[p].fa)dian[p].ch[c]=nq;//以上为case 3
}
}
}
char s[MAXN];int len;
int main()
{
scanf("%s",s);len=strlen(s);
for(int i=0;i<len;i++)add(s[i]-'a');
}
然后我们就建好了后缀自动机
它可以解决很多问题
比如判断A是否是B的子串 求不同子串的个数等
终！于！写！完！了！ （咆哮）
完结撒花
Let It Out - 陈奕迅 好好听
