沉淀再出发:使用python进行机器学习
沉淀再出发:使用python进行机器学习
一、前言
使用python进行学习运算和机器学习是非常方便的,因为其中有很多的库函数可以使用,同样的python自身语言的特点也非常利于程序的编写和使用。
二、几个简单的例子
2.1、使用python实现KNN算法
1 ######################################### 2 # kNN: k Nearest Neighbors 3 4 # Input: newInput: vector to compare to existing dataset (1xN) 5 # dataSet: size m data set of known vectors (NxM) 6 # labels: data set labels (1xM vector) 7 # k: number of neighbors to use for comparison 8 9 # Output: the most popular class label 10 ######################################### 11 12 from numpy import * 13 import operator 14 15 # create a dataset which contains 4 samples with 2 classes 16 def createDataSet(): 17 # create a matrix: each row as a sample 18 group = array([[1.0, 0.9], [1.0, 1.0], [0.1, 0.2], [0.0, 0.1]]) 19 labels = ['A', 'A', 'B', 'B'] # four samples and two classes 20 return group, labels 21 22 # classify using kNN 23 def kNNClassify(newInput, dataSet, labels, k): 24 numSamples = dataSet.shape[0] # shape[0] stands for the num of row 25 26 ## step 1: calculate Euclidean distance 27 # tile(A, reps): Construct an array by repeating A reps times 28 # the following copy numSamples rows for dataSet 29 diff = tile(newInput, (numSamples, 1)) - dataSet # Subtract element-wise 30 squaredDiff = diff ** 2 # squared for the subtract 31 squaredDist = sum(squaredDiff, axis = 1) # sum is performed by row 32 distance = squaredDist ** 0.5 33 34 ## step 2: sort the distance 35 # argsort() returns the indices that would sort an array in a ascending order 36 sortedDistIndices = argsort(distance) 37 38 classCount = {} # define a dictionary (can be append element) 39 for i in range(k): 40 ## step 3: choose the min k distance 41 voteLabel = labels[sortedDistIndices[i]] 42 43 ## step 4: count the times labels occur 44 # when the key voteLabel is not in dictionary classCount, get() 45 # will return 0 46 classCount[voteLabel] = classCount.get(voteLabel, 0) + 1 47 48 ## step 5: the max voted class will return 49 maxCount = 0 50 for key, value in classCount.items(): 51 if value > maxCount: 52 maxCount = value 53 maxIndex = key 54 55 return maxIndex
测试文件:
1 import knn 2 from numpy import * 3 4 dataSet, labels = knn.createDataSet() 5 6 testX = array([1.2, 1.0]) 7 k = 3 8 k = 3 9 outputLabel = knn.kNNClassify(testX, dataSet, labels, 3) 10 print ("Your input is:", testX, "and classified to class: ", outputLabel) 11 12 testX = array([0.1, 0.3]) 13 outputLabel = knn.kNNClassify(testX, dataSet, labels, 3) 14 print ("Your input is:", testX, "and classified to class: ", outputLabel)
其中knn的思路非常简单,就是在某一个范围内观察距离该需要归类的样本的所有样本之中,那一个种类的样本数目最多,通过对附近的K个样本的寻找来进行分类。

2.2、使用scikit-learn库进行机器学习
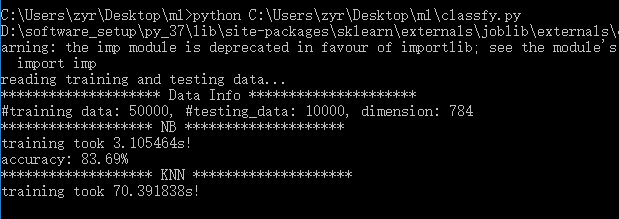
1 #!usr/bin/env python 2 # coding:utf-8 3 4 import sys 5 import os 6 import time 7 from sklearn import metrics 8 import numpy as np 9 import pickle 10 # import imp 11 12 # imp.reload(sys) 13 14 15 # Multinomial Naive Bayes Classifier 16 def naive_bayes_classifier(train_x, train_y): 17 from sklearn.naive_bayes import MultinomialNB 18 model = MultinomialNB(alpha=0.01) 19 model.fit(train_x, train_y) 20 return model 21 22 23 # KNN Classifier 24 def knn_classifier(train_x, train_y): 25 from sklearn.neighbors import KNeighborsClassifier 26 model = KNeighborsClassifier() 27 model.fit(train_x, train_y) 28 return model 29 30 31 # Logistic Regression Classifier 32 def logistic_regression_classifier(train_x, train_y): 33 from sklearn.linear_model import LogisticRegression 34 model = LogisticRegression(penalty='l2') 35 model.fit(train_x, train_y) 36 return model 37 38 39 # Random Forest Classifier 40 def random_forest_classifier(train_x, train_y): 41 from sklearn.ensemble import RandomForestClassifier 42 model = RandomForestClassifier(n_estimators=8) 43 model.fit(train_x, train_y) 44 return model 45 46 47 # Decision Tree Classifier 48 def decision_tree_classifier(train_x, train_y): 49 from sklearn import tree 50 model = tree.DecisionTreeClassifier() 51 model.fit(train_x, train_y) 52 return model 53 54 55 # GBDT(Gradient Boosting Decision Tree) Classifier 56 def gradient_boosting_classifier(train_x, train_y): 57 from sklearn.ensemble import GradientBoostingClassifier 58 model = GradientBoostingClassifier(n_estimators=200) 59 model.fit(train_x, train_y) 60 return model 61 62 63 # SVM Classifier 64 def svm_classifier(train_x, train_y): 65 from sklearn.svm import SVC 66 model = SVC(kernel='rbf', probability=True) 67 model.fit(train_x, train_y) 68 return model 69 70 # SVM Classifier using cross validation 71 def svm_cross_validation(train_x, train_y): 72 from sklearn.grid_search import GridSearchCV 73 from sklearn.svm import SVC 74 model = SVC(kernel='rbf', probability=True) 75 param_grid = {'C': [1e-3, 1e-2, 1e-1, 1, 10, 100, 1000], 'gamma': [0.001, 0.0001]} 76 grid_search = GridSearchCV(model, param_grid, n_jobs = 1, verbose=1) 77 grid_search.fit(train_x, train_y) 78 best_parameters = grid_search.best_estimator_.get_params() 79 for para, val in best_parameters.items(): 80 print (para, val) 81 model = SVC(kernel='rbf', C=best_parameters['C'], gamma=best_parameters['gamma'], probability=True) 82 model.fit(train_x, train_y) 83 return model 84 85 def read_data(data_file): 86 import gzip 87 f = gzip.open(data_file, "rb") 88 train, val, test = pickle.load(f,encoding='bytes') 89 f.close() 90 train_x = train[0] 91 train_y = train[1] 92 test_x = test[0] 93 test_y = test[1] 94 return train_x, train_y, test_x, test_y 95 96 if __name__ == '__main__': 97 data_file = "mnist.pkl.gz" 98 thresh = 0.5 99 model_save_file = None 100 model_save = {} 101 102 test_classifiers = ['NB', 'KNN', 'LR', 'RF', 'DT', 'SVM', 'GBDT'] 103 classifiers = {'NB':naive_bayes_classifier, 104 'KNN':knn_classifier, 105 'LR':logistic_regression_classifier, 106 'RF':random_forest_classifier, 107 'DT':decision_tree_classifier, 108 'SVM':svm_classifier, 109 'SVMCV':svm_cross_validation, 110 'GBDT':gradient_boosting_classifier 111 } 112 113 print ('reading training and testing data...') 114 train_x, train_y, test_x, test_y = read_data(data_file) 115 num_train, num_feat = train_x.shape 116 num_test, num_feat = test_x.shape 117 is_binary_class = (len(np.unique(train_y)) == 2) 118 print ('******************** Data Info *********************') 119 print ('#training data: %d, #testing_data: %d, dimension: %d' % (num_train, num_test, num_feat)) 120 121 for classifier in test_classifiers: 122 print ('******************* %s ********************' % classifier) 123 start_time = time.time() 124 model = classifiers[classifier](train_x, train_y) 125 print ('training took %fs!' % (time.time() - start_time)) 126 predict = model.predict(test_x) 127 if model_save_file != None: 128 model_save[classifier] = model 129 if is_binary_class: 130 precision = metrics.precision_score(test_y, predict) 131 recall = metrics.recall_score(test_y, predict) 132 print ('precision: %.2f%%, recall: %.2f%%' % (100 * precision, 100 * recall)) 133 accuracy = metrics.accuracy_score(test_y, predict) 134 print ('accuracy: %.2f%%' % (100 * accuracy) ) 135 136 if model_save_file != None: 137 pickle.dump(model_save, open(model_save_file, 'wb'))
其中数据集使用的minst数据集。
2.3、sklearn的使用
1 Supervised Learning 2 Classification 3 Regression 4 Measuring performance 5 Unsupervised Learning 6 Clustering 7 Dimensionality Reduction 8 Density Estimation 9 Evaluation of Learning Models 10 Choosing the right algorithm for your dataset
2.3.1、分类任务(随机梯度下降(SGD)算法)
1 >>> import matplotlib.pyplot as plt 2 >>> plt.style.use('seaborn') 3 >>> from fig_code import plot_sgd_separator 4 >>> plot_sgd_separator() 5 >>> plt.show()
其中sgd_separator.py:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from sklearn.linear_model import SGDClassifier 4 from sklearn.datasets.samples_generator import make_blobs 5 6 def plot_sgd_separator(): 7 # we create 50 separable points 8 X, Y = make_blobs(n_samples=50, centers=2, 9 random_state=0, cluster_std=0.60) 10 11 # fit the model 12 clf = SGDClassifier(loss="hinge", alpha=0.01, 13 max_iter=200, fit_intercept=True) 14 clf.fit(X, Y) 15 16 # plot the line, the points, and the nearest vectors to the plane 17 xx = np.linspace(-1, 5, 10) 18 yy = np.linspace(-1, 5, 10) 19 20 X1, X2 = np.meshgrid(xx, yy) 21 Z = np.empty(X1.shape) 22 for (i, j), val in np.ndenumerate(X1): 23 x1 = val 24 x2 = X2[i, j] 25 p = clf.decision_function(np.array([x1, x2]).reshape(1, -1)) 26 Z[i, j] = p[0] 27 levels = [-1.0, 0.0, 1.0] 28 linestyles = ['dashed', 'solid', 'dashed'] 29 colors = 'k' 30 31 ax = plt.axes() 32 ax.contour(X1, X2, Z, levels, colors=colors, linestyles=linestyles) 33 ax.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired) 34 35 ax.axis('tight') 36 37 38 if __name__ == '__main__': 39 plot_sgd_separator() 40 plt.show()

2.3.2、线性回归任务
@1、linear_regression.py:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from sklearn.linear_model import LinearRegression 4 5 6 def plot_linear_regression(): 7 a = 0.5 8 b = 1.0 9 10 # x from 0 to 10 11 x = 30 * np.random.random(20) 12 13 # y = a*x + b with noise 14 y = a * x + b + np.random.normal(size=x.shape) 15 16 # create a linear regression classifier 17 clf = LinearRegression() 18 clf.fit(x[:, None], y) 19 20 # predict y from the data 21 x_new = np.linspace(0, 30, 100) 22 y_new = clf.predict(x_new[:, None]) 23 24 # plot the results 25 ax = plt.axes() 26 ax.scatter(x, y) 27 ax.plot(x_new, y_new) 28 29 ax.set_xlabel('x') 30 ax.set_ylabel('y') 31 32 ax.axis('tight') 33 34 35 if __name__ == '__main__': 36 plot_linear_regression() 37 plt.show()
导入上面的程序并使用:
1 >>> from fig_code import plot_linear_regression 2 >>> plot_linear_regression() 3 >>> plt.show()
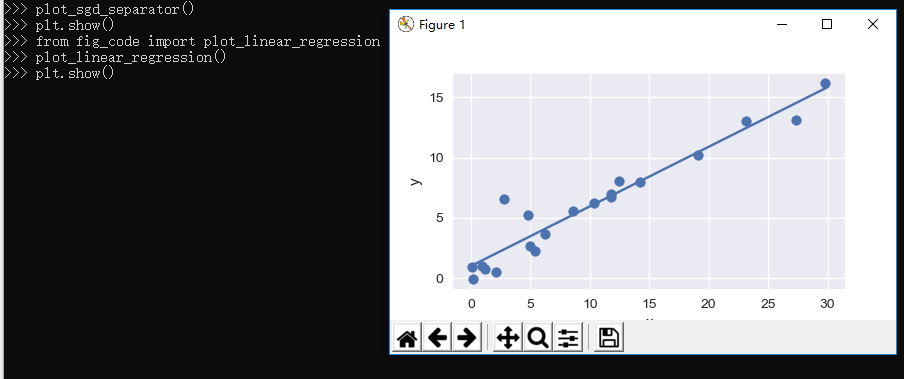
@2、接下来我们自己生成数据并进行拟合:
生成模型:
1 >>> from sklearn.linear_model import LinearRegression 2 >>> model = LinearRegression(normalize=True) 3 >>> print(model.normalize) 4 True 5 >>> print(model) 6 LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True)
生成数据:
1 >>> x = np.arange(10) 2 >>> y = 2 * x + 1 3 >>> print(x) 4 [0 1 2 3 4 5 6 7 8 9] 5 >>> print(y) 6 [ 1 3 5 7 9 11 13 15 17 19] 7 >>> plt.plot(x, y, 'o'); 8 [<matplotlib.lines.Line2D object at 0x0000020B141025F8>] 9 >>> plt.show() 10 >>>
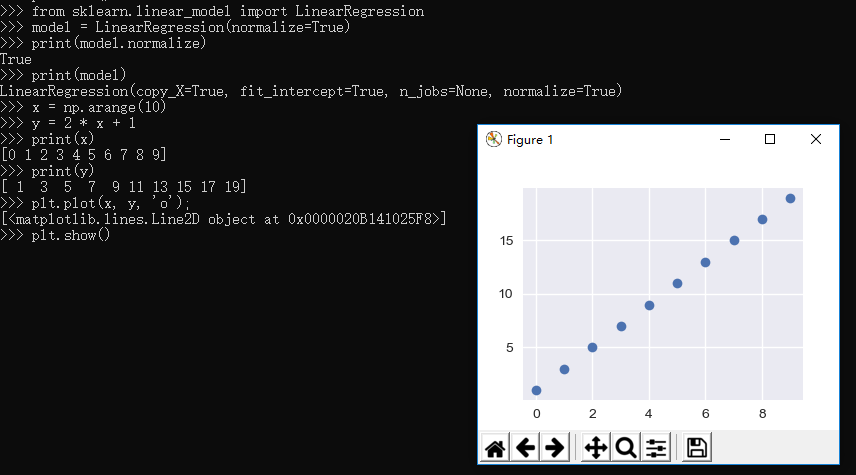
进行拟合:
1 >>> X = x[:, np.newaxis] 2 >>> print(X) 3 [[0] 4 [1] 5 [2] 6 [3] 7 [4] 8 [5] 9 [6] 10 [7] 11 [8] 12 [9]] 13 >>> print(y) 14 [ 1 3 5 7 9 11 13 15 17 19] 15 >>> model.fit(X, y) 16 LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True) 17 >>> print(model.coef_) 18 [2.] 19 >>> print(model.intercept_) 20 0.9999999999999982 21 >>>
可以看到斜率和截距确实是我们期望的。
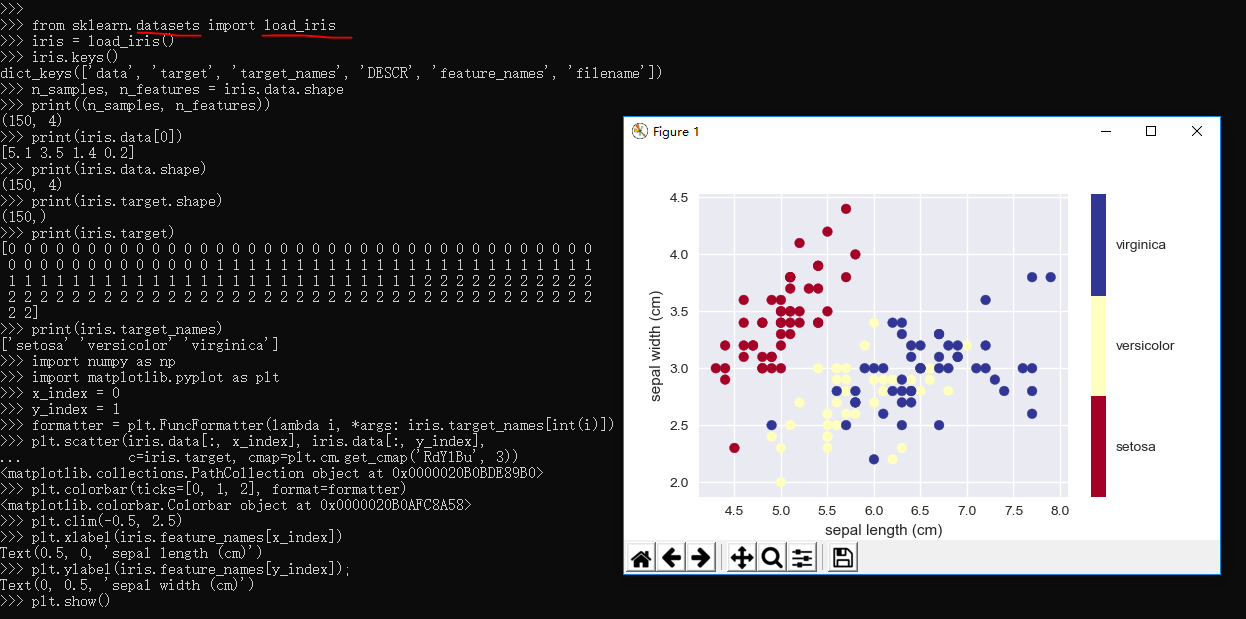
2.3.3、Iris Dataset的简单样例
1 >>> from sklearn.datasets import load_iris 2 >>> iris = load_iris() 3 >>> iris.keys() 4 dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']) 5 >>> n_samples, n_features = iris.data.shape 6 >>> print((n_samples, n_features)) 7 (150, 4) 8 >>> print(iris.data[0]) 9 [5.1 3.5 1.4 0.2] 10 >>> print(iris.data.shape) 11 (150, 4) 12 >>> print(iris.target.shape) 13 (150,) 14 >>> print(iris.target) 15 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 16 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 17 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 18 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 19 2 2] 20 >>> print(iris.target_names) 21 ['setosa' 'versicolor' 'virginica'] 22 >>> import numpy as np 23 >>> import matplotlib.pyplot as plt 24 >>> x_index = 0 25 >>> y_index = 1 26 >>> formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)]) 27 >>> plt.scatter(iris.data[:, x_index], iris.data[:, y_index], 28 ... c=iris.target, cmap=plt.cm.get_cmap('RdYlBu', 3)) 29 <matplotlib.collections.PathCollection object at 0x0000020B0BDE89B0> 30 >>> plt.colorbar(ticks=[0, 1, 2], format=formatter) 31 <matplotlib.colorbar.Colorbar object at 0x0000020B0AFC8A58> 32 >>> plt.clim(-0.5, 2.5) 33 >>> plt.xlabel(iris.feature_names[x_index]) 34 Text(0.5, 0, 'sepal length (cm)') 35 >>> plt.ylabel(iris.feature_names[y_index]); 36 Text(0, 0.5, 'sepal width (cm)') 37 >>> plt.show() 38 >>>
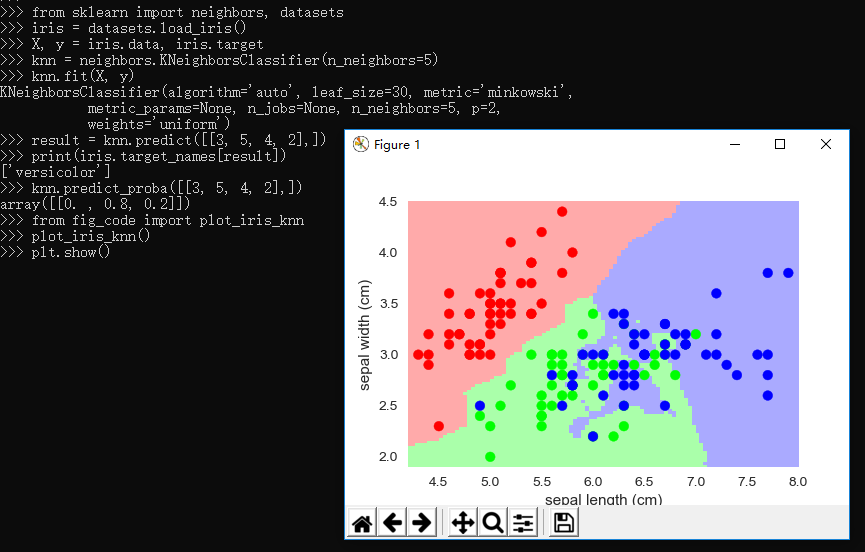
2.3.4、knn分类器
1 """ 2 Small helpers for code that is not shown in the notebooks 3 """ 4 5 from sklearn import neighbors, datasets, linear_model 6 import pylab as pl 7 import numpy as np 8 from matplotlib.colors import ListedColormap 9 10 # Create color maps for 3-class classification problem, as with iris 11 cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) 12 cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF']) 13 14 def plot_iris_knn(): 15 iris = datasets.load_iris() 16 X = iris.data[:, :2] # we only take the first two features. We could 17 # avoid this ugly slicing by using a two-dim dataset 18 y = iris.target 19 20 knn = neighbors.KNeighborsClassifier(n_neighbors=3) 21 knn.fit(X, y) 22 23 x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1 24 y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1 25 xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), 26 np.linspace(y_min, y_max, 100)) 27 Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]) 28 29 # Put the result into a color plot 30 Z = Z.reshape(xx.shape) 31 pl.figure() 32 pl.pcolormesh(xx, yy, Z, cmap=cmap_light) 33 34 # Plot also the training points 35 pl.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold) 36 pl.xlabel('sepal length (cm)') 37 pl.ylabel('sepal width (cm)') 38 pl.axis('tight') 39 40 41 def plot_polynomial_regression(): 42 rng = np.random.RandomState(0) 43 x = 2*rng.rand(100) - 1 44 45 f = lambda t: 1.2 * t**2 + .1 * t**3 - .4 * t **5 - .5 * t ** 9 46 y = f(x) + .4 * rng.normal(size=100) 47 48 x_test = np.linspace(-1, 1, 100) 49 50 pl.figure() 51 pl.scatter(x, y, s=4) 52 53 X = np.array([x**i for i in range(5)]).T 54 X_test = np.array([x_test**i for i in range(5)]).T 55 regr = linear_model.LinearRegression() 56 regr.fit(X, y) 57 pl.plot(x_test, regr.predict(X_test), label='4th order') 58 59 X = np.array([x**i for i in range(10)]).T 60 X_test = np.array([x_test**i for i in range(10)]).T 61 regr = linear_model.LinearRegression() 62 regr.fit(X, y) 63 pl.plot(x_test, regr.predict(X_test), label='9th order') 64 65 pl.legend(loc='best') 66 pl.axis('tight') 67 pl.title('Fitting a 4th and a 9th order polynomial') 68 69 pl.figure() 70 pl.scatter(x, y, s=4) 71 pl.plot(x_test, f(x_test), label="truth") 72 pl.axis('tight') 73 pl.title('Ground truth (9th order polynomial)')
引用上面的包:
1 >>> from sklearn import neighbors, datasets 2 >>> iris = datasets.load_iris() 3 >>> X, y = iris.data, iris.target 4 >>> knn = neighbors.KNeighborsClassifier(n_neighbors=5) 5 >>> knn.fit(X, y) 6 KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', 7 metric_params=None, n_jobs=None, n_neighbors=5, p=2, 8 weights='uniform') 9 >>> result = knn.predict([[3, 5, 4, 2],]) 10 >>> print(iris.target_names[result]) 11 ['versicolor'] 12 >>> knn.predict_proba([[3, 5, 4, 2],]) 13 array([[0. , 0.8, 0.2]]) 14 >>> from fig_code import plot_iris_knn 15 >>> plot_iris_knn() 16 >>> plt.show() 17 >>>
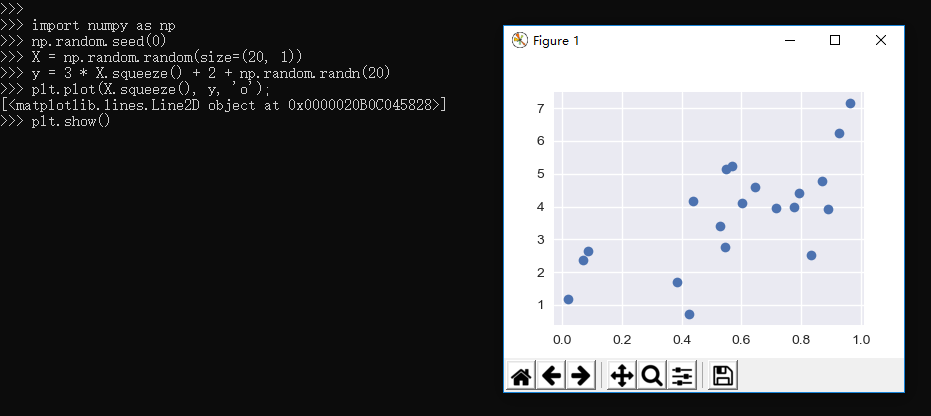
2.3.5、Regression Example
1 >>> import numpy as np 2 >>> np.random.seed(0) 3 >>> X = np.random.random(size=(20, 1)) 4 >>> y = 3 * X.squeeze() + 2 + np.random.randn(20) 5 >>> plt.plot(X.squeeze(), y, 'o'); 6 [<matplotlib.lines.Line2D object at 0x0000020B0C045828>] 7 >>> plt.show()
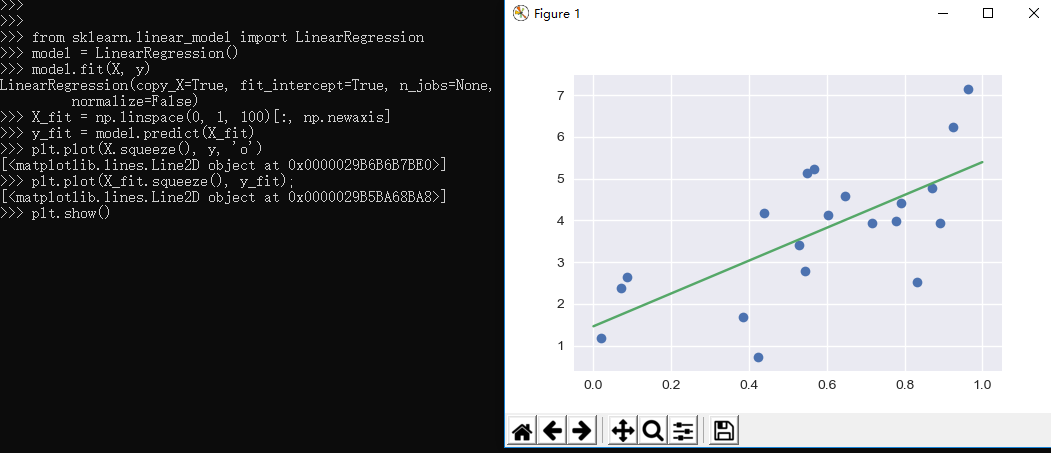
1 >>> 2 >>> from sklearn.linear_model import LinearRegression 3 >>> model = LinearRegression() 4 >>> model.fit(X, y) 5 LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, 6 normalize=False) 7 >>> X_fit = np.linspace(0, 1, 100)[:, np.newaxis] 8 >>> y_fit = model.predict(X_fit) 9 >>> plt.plot(X.squeeze(), y, 'o') 10 [<matplotlib.lines.Line2D object at 0x0000029B6B6B7BE0>] 11 >>> plt.plot(X_fit.squeeze(), y_fit); 12 [<matplotlib.lines.Line2D object at 0x0000029B5BA68BA8>] 13 >>> plt.show()
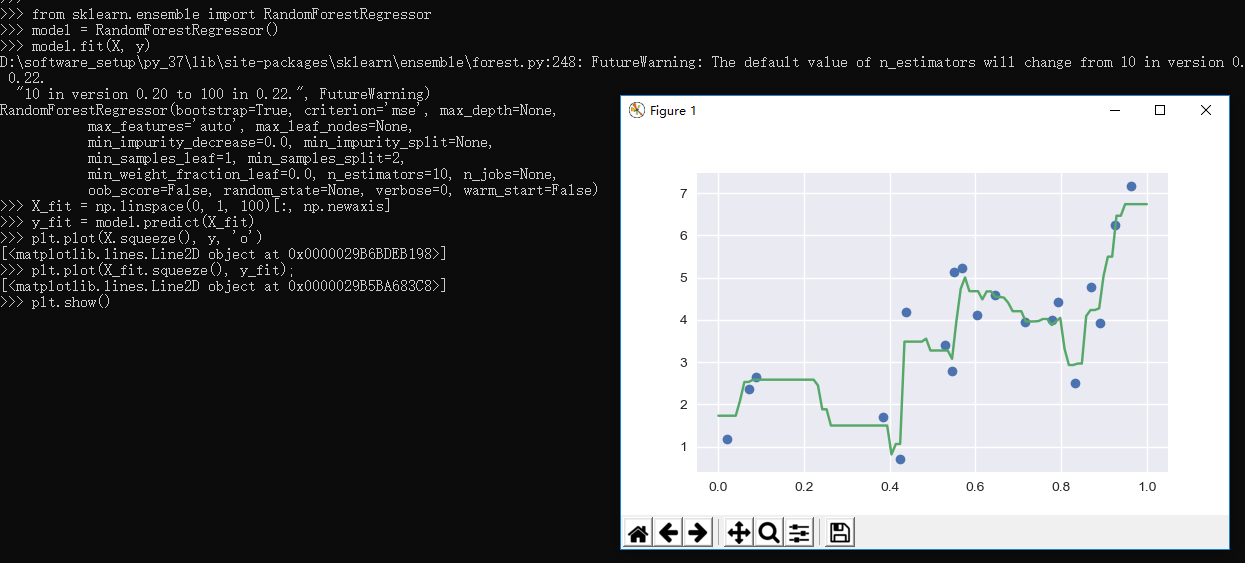
Scikit-learn also has some more sophisticated models, which can respond to finer features in the data::
1 >>> from sklearn.ensemble import RandomForestRegressor 2 >>> model = RandomForestRegressor() 3 >>> model.fit(X, y) 4 FutureWarning: The default value of n_estimators will change from 10 in version 0.20 to 100 in 0.22. 5 "10 in version 0.20 to 100 in 0.22.", FutureWarning) 6 RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None, 7 max_features='auto', max_leaf_nodes=None, 8 min_impurity_decrease=0.0, min_impurity_split=None, 9 min_samples_leaf=1, min_samples_split=2, 10 min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=None, 11 oob_score=False, random_state=None, verbose=0, warm_start=False) 12 >>> X_fit = np.linspace(0, 1, 100)[:, np.newaxis] 13 >>> y_fit = model.predict(X_fit) 14 >>> plt.plot(X.squeeze(), y, 'o') 15 [<matplotlib.lines.Line2D object at 0x0000029B6BDEB198>] 16 >>> plt.plot(X_fit.squeeze(), y_fit); 17 [<matplotlib.lines.Line2D object at 0x0000029B5BA683C8>] 18 >>> plt.show() 19 >>>
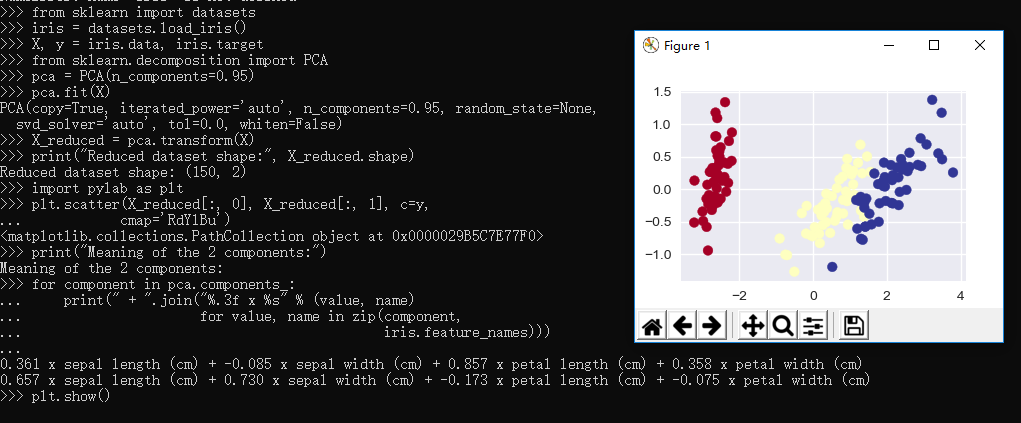
2.3.6、Dimensionality Reduction: PCA
1 >>> from sklearn import datasets 2 >>> iris = datasets.load_iris() 3 >>> X, y = iris.data, iris.target 4 >>> from sklearn.decomposition import PCA 5 >>> pca = PCA(n_components=0.95) 6 >>> pca.fit(X) 7 PCA(copy=True, iterated_power='auto', n_components=0.95, random_state=None, 8 svd_solver='auto', tol=0.0, whiten=False) 9 >>> X_reduced = pca.transform(X) 10 >>> print("Reduced dataset shape:", X_reduced.shape) 11 Reduced dataset shape: (150, 2) 12 >>> import pylab as plt 13 >>> plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, 14 ... cmap='RdYlBu') 15 <matplotlib.collections.PathCollection object at 0x0000029B5C7E77F0> 16 >>> print("Meaning of the 2 components:") 17 Meaning of the 2 components: 18 >>> for component in pca.components_: 19 ... print(" + ".join("%.3f x %s" % (value, name) 20 ... for value, name in zip(component, 21 ... iris.feature_names))) 22 ... 23 0.361 x sepal length (cm) + -0.085 x sepal width (cm) + 0.857 x petal length (cm) + 0.358 x petal width (cm) 24 0.657 x sepal length (cm) + 0.730 x sepal width (cm) + -0.173 x petal length (cm) + -0.075 x petal width (cm) 25 >>> plt.show() 26 >>>
2.3.7、Clustering: K-means
1 >>> from sklearn.cluster import KMeans 2 >>> k_means = KMeans(n_clusters=3, random_state=0) # Fixing the RNG in kmeans 3 >>> k_means.fit(X) 4 KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300, 5 n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto', 6 random_state=0, tol=0.0001, verbose=0) 7 >>> y_pred = k_means.predict(X) 8 >>> plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y_pred, 9 ... cmap='RdYlBu'); 10 <matplotlib.collections.PathCollection object at 0x0000029B5C7456A0> 11 >>> plt.show() 12 >>>

2.4、sklearn的模型验证
An important piece of machine learning is model validation: that is, determining how well your model will generalize from the training data
to future unlabeled data. Let's look at an example using the nearest neighbor classifier. This is a very simple classifier:
it simply stores all training data, and for any unknown quantity, simply returns the label of the closest training point.With the iris data,
it very easily returns the correct prediction for each of the input points:
样例如下:
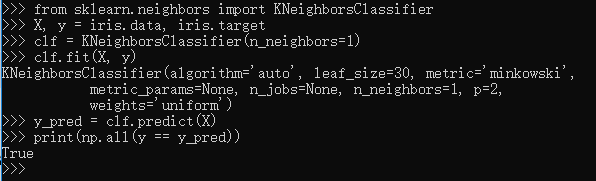
1 >>> from sklearn.neighbors import KNeighborsClassifier 2 >>> X, y = iris.data, iris.target 3 >>> clf = KNeighborsClassifier(n_neighbors=1) 4 >>> clf.fit(X, y) 5 KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', 6 metric_params=None, n_jobs=None, n_neighbors=1, p=2, 7 weights='uniform') 8 >>> y_pred = clf.predict(X) 9 >>> print(np.all(y == y_pred)) 10 True 11 >>>
A more useful way to look at the results is to view the confusion matrix, or the matrix showing the frequency of inputs and outputs:
>>> from sklearn.metrics import confusion_matrix >>> print(confusion_matrix(y, y_pred)) [[50 0 0] [ 0 50 0] [ 0 0 50]]
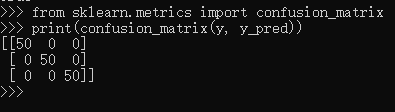
For each class, all 50 training samples are correctly identified. But this does not mean that our model is perfect! In particular, such a model generalizes extremely poorly to new data. We can simulate this by splitting our data into a training set and a testing set. Scikit-learn contains some convenient routines to do this:
>>> from sklearn.model_selection import train_test_split >>> Xtrain, Xtest, ytrain, ytest = train_test_split(X, y) >>> clf.fit(Xtrain, ytrain) KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=None, n_neighbors=1, p=2, weights='uniform') >>> ypred = clf.predict(Xtest) >>> print(confusion_matrix(ytest, ypred)) [[12 0 0] [ 0 6 0] [ 0 2 18]]
This paints a better picture of the true performance of our classifier: apparently there is some confusion between the second and third species, which we might anticipate given what we've seen of the data above.This is why it's extremely important to use a train/test split when evaluating your models.



