乘风破浪：LeetCode真题_031_Next Permutation

乘风破浪：LeetCode真题_031_Next Permutation

一、前言

    这是一道经典的题目，我们实在想不出最好的方法，只能按照已有的方法来解决，同时我们也应该思考一下为什么要这样做？是怎么想到的？这比我们记住步骤更加的有用。

二、Next Permutation

2.1 问题

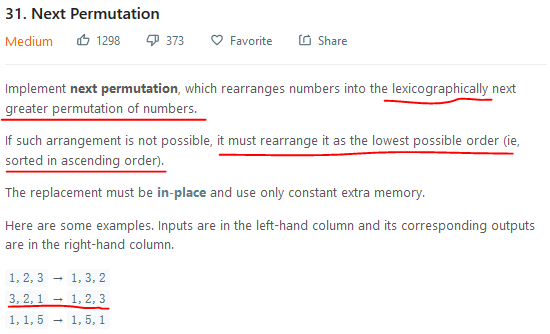
2.2 分析与解决

     排列（Arrangement），简单讲是从N个不同元素中取出M个，按照一定顺序排成一列，通常用A(M,N)表示。当M=N时，称为全排列（Permutation）。从数学角度讲，全排列的个数A(N,N)=(N)*(N-1)*...*2*1=N!，但从编程角度，如何获取所有排列？那么就必须按照某种顺序逐个获得下一个排列，通常按照升序顺序（字典序）获得下一个排列。
     例如对于一个集合A={1,2,3,}，首先获取全排列a1: 1,2,3,；然后获取下一个排列a2: 1,3,2,；按此顺序，A的全排列如下：

a1: 1,2,3;　　a2: 1,3,2;　　a3: 2,1,3;　　a4: 2,3,1;　　a5: 3,1,2;　　a6: 3,2,1;　　共6种。

    对于给定的任意一种全排列，如果能求出下一个全排列的情况，那么求得所有全排列情况就容易了。好在STL中的algorithm已经给出了一种健壮、高效的方法，下面进行介绍。

/**
 * current: 3   7  6  2  5  4  3  1  .
 *                    |  |     |     |
 *          find i----+  j     k     +----end
 * swap i and k :
 *          3   7  6  3  5  4  2  1  .
 *                    |  |     |     |
 *               i----+  j     k     +----end
 * reverse j to end :
 *          3   7  6  3  1  2  4  5  .
 *                    |  |     |     |
 *          find i----+  j     k     +----end
 * */

 具体方法为：
a）从后向前查找第一个相邻元素对(i,j)，并且满足A[i] < A[j]。易知，此时从j到end必然是降序。可以用反证法证明，请自行证明。
b）在[j,end)中寻找一个最小的k使其满足A[i]<A[k]。由于[j,end)是降序的，所以必然存在一个k满足上面条件；并且可以从后向前查找第一个满足A[i]<A[k]关系的k，此时的k必是待找的k。
c）将i与k交换。
    此时，i处变成比i大的最小元素，因为下一个全排列必须是与当前排列按照升序排序相邻的排列，故选择最小的元素替代i。易知，交换后的[j,end)仍然满足降序排序。因为在(k,end)中必然小于i，在[j,k)中必然大于k，并且大于i。
d）逆置[j,end)
     由于此时[j,end)是降序的，故将其逆置。最终获得下一全排序。
e) 结束
    如果在步骤a)找不到符合的相邻元素对，即此时i=begin，则说明当前[begin,end)为一个降序顺序，即无下一个全排列，STL的方法是将其逆置成升序。

    通过上面的描述，我们可以进行一次全排列的算法，就会发现真的非常的有用，那么到底是怎么相处这种方法呢？我想其中的有一点非常重要，那就是每次都要从最右边向左边找到两个相邻的元素，使得满足小于关系。然后将小于关系左边的数字与右边第一个大于左边的数字交换顺序，这样之后再将右边的序列按照从小到大顺序来排列，这样做的好处是使得算法能继续运行下去，最妙的是，将更大的数字交换到左边，随着循环顺序的加深肯定左边的数字会越来越大，最终直至变成从大到小顺序来排列，这样就达到了目的。

public class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while (i >= 0 && nums[i + 1] <= nums[i]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i + 1);
    }

    private void reverse(int[] nums, int start) {
        int i = start, j = nums.length - 1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

三、总结

    遇到有些问题，是大家共同的认识并且经过长期探索得到的，如果我们使用传统的方法可能需要花费非常多的时间，因此，我们平时要多做题，从而懂得更多。