乘风破浪:LeetCode真题_023_Merge k Sorted Lists
乘风破浪:LeetCode真题_023_Merge k Sorted Lists
一、前言
上次我们学过了合并两个链表,这次我们要合并N个链表要怎么做呢,最先想到的就是转换成2个链表合并的问题,然后解决,再优化一点的,就是两个两个合并,当然我们也可以一次性比较所有的元素,然后一点点的进行合并等等。
二、Merge k Sorted Lists
2.1 问题
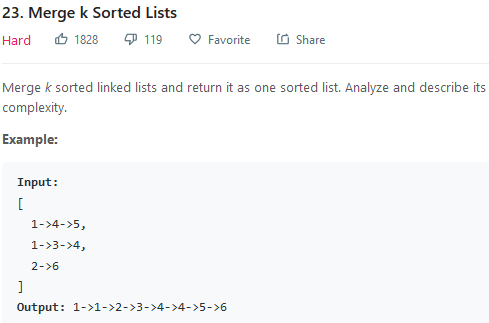
2.2 分析与解决
首先我们看看官方的解法:
第一种方法:暴力算法,将所有的元素放到一个数组里面,排序之后再用指针链接。
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
self.nodes = []
head = point = ListNode(0)
for l in lists:
while l:
self.nodes.append(l.val)
l = l.next
for x in sorted(self.nodes):
point.next = ListNode(x)
point = point.next
return head.next

第二种方法:用N个指针,每次比较最小的,然后连接起来。

第三种方法:通过优先级队列减少了一些比较的时间。
from Queue import PriorityQueue
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
head = point = ListNode(0)
q = PriorityQueue()
for l in lists:
if l:
q.put((l.val, l))
while not q.empty():
val, node = q.get()
point.next = ListNode(val)
point = point.next
node = node.next
if node:
q.put((node.val, node))
return head.next
第四种,我们提到过的转换成两个链表合并问题。

第五种,分治法合并,减少合并次数。
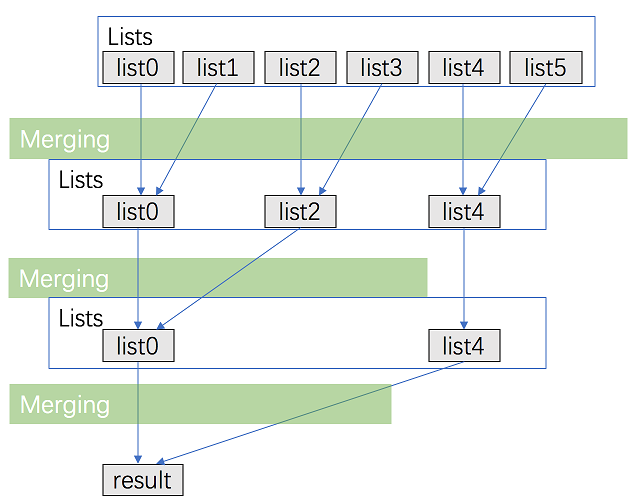
class Solution(object):
def mergeKLists(self, lists):
"""
:type lists: List[ListNode]
:rtype: ListNode
"""
amount = len(lists)
interval = 1
while interval < amount:
for i in range(0, amount - interval, interval * 2):
lists[i] = self.merge2Lists(lists[i], lists[i + interval])
interval *= 2
return lists[0] if amount > 0 else lists
def merge2Lists(self, l1, l2):
head = point = ListNode(0)
while l1 and l2:
if l1.val <= l2.val:
point.next = l1
l1 = l1.next
else:
point.next = l2
l2 = l1
l1 = point.next.next
point = point.next
if not l1:
point.next=l2
else:
point.next=l1
return head.next

我们的解法:其实和优先级队列很相似,都是使用了小根堆这样的结构来处理。
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
public class Solution {
/**
* <pre>
* Merge k sorted linked lists and return it as one sorted list.
* Analyze and describe its complexity.
*
* 题目大意:
* 合并k个排好的的单链表
*
* 解题思路:
* 使用一个小堆来进行操作,先将k个单链表的第一个结点入堆,再取堆中的最小素,此为最小的元素,
* 将这个元素的下一个结点堆,再取堆中最小的,依次操作直到堆为空
* </pre>
*
* @param lists
* @return
*/
public ListNode mergeKLists(ListNode[] lists) {
// 为空或者没有元素
if (lists == null || lists.length < 1) {
return null;
}
// 只有一个元素
if (lists.length == 1) {
return lists[0];
}
// 创建一个小顶堆,并且使用一个匿名内部类作为比较器
MinHeap<ListNode> minHeap = new MinHeap<ListNode>(new Comparator<ListNode>() {
@Override
public int compare(ListNode o1, ListNode o2) {
if (o1 == null) {
return -1;
}
if (o2 == null) {
return 1;
}
return o1.val - o2.val;
}
});
// 将数组中链表的第一个结点入堆
for (ListNode node : lists) {
if (node != null) {
minHeap.add(node);
}
}
// 头结点,作辅助使用
ListNode head = new ListNode(0);
// 当前处理的结点
ListNode curr = head;
while (!minHeap.isEmpty()) {
ListNode node = minHeap.deleteTop();
// 结点的下一个结点不为空就将下一个结点入堆
if (node.next != null) {
minHeap.add(node.next);
}
curr.next = node;
curr = node;
}
return head.next;
}
/**
* 小顶堆
*
* @param <T>
*/
private static class MinHeap<T> {
// 堆中元素存放的集合
private List<T> items;
private Comparator<T> comp;
/**
* 构造一个椎,始大小是32
*/
public MinHeap(Comparator<T> comp) {
this(32, comp);
}
/**
* 造诣一个指定初始大小的堆
*
* @param size 初始大小
*/
public MinHeap(int size, Comparator<T> comp) {
items = new ArrayList<>(size);
this.comp = comp;
}
/**
* 向上调整堆
*
* @param index 被上移元素的起始位置
*/
public void siftUp(int index) {
T intent = items.get(index); // 获取开始调整的元素对象
while (index > 0) { // 如果不是根元素
int parentIndex = (index - 1) / 2; // 找父元素对象的位置
T parent = items.get(parentIndex); // 获取父元素对象
if (comp.compare(intent, parent) < 0) { //上移的条件,子节点比父节点小
items.set(index, parent); // 将父节点向下放
index = parentIndex; // 记录父节点下放的位置
} else { // 子节点不比父节点小,说明父子路径已经按从小到大排好顺序了,不需要调整了
break;
}
}
// index此时记录是的最后一个被下放的父节点的位置(也可能是自身),
// 所以将最开始的调整的元素值放入index位置即可
items.set(index, intent);
}
/**
* 向下调整堆
*
* @param index 被下移的元素的起始位置
*/
public void siftDown(int index) {
T intent = items.get(index); // 获取开始调整的元素对象
int leftIndex = 2 * index + 1; // // 获取开始调整的元素对象的左子结点的元素位置
while (leftIndex < items.size()) { // 如果有左子结点
T minChild = items.get(leftIndex); // 取左子结点的元素对象,并且假定其为两个子结点中最小的
int minIndex = leftIndex; // 两个子节点中最小节点元素的位置,假定开始时为左子结点的位置
int rightIndex = leftIndex + 1; // 获取右子结点的位置
if (rightIndex < items.size()) { // 如果有右子结点
T rightChild = items.get(rightIndex); // 获取右子结点的元素对象
if (comp.compare(rightChild, minChild) < 0) { // 找出两个子节点中的最小子结点
minChild = rightChild;
minIndex = rightIndex;
}
}
// 如果最小子节点比父节点小,则需要向下调整
if (comp.compare(minChild, intent) < 0) {
items.set(index, minChild); // 将子节点向上移
index = minIndex; // 记录上移节点的位置
leftIndex = index * 2 + 1; // 找到上移节点的左子节点的位置
} else { // 最小子节点不比父节点小,说明父子路径已经按从小到大排好顺序了,不需要调整了
break;
}
}
// index此时记录是的最后一个被上移的子节点的位置(也可能是自身),
// 所以将最开始的调整的元素值放入index位置即可
items.set(index, intent);
}
/**
* 向堆中添加一个元素
*
* @param item 等待添加的元素
*/
public void add(T item) {
items.add(item); // 将元素添加到最后
siftUp(items.size() - 1); // 循环上移,以完成重构
}
/**
* 删除堆顶元素
*
* @return 堆顶部的元素
*/
public T deleteTop() {
if (items.isEmpty()) { // 如果堆已经为空,就报出异常
throw new RuntimeException("The heap is empty.");
}
T maxItem = items.get(0); // 获取堆顶元素
T lastItem = items.remove(items.size() - 1); // 删除最后一个元素
if (items.isEmpty()) { // 删除元素后,如果堆为空的情况,说明删除的元素也是堆顶元素
return lastItem;
}
items.set(0, lastItem); // 将删除的元素放入堆顶
siftDown(0); // 自上向下调整堆
return maxItem; // 返回堆顶元素
}
/**
* 判断堆是否为空
*
* @return true是空,false否
*/
public boolean isEmpty() {
return items.isEmpty();
}
}
}
三、总结
通过上面的分析我们可以发现只有不断的优化我们的算法,才能使得效率不断地提升,同时也锻炼了我们的思考能力。

