乘风破浪:LeetCode真题_014_Longest Common Prefix
乘风破浪:LeetCode真题_014_Longest Common Prefix
一、前言
如何输出最长的共同前缀呢,在给定的字符串中,我们可以通过笨办法去遍历,直到其中某一个字符不相等了,这样就得到了最长的前缀。那么还有没有别的办法呢?
二、Longest Common Prefix
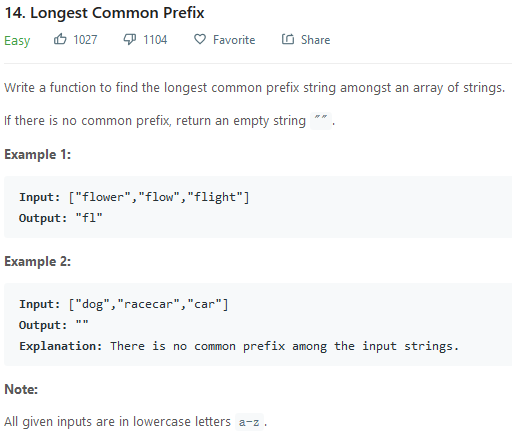
2.1 问题
2.2 分析与解决
由问题我们可以知道,所有的字符都是小写的,这样我们不需要纠结这一部分,其次就是如何设计一种算法来遍历了。我们可以先计算出字符串的最小长度,然后作为循环的次数 ,之后来对比和查看。当然我们还有其他的方法,比如横向的两个两个进行求集,最终得到结果,或者纵向的按照我们上面的方法去比较。或者用分治法,二分搜索法,甚至采用树状结构搜索法。
下面我们看看官网的答案:
横向搜索法:
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
String prefix = strs[0];
for (int i = 1; i < strs.length; i++)
while (strs[i].indexOf(prefix) != 0) {
prefix = prefix.substring(0, prefix.length() - 1);
if (prefix.isEmpty()) return "";
}
return prefix;
}
}
我们可以看到是非常巧妙的,通过第一个和第二个相比,刚开始使用indexOf()不成功会产生-1,如果成功了并且显示起始位置为0这样才算通过,其中每一次都是前缀去除一个字符来和原来的进行索引:prefix = prefix.substring(0, prefix.length() - 1);,然后将比较产生的prefix再和后面的继续比较,直至比较完毕得到想要的结果。
纵向搜索法:
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
for (int i = 0; i < strs[0].length() ; i++){
char c = strs[0].charAt(i);
for (int j = 1; j < strs.length; j ++) {
if (i == strs[j].length() || strs[j].charAt(i) != c)
return strs[0].substring(0, i);
}
}
return strs[0];
}
}
其实也是我们上面讲的,只不过没有比较最短长度而已。
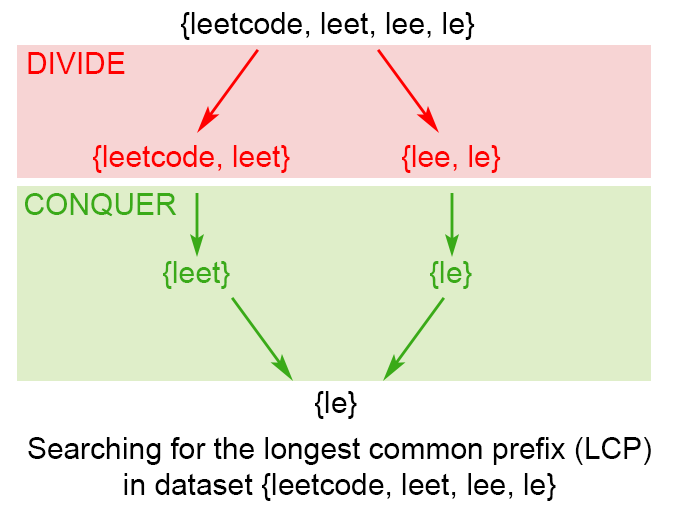
分治法,思路也很简单,两两合并加快合并的效率:
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
return longestCommonPrefix(strs, 0 , strs.length - 1);
}
private String longestCommonPrefix(String[] strs, int l, int r) {
if (l == r) {
return strs[l];
}
else {
int mid = (l + r)/2;
String lcpLeft = longestCommonPrefix(strs, l , mid);
String lcpRight = longestCommonPrefix(strs, mid + 1,r);
return commonPrefix(lcpLeft, lcpRight);
}
}
String commonPrefix(String left,String right) {
int min = Math.min(left.length(), right.length());
for (int i = 0; i < min; i++) {
if ( left.charAt(i) != right.charAt(i) )
return left.substring(0, i);
}
return left.substring(0, min);
}
}
相信看了代码和图片都能理解要表达的意思。
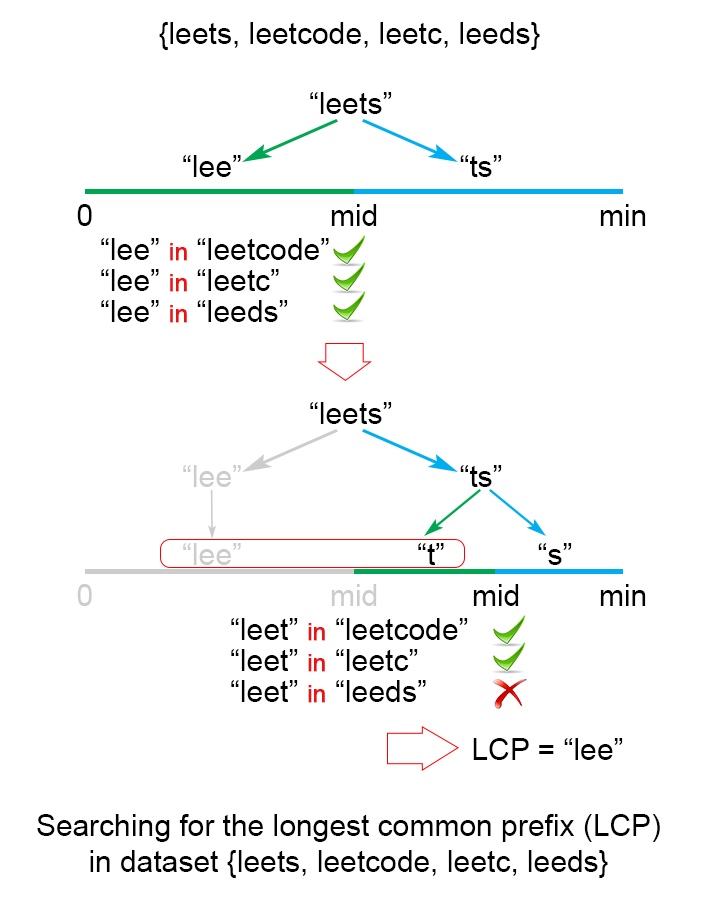
二分查找法:
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0)
return "";
int minLen = Integer.MAX_VALUE;
for (String str : strs)
minLen = Math.min(minLen, str.length());
int low = 1;
int high = minLen;
while (low <= high) {
int middle = (low + high) / 2;
if (isCommonPrefix(strs, middle))
low = middle + 1;
else
high = middle - 1;
}
return strs[0].substring(0, (low + high) / 2);
}
private boolean isCommonPrefix(String[] strs, int len){
String str1 = strs[0].substring(0,len);
for (int i = 1; i < strs.length; i++)
if (!strs[i].startsWith(str1))
return false;
return true;
}
}
通过找到最小的字符串长度,然后对所有的字符串按照这个长度进行二分查找,不断的细化下去,看看在细化的过程中是否有共同的前缀,最终返回结果。
我们的算法:
public class Solution {
/**
* 题目大意
* 写一个函数找出一个字串所数组中的最长的公共前缀。
*
* 解题思路
* 第一步先找出长度最小的字符串,然后将这个字符串与其它的字符串相比找出最短的最公共前缀。
*/
public String longestCommonPrefix(String[] strs) {
if (strs == null) {
return null;
}
if (strs.length == 0) {
return "";
}
int min = Integer.MAX_VALUE; // 记录最短的字符串的长度
// 找短字符串的长度
for (String str : strs) {
if (str == null) {
return null;
}
if (min > str.length()) {
min = str.length();
}
}
int i; // 记录最长前缀的字符数
boolean flag;
for (i = 0; i < min; i++) {
flag = true;
for (int j = 1; j < strs.length; j++) {
if (strs[0].charAt(i) != strs[j].charAt(i)) {
flag = false;
break;
}
}
if (!flag) {
break;
}
}
return strs[0].substring(0, i);
}
}
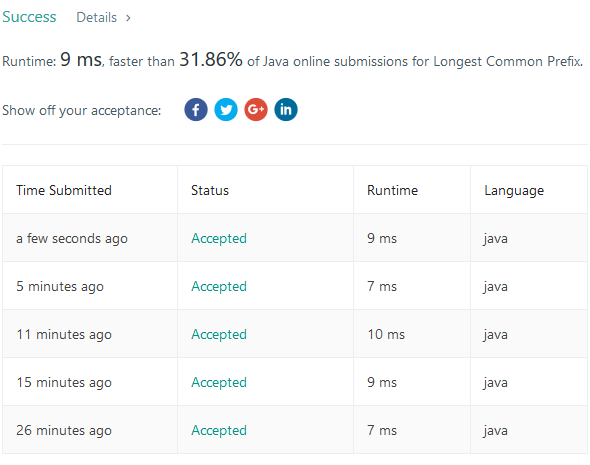
从下往上分别是上面几种算法的耗时情况,可以看到在这种情况下使用分治法和二分查找算法和其他算法基本上性能差不多。
三、总结
在这里我们更加明白了算法的意义和多样性,对于同一个问题从不同的角度思考就有不同的解答方式,这点是算法的迷人之处。


