乘风破浪:LeetCode真题_011_Container With Most Water
乘风破浪:LeetCode真题_011_Container With Most Water
一、前言
下面我们继续进行编程练习,可以说对于实际问题的活学活用是非常重要的。比如我们这次的题目,就需要从中找到问题的性质,然后去庖丁解牛。
二、Container With Most Water
2.1 问题理解

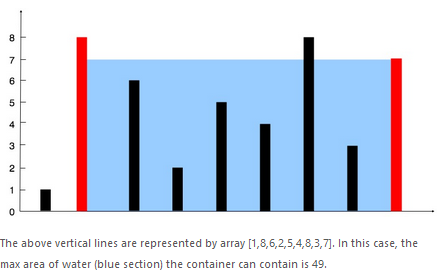
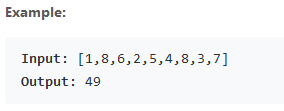
2.2 问题分析与解决
题意我们很容易读懂,就是求木桶的最大盛水量,底乘以高就可以了,其中底也非常容易求得,就是高需要取得两者的最小值。最简单的办法就是我们通过两个for循环,暴力的从开始遍历到结尾,这样选择最大的面积,但是会消耗很大的时间。因此,我们再想想能不能优化一下,我们可以想象有一种情况我们是会直接排除的,那就是如果我们最终选择了[i,j]区域内的面积最大,那么在i的左边肯定没有比a[i]更大的数据,并且在i的右边要选择数据的时候要选择大于a[i]的数据才可以;在j的右边也肯定没有比a[j]更大的数据,并且在j的左边要选择数据的时候要选择大于a[j]的数据才可以。于是我们定义两个指针i,j,从两端向中间收缩,收缩的顺序是先收缩min{a[i],a[j]}的指针,当我们收缩的时候,按照上面的要求,只有遇到了比自己更大的值才选择尝试计算面积,这样我们就能大大地节省时间,通过左右指针遍历到i==j的时候,将整个数组遍历一遍,程序结束。
让我们先看看官方的解答:
暴力算法:
public class Solution {
public int maxArea(int[] height) {
int maxarea = 0;
for (int i = 0; i < height.length; i++)
for (int j = i + 1; j < height.length; j++)
maxarea = Math.max(maxarea, Math.min(height[i], height[j]) * (j - i));
return maxarea;
}
}

优化算法:
public class Solution {
public int maxArea(int[] height) {
int maxarea = 0, l = 0, r = height.length - 1;
while (l < r) {
maxarea = Math.max(maxarea, Math.min(height[l], height[r]) * (r - l));
if (height[l] < height[r])
l++;
else
r--;
}
return maxarea;
}
}

注意:对于上面的算法,我们是否有疑惑的地方?我想是有的。如果仔细观察,我们会发现这样的做法会忽略当两个值相等时候的做法,无论是否正确都会简单地归给l++或者r--,这是非常不负责任的,假如本来的a[i+1]大于a[j-1],但是因为算法没有考虑到这一点,笼统的选择了r--,这样得到的结果(min{a[j-1],a[i]}*(j-1-i))肯定是小于(min{a[j],a[i+1]}*(j-1-i))的,因此可能会少比较一些这样的结果,导致最终的结果出现问题。所以官方的答案也只是参考答案,不一定完全正确的。关于这一点的评论,我们在下面会有提到,其实我们这种想法也是有局限性的,官方的还是有道理的。
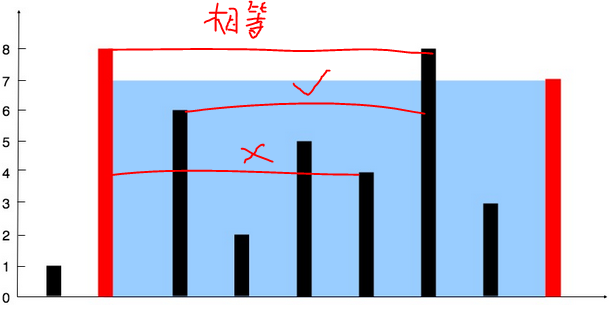
我们自己的解法:
public class Solution {
/**
*
* Note: You may not slant the container.
*
* 题目大意:
* 找两条竖线然后这两条线以及X轴构成的容器能容纳最多的水。
*
* 解题思路:
* 使用贪心算法,
* 1.首先假设我们找到能取最大容积的纵线为 i, j (假定i<j),
* 那么得到的最大容积 C = min( ai , aj ) * ( j- i) ;
*
* 2.下面我们看这么一条性质:
* ①: 在 j 的右端没有一条线会比它高!假设存在 k |( j<k && ak > aj) ,
* 那么 由 ak > aj,所以 min(ai, aj, ak) =min(ai, aj) ,
* 所以由i, k构成的容器的容积C' = min(ai, aj) * (k - i) > C,
* 与C是最值矛盾,所以得证j的后边不会有比它还高的线;
*
* ②:同理,在i的左边也不会有比它高的线;这说明什么呢?
* 如果我们目前得到的候选: 设为 x, y两条线(x< y),那么能够得到比
* 它更大容积的新的两条边必然在[x, y]区间内并且 ax' >= ax , ay' >= ay;
*
* 3.所以我们从两头向中间靠拢,同时更新候选值;在收缩区间的时候优先从
* x, y中较小的边开始收缩;
*/
public int maxArea(int[] height) {
// 参数校验
if (height == null || height.length < 2) {
return 0;
}
// 记录最大的结果
int result = 0;
// 左边的竖线
int left = 0;
// 右边的竖线
int right = height.length - 1;
while (left < right) {
// 设算当前的最大值
result = Math.max(result, Math.min(height[left], height[right]) * (right - left));
// 如果右边线高
if (height[left] < height[right]) {
int k = left;
// 从[left, right - 1]中,从左向右找,找第一个高度比height[left]高的位置
while (k < right && height[k] <= height[left]) {
k++;
}
// 从[left, right - 1]中,记录第一个比原来height[left]高的位置
left = k;
}
// 左边的线高
else if (height[left] > height[right]) {
int k = right;
// 从[left + 1, right]中,从右向左找,找第一个高度比height[right]高的位置
while (k > left && height[k] <= height[right]) {
k--;
}
// 从[left, right - 1]中,记录第一个比原来height[right]高的位置
right = k;
}else{
//当两个线一样高的时候,我们需要考虑相邻的两个值,哪个大选择哪个
if(left != right && height[left+1] < height[right-1]){
right-- ;
}else if(left != right && height[left+1] >= height[right-1]){
left++ ;
}
}
}
return result;
}
}

我们的算法其实是比官方更加优化的,因为我们少比较了一些本来不用比较的结果,但是因为在算法里面嵌套了一些循环,可能会误以为是O(n~2)的时间复杂度,其实仔细观察,我们从始至终只进行了一次遍历,里面的循环只是加速了遍历而已,因此时间复杂度还是O(n),从这里我们也知道不一定两个循环嵌套就是O(n~2)的复杂度。
补充说明:相信上面的向相等情况是大家最先想到并且不理解的,但是我上面提到的问题其实并不用解决,官方的答案还是有道理的,这是因为,从我上面画的图就可以看出来,最终无论选择哪一个,都没有原来的面积大,注定被舍弃。另外即使中间的两个都大于两边的,那也可以慢慢的等到这种情况出现,如果一个大,一个小,那么即使刚开始选择了小的,之后也会不断地选择,直到靠近大的。即使选择了大的,此时得到的面积也是小于原来的,除非下次小的不断增大,因此无论如何都没有隐患的。
三、总结
通过分析,我们可以发现,很多东西都是有一些细节在里面的,如果我们能够看到并且抓住这些东西就能将时间复杂度下降一个等级,并且也需要注意有些情况下是需要考虑相等的情况的,不能笼统的归向一边,除非经过仔细的考虑和斟酌。


