深度学习入门|第六章与学习相关的技巧（二）

与学习相关的技巧

前言

本文为本人学习深度学习入门一书的学习笔记，详情请阅读原著

四、正则化

机器学习的问题中，过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据，也希望模型可以进行正确的识别。我们可以制作复杂的、表现力强的模型，但是相应地，抑制过拟合的技巧也很重要。

1、过拟合

发生过拟合的原因，主要有以下两个

模型拥有大量参数、表现力强。
训练数据少

2、权值衰减

权值衰减是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大才发生的。

神经网络的学习目的是减小损失函数的值。这时，例如为损失函数加上权重的平方范数（L2 范数）。这样一来，就可以抑制权重变大。用符号表示的话，如果将权重记为 W，L2 范数的权值衰减就是 $\frac{1}{2}\lambda\boldsymbol{W}^2$ ，然后将这个 $\frac{1}{2}\lambda\boldsymbol{W}^2$ 加到损失函数上。这里，λ 是控制正则化强度的超参数。λ 设置得越大，对大的权重施加的惩罚就越重。此外， $\frac{1}{2}\lambda\boldsymbol{W}^2$ 开头的 $\frac{1}{2}$ 是用于将 $\frac{1}{2}\lambda\boldsymbol{W}^2$ 的求导结果变成 $\lambda\boldsymbol{W}$ 的调整用常量。

对于所有权重，权值衰减方法都会为损失函数加上 $\frac{1}{2}\lambda\boldsymbol{W}^2$ 。因此，在求权重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数 $\lambda\boldsymbol{W}$

L2 范数相当于各个元素的平方和。用数学式表示的话，假设有权重 W=(w1, w2,···,wn)，则 L2 范数可用 $\sqrt{w^2_1+w^2_2+\cdots+w^2_n}$ 计算出来。除了 L2 范数，还有 L1 范数、L ∞范数等。L1 范数是各个元素的绝对值之和，相当于 |w1| + |w2| +···+ |wn|。L∞范数也称为 Max 范数，相当于各个元素的绝对值中最大的那一个。L2 范数、L1 范数、L∞范数都可以用作正则化项，它们各有各的特点，不过这里我们要实现的是比较常用的 L2 范数。

3、Droupout

为损失函数加上权重的 L2 范数的权值衰减方法，该方法可以简单地实现，在某种程度上能够抑制过拟合。但是，如果网络的模型变得很复杂，只用权值衰减就难以应对了。在这种情况下，我们经常会使用 Dropout 方法。

Dropout 是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递，如图 6-22 所示。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。

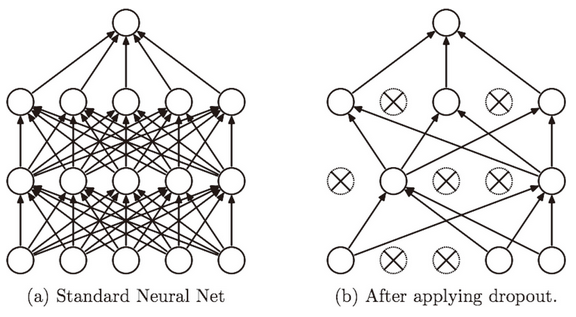
图 6-22　Dropout 的概念图：左边是一般的神经网络，右边是应用了 Dropout 的网络。Dropout 通过随机选择并删除神经元，停止向前传递信号

实现 Dropout。关于高效的实现，可以参考 Chainer 中实现的 Dropout。

class Dropout:
    def __init__(self, dropout_ratio=0.5):
        self.dropout_ratio = dropout_ratio
        self.mask = None

    def forward(self, x, train_flg=True):
        if train_flg:
            self.mask = np.random.rand(*x.shape) > self.dropout_ratio
            return x * self.mask
        else:
            return x * (1.0 - self.dropout_ratio)

    def backward(self, dout):
        return dout * self.mask

要点：每次正向传播时，self.mask 中都会以 False 的形式保存要删除的神经元。self.mask 会随机生成和 x 形状相同的数组，并将值比dropout_ratio 大的元素设为 True。反向传播时的行为和 ReLU 相同。也就是说，正向传播时传递了信号的神经元，反向传播时按原样传递信号；正向传播时没有传递信号的神经元，反向传播时信号将停在那里。

机器学习中经常使用集成学习。所谓集成学习，就是让多个模型单独进行学习，推理时再取多个模型的输出的平均值。用神经网络的语境来说，比如，准备 5 个结构相同（或者类似）的网络，分别进行学习，测试时，以这 5 个网络的输出的平均值作为答案。实验告诉我们，通过进行集成学习，神经网络的识别精度可以提高好几个百分点。这个集成学习与 Dropout 有密切的关系。这是因为可以将 Dropout 理解为，通过在学习过程中随机删除神经元，从而每一次都让不同的模型进行学习。并且，推理时，通过对神经元的输出乘以删除比例（比如，0.5 等），可以取得模型的平均值。也就是说，可以理解成，Dropout将集成学习的效果（模拟地）通过一个网络实现了。

五、超参数的验证

神经网络中，除了权重和偏置等参数，超参数（hyper-parameter）也经常出现。这里所说的超参数是指，比如各层的神经元数量、batch 大小、参数更新时的学习率或权值衰减等。

1、验证数据

将数据集分成了训练数据和测试数据，训练数据用于学习，测试数据用于评估泛化能力。

注意：不能使用测试数据评估超参数的性能。因为如果使用测试数据调整超参数，超参数的值会对测试数据发生过拟合。换句话说，用测试数据确认超参数的值的“好坏”，就会导致超参数的值被调整为只拟合测试数据。这样的话，可能就会得到不能拟合其他数据、泛化能力低的模型。

因此，调整超参数时，必须使用超参数专用的确认数据。用于调整超参数的数据，一般称为验证数据（validation data）。我们使用这个验证数据来评估超参数的好坏。

训练数据用于参数（权重和偏置）的学习，验证数据用于超参数的性能评估。为了确认泛化能力，要在最后使用（比较理想的是只用一次）测试数据。

2、超参数的最优化

进行超参数的最优化时，逐渐缩小超参数的“好值”的存在范围非常重要。所谓逐渐缩小范围，是指一开始先大致设定一个范围，从这个范围中随机选出一个超参数（采样），用这个采样到的值进行识别精度的评估；然后，多次重复该操作，观察识别精度的结果，根据这个结果缩小超参数的“好值”的范围。通过重复这一操作，就可以逐渐确定超参数的合适范围。

在进行神经网络的超参数的最优化时，与网格搜索等有规律的搜索相比，随机采样的搜索方式效果更好。这是因为在多个超参数中，各个超参数对最终的识别精度的影响程度不同。

超参数的范围只要“大致地指定”就可以了。所谓“大致地指定”，是指像 0.001（10-3）到 1000（103）这样，以“10 的阶乘”的尺度指定范围（也表述为“用对数尺度（log scale）指定”）。

在超参数的搜索中，需要尽早放弃那些不符合逻辑的超参数。于是，在超参数的最优化中，减少学习的 epoch，缩短一次评估所需的时间是一个不错的办法。

以上就是超参数的最优化的内容，简单归纳一下，如下所示。

步骤 0

设定超参数的范围。

步骤 1

从设定的超参数范围中随机采样。

步骤 2

使用步骤 1 中采样到的超参数的值进行学习，通过验证数据评估识别精度（但是要将 epoch 设置得很小）。

步骤 3

重复步骤 1 和步骤 2（100 次等），根据它们的识别精度的结果，缩小超参数的范围。

反复进行上述操作，不断缩小超参数的范围，在缩小到一定程度时，从该范围中选出一个超参数的值。这就是进行超参数的最优化的一种方法。

这里介绍的超参数的最优化方法是实践性的方法。不过，这个方法与其说是科学方法，倒不如说有些实践者的经验的感觉。在超参数的最优化中，如果需要更精炼的方法，可以使用贝叶斯最优化（Bayesian optimization）。贝叶斯最优化运用以贝叶斯定理为中心的数学理论，能够更加严密、高效地进行最优化。详细内容请参考论文“Practical Bayesian Optimization of Machine Learning Algorithms” 等。

posted @ 2019-05-12 18:55 砍柴人Ryan 阅读(498) 评论(0) 编辑收藏举报

刷新页面返回顶部

砍-柴-人