深度学习入门|第五章 误差反向传播法
误差反向传播法
前言
此为本人学习《深度学习入门》的学习笔记,详情请阅读原书
数值微分虽然简单,也容易实现,但是缺点是计算上比较费时间,本章介绍一个高效计算权重参数的梯度的方法--误差反向传播法
一、计算图
计算图将计算过程用图形表示出来。这里说的图形是数据结构图,通过多个节点和边表示(连接节点的直线称为“边”)。
1、用计算图求解
实例:太郎在超市买了 2 个苹果、3 个橘子。其中,苹果每个 100 日元,橘子每个 150 日元。消费税是 10%,请计算支付金额。
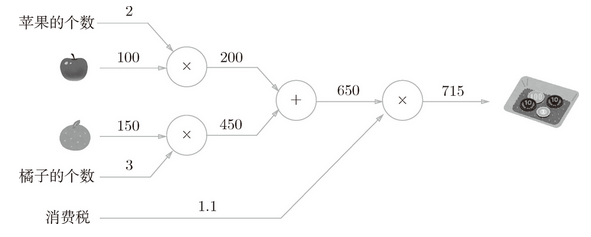
图 5-3 基于计算图求解的答案
用计算图解题的情况下,需要按如下流程进行。
- 构建计算图。
- 在计算图上,从左向右进行计算。
这里的第 2 歩“从左向右进行计算”是一种正方向上的传播,简称为正向传播(forward propagation)。正向传播是从计算图出发点到结束点的传播。考虑反向(从图上看的话,就是从右向左)的传播。实际上,这种传播称为反向传播(backward propagation)。反向传播将在接下来的导数计算中发挥重要作用。
2、局部计算
计算图的特征是可以通过传递“局部计算”获得最终结果。“局部”这个词的意思是“与自己相关的某个小范围”。局部计算是指,无论全局发生了什么,都能只根据与自己相关的信息输出接下来的结果。
计算图可以集中精力于局部计算。无论全局的计算有多么复杂,各个步骤所要做的就是对象节点的局部计算。虽然局部计算非常简单,但是通过传递它的计算结果,可以获得全局的复杂计算的结果。
3、为何用计算图的解题
优点:1、局部计算,无论全局多么复杂,都可以通过局部计算使各个节点致力于简单计算,从而简化问题
2、利用计算图可以将中间的计算结果全部保存起来
3、可以通过反向传播高效计算导数(最大优点)

图 5-5 基于反向传播的导数的传递
如图 5-5 所示,反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1 → 1.1 → 2.2)。
二、链式法则
1、计算图的反向传播
从实例出发
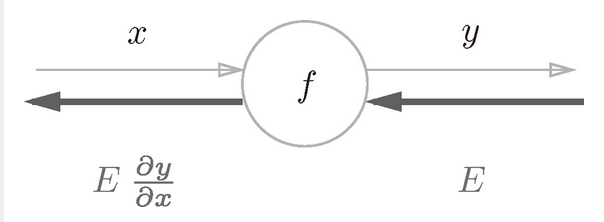
图 5-6 计算图的反向传播:沿着与正方向相反的方向,乘上局部导数
如图,反向传播的计算顺序是,将信号E乘以结点的局部导数 ,然后将结果传递给下一个结点。这里所说的局部导数是指正向传播中y=f(x)的导数,也就是y关于x的导数
。比如,假设 y=f(x)=x2,则局部导数为
。把这个局部导数乘以上游传过来的值(本例中为 E),然后传递给前面的节点。
这就是反向传播的计算顺序。通过这样的计算,可以高效的求出导数的值,这是反向传播的要点。
2、什么是链式法则
介绍链式法则时,需要先从复合函数说起。比如,z=(x+y)2 是由式(5.1)所示的两个式子构成的。
z = t2
t = x + y (5.1)
链式法则时关于复合函数的导数的性质,定义如下
如果某各个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示
以式(5.1)为例,(z 关于 x 的导数)可以用
(z 关于 t 的导数)和
(t 关于 x 的导数)的乘积表示。用数学式表示的话,可以写成式(5.2)。
![]()
式(5.2)中的 可以互相抵消
![]()
使用链式法则实例:使用式子(5.2)的导数。为此先求式子(5.1)中的局部导数(偏导数)

如式(5.3), 等于 2t,
等于 1。这是基于导数公式的解析解。然后,最后要计算的
可由式(5.3)求得的导数的乘积计算出来。
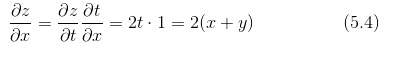
3、链式法则和计算图
尝试将式(5.4)的链式法则的计算用计算图表示出来。如果用“**2”节点表示平方运算的话,则计算图如图 5-7 所示。
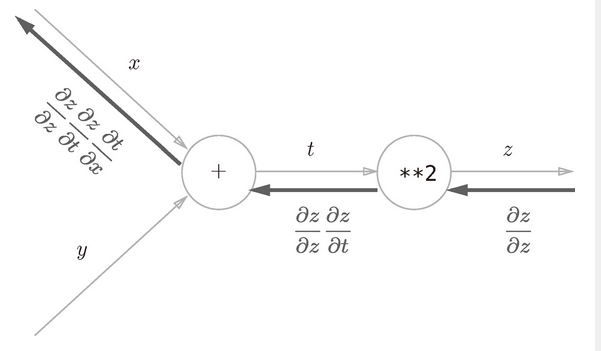
图 5-7 式(5.4)的计算图:沿着与正方向相反的方向,乘上局部导数后传递
如图所示,计算图的反向传播从右到左传播信号。反向传播的计算顺序是,先将节点的输入信号乘以节点的局部导数(偏导数),然后再传递给下一个节点。比如,反向传播时,“**2”节点的输入是 ,将其乘以局部导数
(因为正向传播时输入是 t、输出是 z,所以这个节点的局部导数是
),然后传递给下一个节点。另外,图 5-7 中反向传播最开始的信号
在前面的数学式中没有出现,这是因为
,所以在刚才的式子中被省略了。
图 5-7 中需要注意的是最左边的反向传播的结果。根据链式法则, 成立,对应“z 关于 x 的导数”。也就是说,反向传播是基于链式法则的。
把式(5.3)的结果代入到图 5-7 中,结果如图 5-8 所示, 的结果为 2(x + y)。
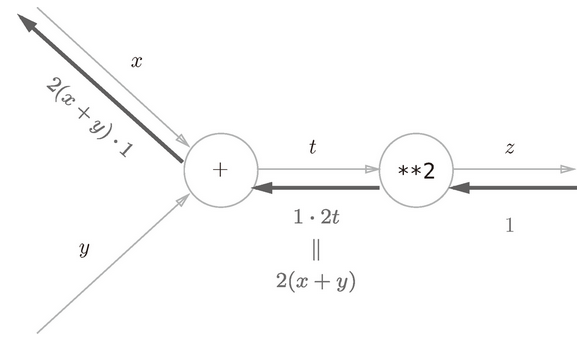
图 5-8 根据计算图的反向传播的结果, 等于 2(x + y)
三、反向传播
本节将以“+”和“×”等运算为例,介绍反向传播的结构。
1、加法结点的反向传播
以 z = x + y 为对象,观察它的反向传播。z= x + y 的导数可由下式(解析性地)计算出来。

如式(5.5)所示, 和
同时都等于 1。因此,用计算图表示的话,如图 5-9 所示。
在图 5-9 中,反向传播将从上游传过来的导数(本例中是 )乘以 1,然后传向下游。也就是说,因为加法节点的反向传播只乘以 1,所以输入的值会原封不动地流向下一个节点。
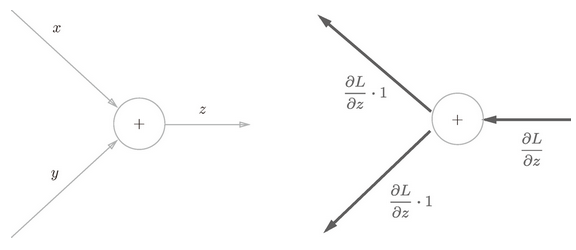
图 5-9 加法节点的反向传播:左图是正向传播,右图是反向传播。如右图的反向传播所示,加法节点的反向传播将上游的值原封不动地输出到下游
2、乘法结点的反向传播
考虑 z = xy。这个式子的导数用式(5.6)表示。

根据式(5.6),可以像图 5-12 那样画计算图。
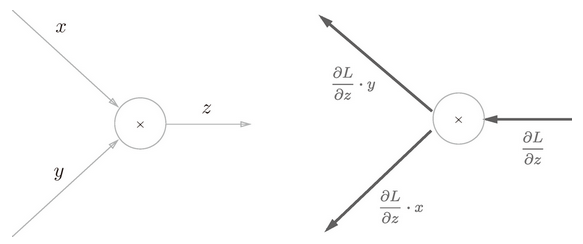
图 5-12 乘法的反向传播:左图是正向传播,右图是反向传播
乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系,如图 5-12 所示,正向传播时信号是 x 的话,反向传播时则是 y;正向传播时信号是 y 的话,反向传播时则是 x。
具体的例子。比如,假设有“10 × 5 = 50”这一计算,反向传播时,从上游会传来值 1.3。用计算图表示的话,如图 5-13 所示。
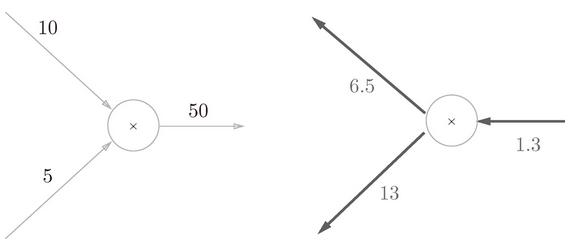
图 5-13 乘法节点的反向传播的具体例子




