深度学习入门|第四章 神经网络的学习（二）

第四章 神经网络的学习

前言

此为本人学习《深度学习入门》的学习笔记

三、数值微分

梯度法使用梯度的信息决定前进的方向

1、导数

\frac{df(x)}{dx}=\lim_{h\to0} \frac{f(x+h)-f(x)}{h} 　　　　(4.4)

式（4.4）表示的是函数的导数。左边的符号 \frac{{\rm d}f(x)}{{\rm d}x} 表示 f（x）关于 x 的导数，即f（x）相对于 x 的变化程度。式（4.4）表示的导数的含义是，x 的“微小变化”将导致函数 f（x）的值在多大程度上发生变化。其中，表示微小变化的 h 无限趋近 0，表示为 \lim_{h\to0}。

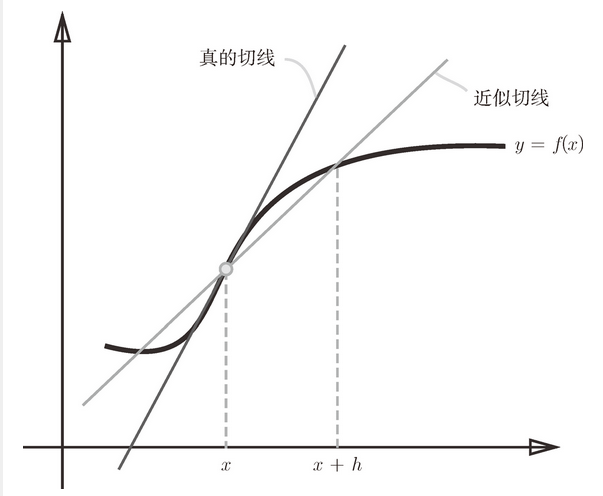
图 4-5　真的导数（真的切线）和数值微分（近似切线）的值不同

def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

如上所示，利用微小的差分求导数的过程称为数值微分（numerical differentiation）。而基于数学式的推导求导数的过程，则用“解析性”（analytic）一词，称为“解析性求解”或者“解析性求导”。比如，y = x2的导数，可以通过 \frac{{\rm d} y}{{\rm d} x}=2x 解析性地求解出来。因此，当 x = 2 时，y 的导数为 4。解析性求导得到的导数是不含误差的“真的导数”。

2、数值微分的例子

用上述的数值微分对简单函数进行求导,以y=0.01x2+0.1x为例。

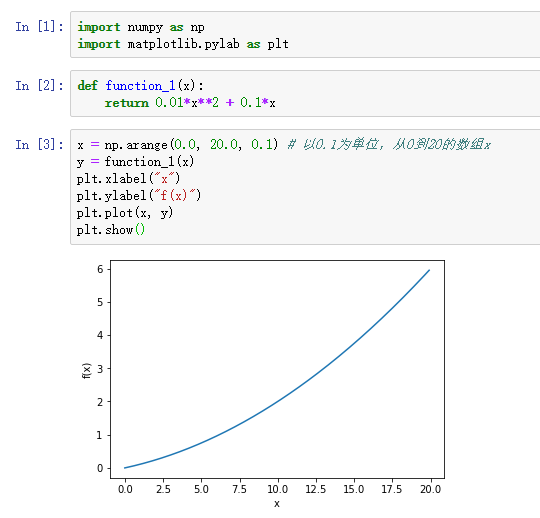
计算该函数在x=5和x=10处的导数

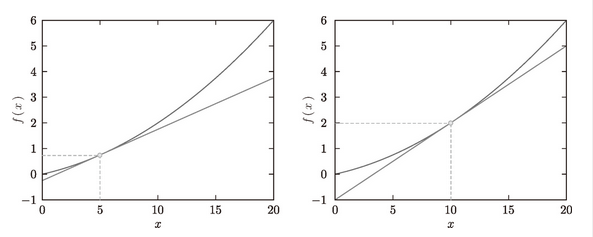
图 4-7　x=5、x=10处的切线：直线的斜率使用数值微分的值

3、偏导数

如函数表达式f(x_{0},x_{1} )=x_{0}^2+x_{1}^2 ,，有两个变量

用python实现

def function_2(x):
return x[0]**2 + x[1]**2
# 或者return np.sum(x**2)

函数图像

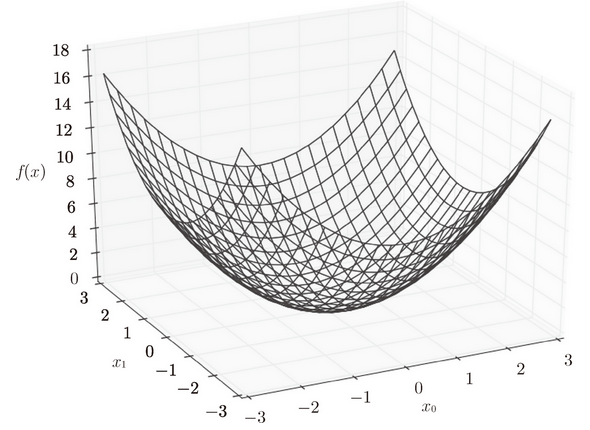
图 4-8 f(x_{0},x_{1} )=x_{0}^2+x_{1}^2 的图像

把这里讨论的有多个变量的函数的导数称为偏导数。用数学式表示的话，可以写成 \frac{\partial f}{\partial x_0}、\frac{\partial f}{\partial x_1}。

问题 1：求 x0=3，x1=4时，关于 x_0 的偏导数 \frac{\partial f}{\partial x_0}。

>>> def function_tmp1(x0):
...     return x0*x0 + 4.0**2.0
...
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378

问题 2：求 x0=3，x1=4 时，关于 x_1 的偏导数 \frac{\partial f}{\partial x_1}。

>>> def function_tmp2(x1):
...     return 3.0**2.0 + x1*x1
...
>>> numerical_diff(function_tmp2, 4.0)
7.999999999999119

偏导数和单变量的导数一样，都是求某个地方的斜率。不过，偏导数需要将多个变量中的某一个变量定为目标变量，并将其他变量固定为某个值。

四、梯度

像 \Bigl(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}\Bigr) 这样的由全部变量的偏导数汇总而成的向量称为梯度（gradient）。梯度可以像下面这样来实现。

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) # 生成和x形状相同的数组

    for idx in range(x.size):
        tmp_val = x[idx]
        # f(x+h)的计算
        x[idx] = tmp_val + h
        fxh1 = f(x)

        # f(x-h)的计算
        x[idx] = tmp_val - h
        fxh2 = f(x)

        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 还原值

    return grad

求点 (3, 4)、(0, 2)、(3, 0) 处的梯度

1.梯度法

机器学习的主要任务是在学习时寻找最优参数。同样地，神经网络也必须在学习时找到最优参数（权重和偏置）。这里所说的最优参数是指损失函数取最小值时的参数。一般而言，损失函数很复杂，参数空间庞大，我们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值（或者尽可能小的值）的方法就是梯度法。

注意：梯度表示的是各点处的函数值减小最多的方向。

函数的极小值、最小值以及被称为鞍点（saddle point）的地方，梯度为 0。极小值是局部最小值，也就是限定在某个范围内的最小值。鞍点是从某个方向上看是极大值，从另一个方向上看则是极小值的点。虽然梯度法是要寻找梯度为 0 的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点）。此外，当函数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区，陷入被称为“学习高原”的无法前进的停滞期。

通过不断地沿梯度方向前进，逐渐减小函数值的过程就是梯度法（gradient method）。梯度法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。

用数学式来表示梯度法，如式（4.7）所示

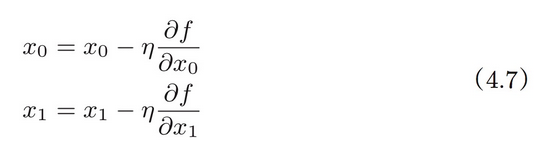
式（4.7）的 η 表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。

用 Python 来实现梯度下降法

def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x

    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x

参数 f 是要进行最优化的函数，init_x 是初始值，lr 是学习率 learning rate，step_num 是梯度法的重复次数。numerical_gradient(f,x) 会求函数的梯度，用该梯度乘以学习率得到的值进行更新操作，由 step_num 指定重复的次数。

 实例;用梯度法求 f(x_0+x_1)=x^2_0+x^2_1 的最小值。

设初始值为 (-3.0, 4.0)，开始使用梯度法寻找最小值。最终的结果是(-6.1e-10, 8.1e-10)，非常接近 (0, 0)。实际上，真的最小值就是 (0, 0)，所以说通过梯度法我们基本得到了正确结果。

注意：学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。也就是说，设定合适的学习率是一个很重要的问题。

像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。

2. 神经网络的梯度

神经网络的学习也要求梯度。这里所说的梯度是指损失函数关于权重参数的梯度。比如，有一个只有一个形状为 2 × 3 的权重 W 的神经网络，损失函数用 L 表示。此时，梯度可以用 \frac{\partial L}{\partial \boldsymbol{W}} 表示。用数学式表示的话，如下所示

\frac{\partial L}{\partial \boldsymbol{W}} 的元素由各个元素关于 W 的偏导数构成。比如，第 1 行第 1 列的元素 \frac{\partial L}{\partial w_{11}} 表示当 w_{11}  稍微变化时，损失函数 L 会发生多大变化。这里的重点是，\frac{\partial L}{\partial \boldsymbol{W}} 的形状和 W 相同。实际上，式（4.8）中的 W 和 \frac{\partial L}{\partial \boldsymbol{W}} 都是 2 × 3 的形状。

五、学习算法的实现

前提

神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面 4 个步骤。

步骤 1（mini-batch）

从训练数据中随机选出一部分数据，这部分数据称为 mini-batch。我们的目标是减小 mini-batch 的损失函数的值。

步骤 2（计算梯度）

为了减小 mini-batch 的损失函数的值，需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。

步骤 3（更新参数）

将权重参数沿梯度方向进行微小更新。

步骤 4（重复）

重复步骤 1、步骤 2、步骤 3。

 

posted @ 2019-05-12 18:53  砍柴人Ryan  阅读(544)  评论(0)  编辑  收藏  举报