洛谷 P1038 :神经网络(BFS && 拓扑排序)
题目背景
人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向,兰兰同学在自学了一本神经网络的入门书籍后,提出了一个简化模型,他希望你能帮助他用程序检验这个神经网络模型的实用性。
题目描述
在兰兰的模型中,神经网络就是一张有向图,图中的节点称为神经元,而且两个神经元之间至多有一条边相连,下图是一个神经元的例子:
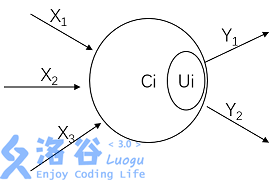
神经元〔编号为1)
图中,X1−X3是信息输入渠道,Y1−Y2是信息输出渠道,C1表示神经元目前的状态,Ui是阈值,可视为神经元的一个内在参数。
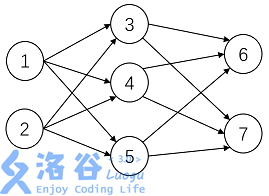
神经元按一定的顺序排列,构成整个神经网络。在兰兰的模型之中,神经网络中的神经元分为几层;称为输入层、输出层,和若干个中间层。每层神经元只向下一层的神经元输出信息,只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。
兰兰规定,Ci服从公式:(其中n是网络中所有神经元的数目)
![]()
公式中的Wji(可能为负值)表示连接j号神经元和i号神经元的边的权值。当 Ci大于0时,该神经元处于兴奋状态,否则就处于平静状态。当神经元处于兴奋状态时,下一秒它会向其他神经元传送信号,信号的强度为Ci。
如此.在输入层神经元被激发之后,整个网络系统就在信息传输的推动下进行运作。现在,给定一个神经网络,及当前输入层神经元的状态(Ci),要求你的程序运算出最后网络输出层的状态。
输入格式
输入文件第一行是两个整数n(1≤n≤100)和p。接下来n行,每行2个整数,第i+1行是神经元iii最初状态和其阈值(Ui),非输入层的神经元开始时状态必然为0。再下面P行,每行由2个整数i,j及1个整数Wij,表示连接神经元i,j的边权值为Wij。
输出格式
输出文件包含若干行,每行有2个整数,分别对应一个神经元的编号,及其最后的状态,2个整数间以空格分隔。仅输出最后状态大于0的输出层神经元状态,并且按照编号由小到大顺序输出。
若输出层的神经元最后状态均为 0,则输出 “NULL”。
输入输出样例
输入 #1
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1
输出 #1
3 1
4 1
5 1解题思路:
相当于一个拓扑排序, 但是初始可以判断一下c[i]!=0时就是入度为0的点, 然后把入度为0的点入队,在BFS遍历所有相邻的点,更新c[i]的值即可, u[i]是可以在最开始的时候就减去,对答案没有影响.
#include <bits/stdc++.h>
const int N = 120;
using namespace std;
int n, p;
int e[N][N], out[N], c[N], u[N];
bool book[N];
void init()
{
memset(book, false, sizeof(book));
memset(e, 0, sizeof(e));
memset(out, 0, sizeof(out));
}
int main()
{
queue<int>q;
int a, b, w;
while(scanf("%d%d", &n, &p)!=EOF)
{
init();
for(int i=1; i<=n; i++) {
scanf("%d%d", &c[i], &u[i]);
if(c[i]!=0) {
q.push(i);
book[i] = true;
}
else c[i]-=u[i];
}
for(int i=0; i<p; i++) {
scanf("%d%d%d", &a, &b, &w);
e[a][b] = w;
out[a]++;
}
while(!q.empty()) {
int u = q.front();
q.pop();
if(c[u] > 0) {
for(int i=1; i<=n; i++)
if(e[u][i] != 0) {
c[i]+=e[u][i]*c[u];
if(book[i] == false) {
q.push(i);
book[i] = true;
}
}
}
}
int temp=0;
for(int i=1; i<=n; i++) {
if(out[i] == 0 && c[i] > 0)
{
temp=1;
break;
}
}
if(temp==0)
printf("NULL\n");
else {
for(int i=1; i<=n; i++)
if(out[i] == 0 && c[i] > 0)
printf("%d %d\n", i, c[i]);
}
}
return 0;
}


