详解逆波兰表达式的转换与求值
对于计算一个算式 如 : 3*(5+6)-2
这种算式叫做中缀表达式, 人们看着会比较方便, 如果用计算机直接计算会很麻烦,所以要把中缀表达式变为计算机易于理解的后缀表达式来计算.
后缀表达式又叫逆波兰表达式, 把运算量写在前面, 把运算符写在后面, 并且可以去掉括号
如 a+b 变为 a b +
a*(b+c) 可以变为 a b c + *
将普通算式转化为逆波兰表达式的步骤如下:
1. 从左到右扫描算式, 如果是数字, 计算数字的值后直接输出
2. 如果是左括号, 直接加入栈
3. 如果是右括号,查询栈顶是否为左括号, 如果是, 把左括号出栈,
如果不是,输出栈顶的符号, 出栈, 继续第三步, 直到找到左括号
4. 如果是 +, -, *, /, 运算符,比较当前运算符和栈顶运算符的优先级,
如果该运算符的优先级大于栈顶运算符的优先级或者栈为空或者栈顶符号为括号, 把该运算符入栈,
否则, 也就是小于等于的情况, 输出栈顶的符号, 出栈.
将算式中的所有元素都处理完后即可得到该算式逆波兰表达式.
C++代码如下:
#include <bits/stdc++.h>
using namespace std;
char str[100][20];
int len=0; //记录输入的算式长度
/*
*用于计算运算符的优先级
*/
int Grade(char ch)
{
if(ch=='*' || ch=='/')
return 2;
else if(ch=='+' || ch=='-')
return 1;
else return 0;
}
void Against()
{
stack<char>s;
//输出原算式
printf("原算式:\n");
for(int i=0 ;i<len; i++)
printf("%s ", str[i]);
printf("\n");
printf("转化成逆波兰表达式:\n");
//转化成逆波兰表达式
for(int i=0; i<len; i++) {
//如果是数直接输出这个数
if(str[i][0]>='0' && str[i][0]<='9')
printf("%s ", str[i]);
//不是数,就为运算符,这是在输入的中缀式合法的情况下计算的
else if(s.empty()) {
//当栈为空时,直接把当前运算符入栈
s.push(str[i][0]);
}
//当运算符为左括号时,无条件入栈
else if(str[i][0]=='(')
s.push('(');
else if(str[i][0]==')') {
/*
*当运算符为有括号时, 查看栈顶元素,
*当栈顶元素不为左括号,出栈并输出
*当栈顶元素为左括号时,出栈
*/
while(1) {
char ch = s.top();
if(ch!='(') {
s.pop();
printf("%c ", ch);
}
else {
s.pop();
break;
}
}
}
else {
/*判断 +, -, *, /, 四种符号*/
while(1) {
//如果栈为空, 入栈
if(s.empty()) {
s.push(str[i][0]);
break;
}
/*
*比较当前运算符和栈顶运算符的优先级
*如果当前的大于栈顶的,入栈
*否则出栈输出并继续比较
*/
char ch = s.top();
char operater = str[i][0];
if(Grade(operater) > Grade(ch)){
//((operater == '*' || operater=='/') && (ch=='+' || ch=='-') || ch=='(')
//两种if条件都可以判断运算符的优先级
s.push(operater);
break;
}
else {
s.pop();
printf("%c ", ch);
}
}
}
}
//把剩下栈中的运算符输出
while(!s.empty())
{
printf("%c ", s.top());
s.pop();
}
}
int main()
{
/*
*输入时注意每个数和运算符要分开,为了以后比较好判断
*/
while(scanf("%s", str[len++])!=EOF);
len--;
Against();
}
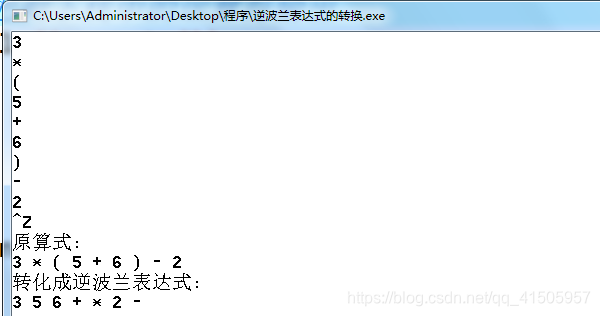
以 3*(5+6)-2 为例, 转化成逆波兰表达式为 3 5 6 + * 2 -
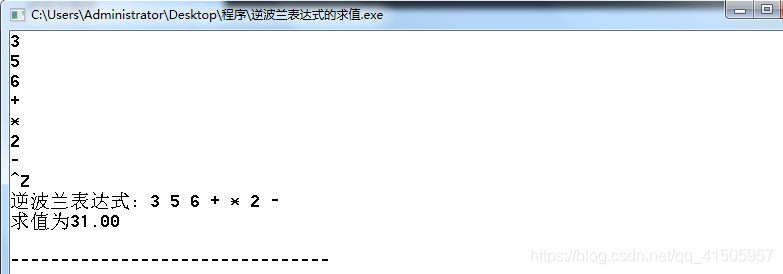
那么逆波兰表达式该如何计算?
逆波兰表达式的计算机比较简单了.
给出一个逆波兰表达式, 计算过程如下:
1. 判断是数字还是运算符, 如果是数字, 求出数字的值后入栈.
2. 如果是运算符,从栈中出栈两个数字, 用后出栈的数与前出栈的数根据运算符运算, 再把得到的值入栈.
可能这句话不太好理解, 如过先出栈的为num1, 后出栈的是num2, 运算符为减号时, 新的数 num3 = num2 - num1.
C++代码如下
#include <bits/stdc++.h>
using namespace std;
char str[100][20];
int len=0; //记录输入的算式长度
int Value_Against()
{
stack<double>s;
printf("逆波兰表达式: ");
for(int i=0; i<len; i++)
printf("%s ", str[i]);
printf("\n");
//遍历每个字符串
for(int i=0; i<len; i++) {
//如果为数字,计算出数字,入栈
if(str[i][0] >= '0' && str[i][0] <= '9') {
int num=0;
for(int j=0; j<strlen(str[i]); j++)
num = num*10 + (str[i][j] - '0');
s.push(num);
}
else {
/*
*如果是运算符,从栈中弹出两个数,
*根据运算符计算后把新的数入栈
*/
double num1 = s.top();
s.pop();
double num2 = s.top();
s.pop();
double num3;
if(str[i][0] == '+')
num3 = num2 + num1;
else if(str[i][0] == '-')
num3 = num2 - num1;
else if(str[i][0] == '*')
num3 = num2 * num1;
else if(str[i][0] == '/')
num3 = num2 / num1;
s.push(num3);
}
}
//最后栈顶元素即为答案
printf("求值为%.2lf\n", s.top());
}
int main()
{
while(scanf("%s", str[len++])!=EOF);
len--;
Value_Against();
} 就以上面已经转化好的逆波兰表达式为例
可以求出 3*(5+6)-2 的值为 31