hihoCoder1151: 骨牌覆盖问题·二
http://hihocoder.com/problemset/problem/1151
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
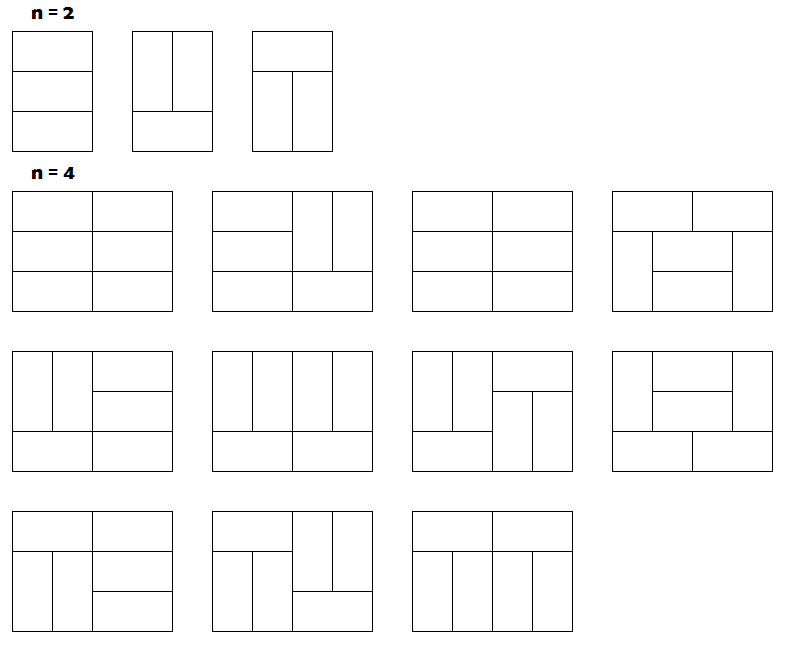
上一周我们研究了2xN的骨牌问题,这一周我们不妨加大一下难度,研究一下3xN的骨牌问题?
所以我们的题目是:对于3xN的棋盘,使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢?
首先我们可以肯定,奇数长度一定是没有办法覆盖的;对于偶数长度,比如2,4,我们有下面几种覆盖方式:
输入
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
输出
第1行:1个整数,表示覆盖方案数 MOD 12357
样例输入
62247088样例输出
4037提示上没看懂,自己推出来的公式f[n]=3*f[n-2]+2*f[n-4]+2*f[n-6]+…….+2*f[0];开1亿的数组内存超了,只能这样写了。
公式第一个3*f[n-2]比较好推,在原有的基础上加上2*3的棋盘有3种排列,前面的有f[n-2]种,在增加后两个2*3之间连接处可以有两种可能,就是在上图n=4的第二行和第三行最后一幅图,所有的连接处都有两种可能,前面的依旧是按原来的排列,所以一共有2*f[n-4]+2*f[n-6]+…….+2*f[0]种可能,加起来就推出公式了
#include<stdio.h>
int main()
{
int i,n,sum,sum1=0,sum2=1;
scanf("%d",&n);
if(n%2==1)
printf("0\n");
else
{
for(i=2;i<=n;i+=2)
{
sum=(3*sum2+sum1)%12357;
sum1=(sum1+sum2*2)%12357;
sum2=sum;
}
printf("%d\n",sum);
}
return 0;
}


