一、前言
近年来,深度学习因为在图像,语音等领域得到了很好的实践效果,而被广泛使用。随着深度学习的发展,深度模型越来越大,越来越复杂。伴随而生研究方向是:网络压缩。
网络压缩是指,在不损失网络精度的同时,减少网络的测试时间或者是网络参数的存储空间。本文主要介绍一种通过低秩逼近的方法对网络进行压缩,提高网络前向传播效率。
二、低秩表示
如果把矩阵看成是一个个行或者列向量,秩就是行或者列向量极大无关组中所含向量的个数。

简单来说:Z的样本空间与数据集D的样本空间是等价的。基于低秩表示的假设,在图像去燥等领域取得了不错的效果。本文主要说它在网络压缩里的应用。
三、CNN与网络压缩
本文介绍的网络压缩方法只适用于卷积层和全连接层。在介绍网络压缩之前,我们首先对CNN网络有一个大概的了解。
CNN基本包括以下一些Layer:conv /bn / action /pool /fc 等。其中pool/action 层正常是没有参数的;因此,我们所说的关于CNN网络的压缩主要是指针对conv 和 fc而言。
网络压缩的目的是:1 提高运行时间效率;2 降低模型空间存储大小;
对于CNN网络来说:1 网络参数的90%来源于全连接层;2 网络运行时间的90%来源于卷积层;3 卷积层的时间大部分都消耗在前面几层(

四、低秩逼近的网络压缩
卷积层为例:

卷积W可以看成是f个w(k*k*c)的卷积作用于输入的featuremap上。
假设这f个卷积满足低秩表示的约束,我们可以找到M个(M<f)w(kkc)的卷积,通过线性组合,得到近似等价的输出。
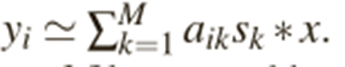
接下来:我们看看运算量的变化:
原始卷积计算量:O(KKFWH)
新卷积计算量:O((KKM+MF)WH)
如果使得新卷积的计算量小于原始卷积的计算量,则需要满足:

五、低秩逼近网络压缩的具体解决方案
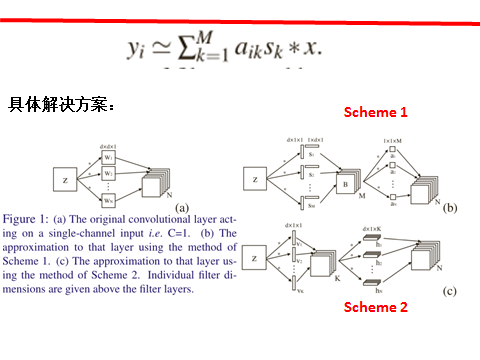
上面这一页PPT给出了常用的两种方法,总的来说都是讲一层卷积拆分成两层卷积。第一类方式是严格按照低秩逼近的意义,先得到M个低秩的featuremap 然后对着M个featuremap进行1*1的卷积操作,从而得到与原卷积非常近似的输出。第二类方法是从目标出发,中间产生多少的featurenmap并不是重点,重点是如何尽量确保进过两次卷积输出的featurenmap的值与原卷积输出的值近似相等。
模型优化:第一类优化

优化的目标是已知W,计算A和S,具体如下,利用交替迭代的方法解算A和S:

模型优化:第二类优化

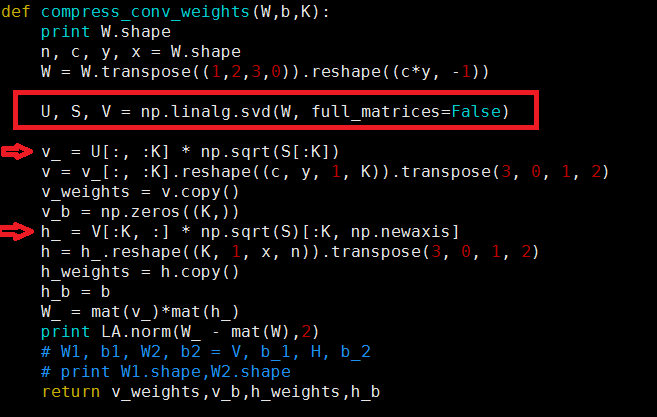
第二类优化的目的是将W拆分为两个矩阵的乘积,具体计算同样可以利用方法1中迭代优化的算法。但是,已有的矩阵分解已经提供了这种方法的一种算法近似解,如SVD分解,如上图。
关于代码实现,非常简单:简单截图如下:
总结:低秩逼近的方法用于全连接层效果较好,但是对运行时间提升空间不是很大。一般能达到1.5倍。将低秩逼近的压缩算法用于卷积层时,会出现误差累积的效果,对最后精度损失影像较大,需要对网络进行逐层的微调,费时费力。



