从分治的角度理解FFT

　　本随笔的目标主要在于解决两个多项式相乘得到新多项式的问题，我们举一个例子，A(x)是n-1次的，B(x)是n-1次，那么我们用C(x) = A(x) * B(x),如果要完整的求出C(x)的系数，采取暴力手段的话一般需要N^2的量级，希望在讲完这一章的内容之后，我们都可以知道怎么样在nlogn的复杂度内解决这个问题。

　　我们把整个算法分成若干步，来计算C(x) = c0 + c1*x + c2*x^2 + ... + c(2n-1)*x^(2n-1)的系数c0~c(2n-1),其中C(x)是由A(x)和B(x)相乘得到的。

　　我们先介绍一下单位根的内容，学过复数的同学们应该都知道，形如a + bi的复数可以用三角式表达r(cosx + isinx)，如果r = 1，我们就得到了一个单位复数cosx + isinx，为了记号的方便，我们把这个复数记作e(x)，其中x是[0,2pi)中的实数。于是e(0) = 1，e(x)^2 = e(2x)，e(x) * e(y) = e(x + y)都容易得到；如果x = k*pi/2n，我们立刻得到e(x)^0 + e(x)^1 + ... + e(x)^(2n-1) = 2n 或者0，其中2n在k = 0的时候取到，0在其他情况下取到。大概就只需要这些知识。

　　第一步，我们来介绍对一个多项式A(x)，快速求出其在x = e(k * pi / 2n)上的函数值，其中k = 0,1,2,...,2n-1。我们不妨设A(x) = a0 + a1x + a2x^2 + ....+a(n-1)x^(n-1)，我们可以把A(x)里面的奇数次和偶数次分开：a0 + a2x^2 + a4x^4 + ..... 和 a1x + a3x^3 + ..... ；我们换一个写法就是A(x) = a0 + a2x^2 + a4*x^4 + ...  + x * (a1 + a3*x^2 + ...)，我们不难发现每个括号里面凡是带x的都是偶数次幂，而且项数不超过ceil(n/2)，我们容易想到把A(x)写成A1(x^2) + x * A2(x^2)的形式!至此我们找到了分治的方法。由于有2n个x要求值，设T(n)为A的次数为n时的复杂度，所以我们可以得到T(n) = 2 * T(n/2) + O(n)，其中O(n)是由于有O(n)个x需要合并在一起。根据主定理，于是我们可以在O(nlogn)时间内完成这个任务！

　　第二步，根据第一步我们可以得到A(x)和B(x)在x = e(k * pi / 2n)上的值，然后用C(x) = A(x) * B(x)的到对应的C的函数值，这一步只要O(n)的时间。我们不妨令p(k) = e(k * pi / 2n)，并且令C(p(k)) = dk，所以我们可以构造一个新的多项式D(x) = d0 + d1 * x + ... + d(2n-1) * x^(2n-1)。复杂度是O(n)。

　　第三步，根据第二步我们可以计算出D(p(k)) = Dk。复杂度是O(nlogn).

　　接下来就是激动人心的时刻，我们有D0 = c0, ci = D(2n-i) / 2n (1 <= i < 2n），于是可以在O(n)的时间内完成！具体的证明见下图(记e = e(1), 则e(k) = e^k)：

　　根据上面的过程我们可以列出下面的式子：

　　

 

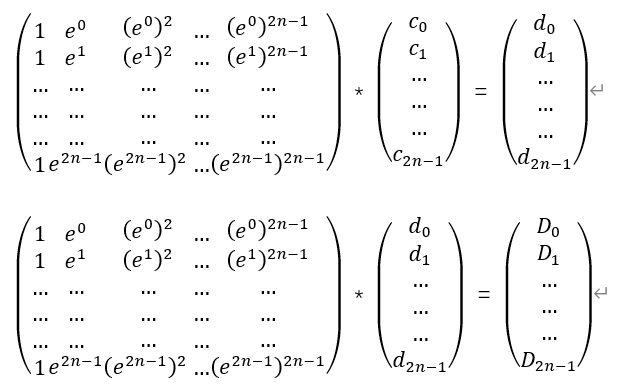
　　结合起来就是：

　　

 

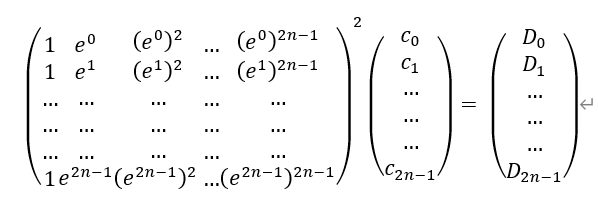
　　令P为那个大矩阵，我们容易计算P*P的(i,j)元有两种情况，如果i + j - 2模2n为0，答案是2n，否则一律为0。（留给读者思考）

　　最后我们得到：

 

 　　结论自鸣。