红黑树和AVL树笔记摘要
昨天晚上与今天重温了一下RB树和AVL树的部分，（其实是之前《索引笔记摘要》的FLAG)把觉得重要的一些东西写在这里和大家分享，不对的地方请不吝指正。
先谈谈红黑树。红黑树诞生的背景是为了保证插入、删除、查找的效率都是在O(logn)，防止由于产生畸形的BST树对效率产生巨大影响。
红黑树的定义：每个结点是红色或者黑色，首尾都是黑色（根节点和扩充的叶节点），父子结点不允许红红连续，任意结点到叶节点的任意路径包括相同数目的黑节点数目（不包括自己，包括扩充的叶节点）。【注意】空树叶也看成结点
红黑树里面结点X的阶rank(X)定义为该节点到外部结点路径上黑色结点的数目，不包括X,但是包括外部结点；根的阶称为红黑树的阶。红黑树是满二叉树，k阶红黑树的根节点到外部结点的路径长度范围是[k, 2k]，树高介于[k + 1, 2k + 1]
红黑树的一个重要性质：n个（内部）结点的树的高度不超过2*log(n+1) + 1(log以2为底，下略)，证明如下：设红黑树为k阶的，则h <= 2*k+1，又n >= 2^k – 1，带入就可以得到h <= 2*log(n+1) + 1，所以说明红黑树的检索一定是O(logn)的，这个性质非常好！
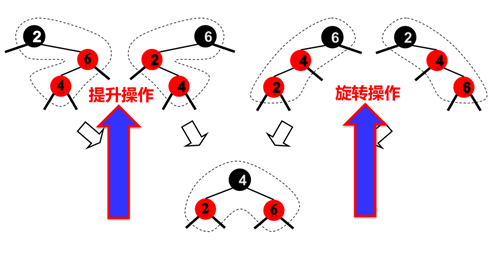
红黑树的插入：待插入结点记为p，p的颜色先弄成红色，找到待插入位置【1】如果p的父节点是黑色的，那么就直接完成了插入【2】否则p的父节点是红色的（红红相连），考虑叔父结点的颜色【2.1】如果叔父结点是黑色或NIL的话，就把待插入结点p，p的父节点，p的叔父结点提升（双旋）/旋转成一个二叉的结构（可以看下图理解），就可以解决插入；【2.2】如果叔父结点是红色，就考虑把p的父节点和叔父结点都变成黑色，p的祖先如果不是根节点就变成红色并且对其进行双红检查，递归向上，直到根节点或者某个结点不满足双红的条件就停止检查。不难发现插入的效率也是比较高的，也是O(logn)。
【2.1】中提升或旋转方法如下：
【2.2】中图示如下：
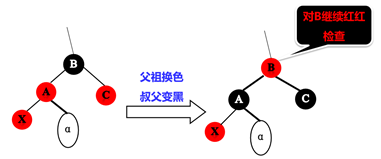
红黑树的插入总结一下就是：红黑旋转，阶数平衡，停止；红红变色，双红递归，继续。
红黑树的删除：考虑当前结点的孩子中叶子结点的数目，如果为0的话说明这个结点的孩子结点都是内部结点，先从右子树里面找后继并代替（变值不变色），然后删除对应的那个后继结点，否则其孩子结点中至少一个外部节点。
1）只有一个外部结点，设待删除结点是x，x的左孩子是外部节点，右孩子是y（内部结点），x的父亲是z，由于任意结点的黑色路径等长，所以y为红色，则x为黑色，把y直接提到x的位置，并且把y的颜色变成黑色就可以了。
2）有两个外部结点，如果待删除的是红色结点就直接删除，否则待删除结点以及其两个孩子（都是外部结点）是黑色，这个结点称为双黑结点。如果兄弟结点是红色的话，那么进行旋转，把兄弟结点提成新根节点并且置黑，新根节点的左孩子为红色，从而对应的双黑结点的右兄弟为黑色，这一步只是为了划归到两种更基本的情况。
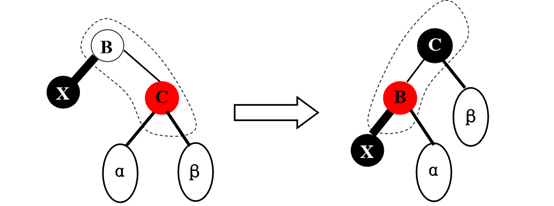
2.1 双黑结点的兄弟结点C也是双黑结点，设x的父节点为B，把C弄成红色，B弄成黑色，（B原来为红色就结束）否则就进行双黑调整。
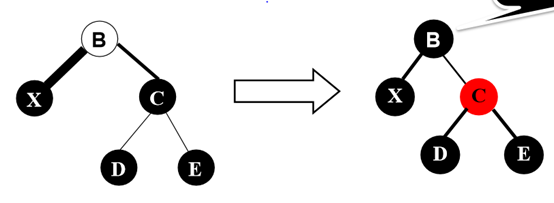
2.2 双黑结点C的子结点有红色，旋转重构：侄子红节点八字外撇和侄子红节点同边顺。要点是把待删除结点x，x的右兄弟以及其红色结点的孩子按照BST进行重构，并且要保证根不变色，父兄全黑的原则。
八字撇：
同边顺：
AVL树
AVL树是一种自适应的树，类似于红黑树，它对每个结点提出了“平衡因子“的概念，此处我们定义一个结点的平衡因子大小是右子树的高度减去左子树的高度。AVL树通过保证各个结点的平衡因子为-1或1来使得整个树结构近似的平衡，从而保证各种操作的效率稳定在O(logn)。
先来估计n个结点的AVL树高度，不难发现1个结点的AVL树高度为1，2个结点为2，3个结点为2（不允许链表形式），4个结点为3……，于是我们不妨考虑一棵高度为h的AVL树的最大结点数目F(h)，F(h) = 1 + 2 * F(h-1), F(1) = 1得到F(h) = 2^h – 1，设高度为h的AVL树的最小结点数目为f(h)，f(1) = 1, f(2) = 2, f(h) = 1 + f(h-1) + f(h-2)，得到f(n) 为“斐波那契数列的第n+2项再减1” , 由F(h) >= n >= f(h)，简单运算可以得到h = O(logn)。于是AVL树的检索效率是严格在O(logn)量级的。
再来考察插入和删除操作。插入或删除的时候从当前结点开始向上更新平衡因子，对于那些平衡因子的绝对值大于1的结点要进行调整，主要方法有两个：左旋转和右旋转。同时要注意在调整过程中，如果当前结点为根的树在调整前后的高度没有变化，就不需要再向上传递调整的信号了。
谈谈具体的调整方法，【1】如果x结点左重，左孩子为y，【1.1】如果y也左重的话，就把y提升为根结点，具体操作就是一个右旋转；【1.2】如果y右重，就把y的右孩子提升为x所在子树的根结点，y作为左孩子，x作为右孩子，更新相关平衡因子，值得注意的是此时相当于从上到下先左旋转，后右旋转。X结点右重时同理可得。具体的操作不再演示。
红黑树和AVL树的比较：红黑树的统计性能比AVL树要好而且容易实现。
