Slope Trick
原理
若一个函数满足:
- 连续
- 分段线性
- 凸性
则称它是折线函数。折线函数可以使用 Slope Trick 来快速维护。
我们发现我们可以仅通过记录转折点,转折点处斜率变化,以及一侧的直线即可维护出整个函数。具体而言每一个转折点出现,我们就认为该函数在该点斜率变化了 1.
举个例子,对于如下函数:
我们可以用 \([\{0, 2, 2\}, 2x + 3]\) 来表示。
若 \(f(x)\) 和 \(g(x)\) 是两个凹凸性相同的满足要求的函数,则 \(h(x) = f(x) + g(x)\) 也是与它们凹凸性相同且满足要求的函数。同时 \(S_h = S_f \cup S_g, F_h = F_f + F_g\)
CF713C
题意
给定一个长为 \(n\) 的数组,每次操作可以把任意一个元素 \(+1\) 或 \(-1\),求使得其变成严格递增的最小操作次数。
\(n \leq 10^5, a_i \leq 10^9\)。
题解
由于值域比较大,直接 dp 不太能做。考虑设 \(b_i = a_i - i\),原问题即转化为求将 \(b\) 转化为非严格递增的最小操作次数。容易发现最终序列中的值一定都属于 \(b\) 序列。
设 \(f_{i, j}\) 表示 dp 到第 \(i\) 位,第 \(i\) 位值为 \(b_j\) 的最小操作次数。则 \(f_{i,j} = \min_{k \leq j} \{ f_{i - 1, k} \} + |b_i - b_j|\)。
设 \(g_{i, j} = \min_{k \leq j} \{ f_{i, k} \}\),则 \(f_{i,j} = g_{i - 1, j} + |b_i - b_j|\)。
设 \(F_i(x) = f_{i, j}, G_i(x) = g_{i, j}\)。容易发现 \(F_i(x)\) 和 \(G_i(x)\) 是折线函数。具体证明考虑归纳法。
首先 \(F_0\) 和 \(G_0\) 必定是凸的。当 \(G_{i - 1}\) 是凸的,其加上一个凹凸性相同的绝对值函数得到 \(F_i\) 也是凸的。具体原因考虑二阶导非负。对于 \(F_i\) 前缀取 \(\min\) 即得到 \(G_i\),所以 \(G_i\) 也是凸的。
现在考虑用 Slope Trick 来维护 \(F_i\) 和 \(G_i\)。易得答案为 \(G_n\) 的无穷远处对应的值。
因为是前缀取 \(\min\) 所以 \(G_i\) 的最右侧函数的斜率为 \(0\)。且前面的函数与 \(F_i\) 重合。
初始时 \(G_0\) 恒为 0, 表示为 \([\emptyset, 0]\)。对 \(G_{i - 1}\),加上一个绝对值函数 \(|x - b_i|\) 即在转折点集合中插入点两次点 \(b_i\),并将最右端的函数斜率 \(+1\),即可转化成 \(F_i\)。再将 \(F_i\) 最右侧推平即可得到 \(G_i\)。
现在来关注一下 \(G_i\) 无穷远点的值的变化,即答案的变化。因为最右侧斜率为 \(0\),所以无穷远点的答案等价于斜率为 0 的转折点处的答案。上一张图通俗的解释一下。
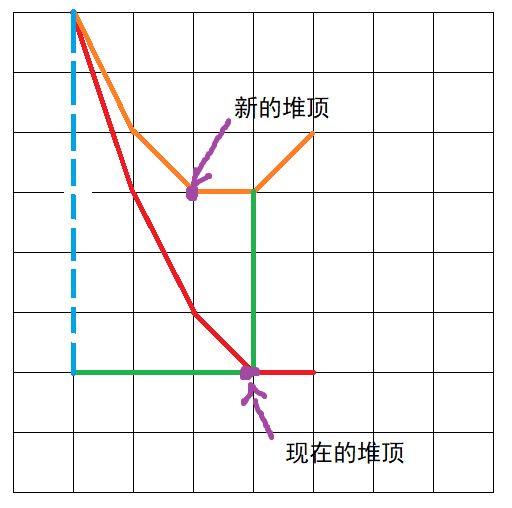
变化量即 \(f_r'(top) - f_r'(b_i)\),此题中即为 \(top - b_i\)。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read() {
int res = 0, f = 1; char ch;
while((ch = getchar()) && (ch < '0' || ch > '9') && ch != '-');
(ch == '-') ? f = -1 : res = ch - '0';
while((ch = getchar()) && ch >= '0' && ch <= '9') res = (res << 3) + (res << 1) + ch - '0';
return res * f;
}
const int MAXN = 1e5 + 5;
int n;
priority_queue<int> q;
signed main() {
n = read();
int res = 0;
for(int i = 1, x; i <= n; i++) {
x = read() - i;
q.push(x); q.push(x);
res += q.top() - x; q.pop();
}
printf("%lld\n",res);
return 0;
}
ABC217H
题意
有一个游戏,发生在一条数轴上,最初 \(0\) 时刻,Snuke 在 \(0\) 号节点。
每过一个时刻,你可以选择向正方向或负方向移动一格,或者不移动。
接下来有 \(n\) 个事件,每一个事件用 \(T_i,D_i,X_i\) 描述,其中 \(T_i\) 表示事件发生时刻,假设 Snuke 此时在 \(p\) 点:
- 若 \(D_i=0\),Snuke 将会受到 \(\max\{0,X_i-p\}\) 的伤害。
- 若 \(D_i=1\),Snuke 将会受到 \(\max\{0,p-X_i\}\) 的伤害。
请问 \(n\) 次事件之后 Snuke 受到的伤害量的最小值。
- \(1\le n\le 2\times 10^5\)。
- \(1\le T_1\le T_2\le \cdots\le T_n\le 10^9\)。
- \(\forall i\in[1,n],D_{i}\in\{0,1\},-10^9\le X_i\le 10^9\)。
题解
设 \(H_i(x)\) 表示在 \(i\) 时刻位于 \(x\) 收到的伤害,设 \(f_{i, j}\) 表示在 \(i\) 时刻位于 \(j\) 受到的最小伤害和。
设 \(t = T_i - T_{i - 1}\),有 \(f_{i, j} = \min_{j - t \leq k \leq j + t} \{f_{i - 1, k}\} + H_i(j)\)
此题与上一题的差别在于函数取 \(\min\) 的是一段区间。换句话说,\(F_i\) 斜率为 0 的点位于中间,不存在某一侧的函数斜率为 0。
于是我们可以考虑从斜率为 \(0\) 的点的位置将函数剖成两半,\(L_i\) 和 \(R_i\)。它们分别有一侧斜率为 0。
考虑如何转移。首先因为\(L_i\) 单调递减,\(R_i\) 单调递增,所以将 \(L\) 向左平移 \(t\),将 \(R\) 向右平移 \(t\)。具体实现整体打标机即可。
设斜率为 \(0\) 的段为 \([l, r]\),当前插入点为 \(x\),以 \(D_i = 0\) 为例。此时插入一个点等价于把它左侧所有点的斜率 \(-1\),分两种情况讨论。
- \(x \leq r\),此时插入 \(x\) 并不会改变答案。
- \(x > r\),此时插入 \(x\) 会对斜率为 0 的区间答案产生影响。具体而言,答案会增加 \(x - r\),斜率为 \(0\) 的点变为斜率为 \(-1\) 的区间,斜率为 \(1\) 的区间变为斜率为 \(0\) 的区间。所以把 \(R\) 的堆顶弹出压入到 \(L\) 中。

