排列组合基础

修改日志

• 2022.11.5 重构整篇文章

定义

组合数又称二项式系数，有基本定义：

$$\binom{n}{m} = \frac{n!}{m!(n - m)!}\quad(n\in\mathbf{N},m\in\mathbf{N})$$

然后我们定义下降幂：

$$n^{\underline{m}} = \prod_{i = 0}^{m - 1}(n - i) = n \cdot (n - 1)^{\underline{(m - 1)}}$$

由此重新定义组合数：

$$\binom{n}{m}=\frac{n^{\underline{m}}}{m!}\quad(n\in\mathbf{C},m\in\mathbf{N})$$

同时有规定：

$$0^0 = 0! = x^{\underline{0}} = 1$$

基础技巧

加法原理

有 $n$ 类元素，第 $i$ 类元素有 $a_i$ 个，从所有类中选出一个元素的方案数为 $\sum_{i = 1}^{n} a_i$。

乘法原理

有 $n$ 类元素，第 $i$ 类元素有 $a_i$ 个，从每一类中都选出一个元素的方案数为 $\prod_{i = 1}^{n} a_i$。

插板法

用于求给相同元素分组的方案数的一种技巧。
即将 $n$ 个相同元素分成 $m$ 个集合（不保证每种集合都非空），集合与集合之间识为不同。
问题等价与在 $n$ 个元素中插入 $m - 1$ 个板，板为两个集合的分割，由此得出插板法的公式：$\binom{n + m - 1}{n}$

排列组合变种

多重集的排列数

又名 多重组合数。
设 $S = {n_1 \cdot a_1, n_2 \cdot a_2, \dots, n_k \cdot a_k}$ 表示由 $n_i$ 个 $a_i$ 组成的多重集, $n = \sum_{i = 1}^{k}n_i$。$S$ 的全排列个数可用多重组合数符号表示为

$$\binom{n}{n_1, n_2, \dots, n_k} = \frac{n!}{\prod_{i = 1}^{k}n_i !}$$

这个也被称为多项式系数，其等价与如下二项式系数的乘积：

$$\binom{n_1 + n_2 + \dots + n_k}{n_2 + n_3 + \dots + n_m}\binom{n_2 + \dots + n_k}{n_3 + \dots + n_m}\dots \binom{n_{m - 1} + n_m}{n_m}\binom{n_m}{0}$$

多重集的组合数

设 $S = {n_1 \cdot a_1, n_2 \cdot a_2, \dots, n_k \cdot a_k}$，从 $S$ 中选出 $r(\forall i \in [1,k], r < n_i)$ 个元素的方案数为可重集的组合数。等价于 $\sum_{i = 1}^{k}n_i = r$ 的非负整数解的个数，用插板法可得答案为 $\binom{r + k - 1}{k - 1}$。

若取任意非负整数 $r$ 个元素，则问题等价于求解带限制的线性方程解的个数：

$$\sum_{i = 1}^{k} x_i = r,\quad \forall i \in [1, k], x_i \leq n_i$$

补集转化，用所有方案数减去不合法方案数，每次钦定 $p$ 种元素超出限制，容斥一下可得答案等于：

$$\sum_{p = 0}^{k}(-1)^p\sum_{S'\subseteq S \wedge |S'|=p}\binom{k+r-1-\sum (a_{i}^{'}+1)}{k - 1}$$

圆排列

$n$ 个元素围成一圈，两种方案不同当且仅当两种方案不能通过顺或逆时针旋转后相同，所有排列的方案数记为 $Q_{n}^{n}$。考虑对于任意一个圆排列，钦定其从任意位置断开都能形成一个新的一般的排列，所以：

$$Q_{n}^{n} = \frac{A_{n}^{n}}{n} = (n - 1)!$$

同理可得部分圆排列为：

$$Q_{n}^{r} = \frac{A_{n}^{r}}{r} = \frac{n!}{r \times (n - r)!}$$

错排

求长度为 $n$ 的 $a$ 排列满足 $a_i \neq i$ 的方案数 $D_n$。
首先显然有 $D_0 = 1, D_1 = 0$，现在考虑新加入一个数产生的贡献。
每新加入一个元素有两种选择：

• 前 $(n - 1)$ 个数已经满足要求，从中任意选择一个元素与之交换，有 $(n - 1)$ 种选择。
• 前 $(n - 1)$ 个数有一个数不满足要求，与之交换，有 $(n - 1)$ 种可能。

所以 $D_n = (n - 1)(D_{n - 1} + D_{n - 2})$

性质和公式

对称公式

$$\binom{n}{k}=\binom{n}{n-k} \quad k \in \mathbf{N}$$

相当与对选出的集合与全集取补集。（对称性）

加法公式

$$\binom{n}{k}=\binom{n-1}{k}+\binom{n-1}{k-1} \quad n,k \in \mathbf{N}, k \leq n$$

其组合意义为钦定最后一个数选或不选的方案数相加。

吸收公式

$$k\binom{n}{k} = n \binom{n - 1}{k - 1}, (n - k)\binom{n}{k} = n\binom{n - 1}{k} \quad k \in \mathbf{Z}$$

前式的组合意义为从 $n$ 个元素中选出 $k$ 个再钦定一个的方案数等价于从 $n$ 个元素中先钦定一个再在剩下的 $n - 1$ 个元素中选出 $k - 1$ 个。
后式两边都使用一次对称公式就和前式等价。

上指标反转

$$\binom{n}{k} = (-1)^k\binom{k - n - 1}{k} \quad k \in \mathbf{Z}$$

结合定义是，就是将 $n^{\underline{k}}$ 每一项取负。

奇技淫巧

$$\binom{n}{m}\binom{m}{k} = \binom{n}{k}\binom{n - k}{m - k}$$

其组合意义为从含有 $n$ 个元素的集合 $A$ 中选出一个大小为 $m$ 的子集 $B$，再从集合 $B$ 中选出大小为 $k$ 的子集 $C$。其等价与先从 $A$ 中选出 $C$ 再从 $C$ 与 $A$ 的补集中选出集合 $B'$，集合 $B'$ 和集合 $C$ 取并集就是 $B$。

组合数+求和

一行之和

$$\sum_{i=0}^{n}\binom{n}{i}=2^n \quad n \in \mathbf{N}$$

其组合意义为所有的选数方案恰好对应了每一个数选或不选的方案数。

上指标求和

$$\sum_{i=0}^{n}\binom{i}{k}=\binom{n+1}{k+1}$$

其组合意义为 从 $n + 1$ 个数中选择 $k + 1$ 个数的方案数。其等价于钦定最后一个选择的元素是第 $i + 1$ 个，在前 $i$ 个数中选择 $k$ 个数的方案数之和。
其对应在杨辉三角上如图所示：

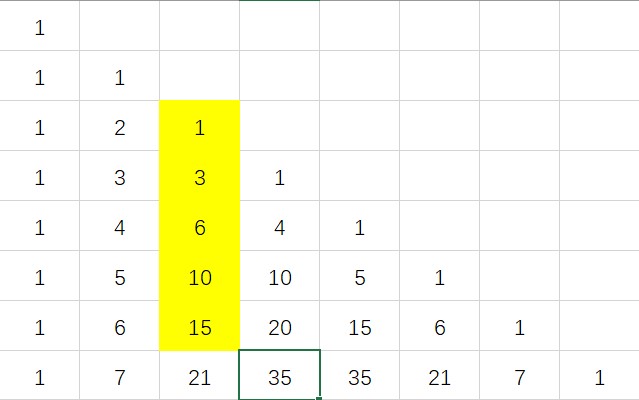
绿色框中的数等于黄色的选中的数相加的和。
具体证明可结合杨辉三角，添加 $\binom{0}{m + 1} = 0$ 项，再利用加法公式。

平行求和

$$\sum_{i=0}^{k}\binom{n+i}{i}=\binom{n+k+1}{k}$$

平行求和可将每一项利用对称性转化为上指标求和。
其对应在杨辉三角上如图所示：

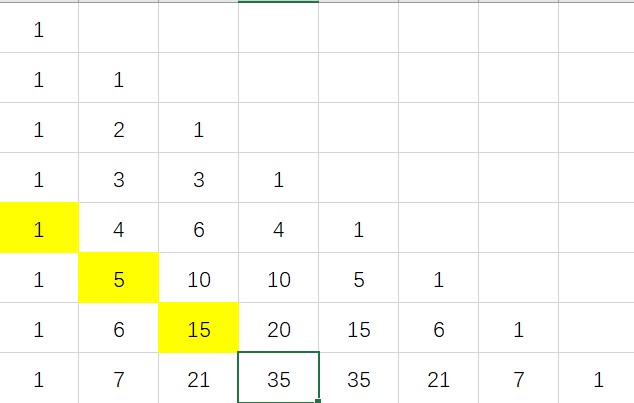
绿色框中的数等于黄色的选中的数相加的和。
具体证明可结合杨辉三角，利用 $\binom{n}{0} = \binom{n + 1}{0}$，再利用加法公式。

交错求和

$$\sum_{k \leq m}(-1)^k \binom{r}{k} = (-1)^m\binom{r - 1}{m} \quad m \in \mathbf{Z}$$

证明考虑上指标反转后平行求和再上指标反转。

恒等式一（扩展牛顿二项式定理）

$$(x + y)^r = \sum_{k} \binom{r}{k}x^k y^{r - k}$$

当 $r \in \mathbf{N}$ 时，是牛顿二项式定理，但当 $|\frac{x}{y}| < 1, r \in \mathbf{R}$ 时也成立。
证明第一种情况可以直接考虑组合意义，证明第二种情况需要用泰勒级数。

特殊情况，容斥原理常用：

$$\sum_{i=0}^{n}\binom{n}{i}(-1)^i=((-1)+1)^n=[n=0]$$

恒等式二（范德蒙德卷积）

$$\sum_{k}\binom{r}{k}\binom{s}{n - k} = \binom{r + s}{m} \quad n \in \mathbf{Z}$$

其组合意义为从大小为 $r$ 和大小为 $s$ 的两个集合中取出 $m$ 个元素，等价与枚举从 $r$ 集合中取出 $i$ 个元素，再在 $s$ 集合中取出剩余的元素。

恒等式三

$$\sum_{k \leq m} \binom{m + r}{k} x^k y^{m - k} = \sum_{k \leq m}\binom{-r}{k}(-x)^k (x+y)^{m - k} \quad m \in \mathbf{Z}$$

证明考虑数学归纳法，对于 $m < 0$，左右都为 $0$。对于 $m = 0$，左右都为 $1$。
设左式等于 $f_m$，有：

$$\begin{align*} f_m & = \sum_{k \leq m} \binom{m + r}{k} x^k y^{m - k}\\ & = \sum_{k \leq m} \binom{m + r - 1}{k} x^k y^{m - k} + \sum_{k \leq m} \binom{m + r - 1}{k - 1} x^k y^{m - k}\\ & = (y \cdot f_{m - 1} + \binom{m + r - 1}{m}x^m)+x \cdot f_{m - 1}\\ & = (y \cdot f_{m - 1} + \binom{m + r - 1}{m}x^m)+x \cdot f_{m - 1}\\ & = (x + y)f_{m - 1} + \binom{-r}{m}(-x)^m \end{align*}$$

设右式等于 $g_m$，有：

$$g_{m - 1} = \sum_{k \leq m - 1}\binom{-r}{k}(-x)^k (x+y)^{m - k - 1}$$

$$g_{m} = \sum_{k \leq m}\binom{-r}{k}(-x)^k (x+y)^{m - k}$$

$$g_{m} = (x + y)g_{m - 1} + \binom{-r}{m}(-x)^m$$

由于左右两边递推方式相同，所以当 $m - 1$ 成立时，$m$ 也成立，得证。

当 $x = -1, y = 1$ 时，等价于交错求和。

恒等式四

$$\sum_{i = 0}^{n}\binom{n - i}{i} = F_n$$

直接归纳证明即可。

__EOF__

本文作者：zym417
本文链接：https://www.cnblogs.com/zym417/p/16421140.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！