无监督聚类算法K-Means

转自：作者：LY豪
链接：https://www.jianshu.com/p/caef1926adf7

聚类

聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集成为一个“簇”。通过这样的划分，每个簇可能对应于一些潜在的概念（也就是类别），如“浅色瓜” “深色瓜”，“有籽瓜” “无籽瓜”，甚至“本地瓜” “外地瓜”等；需说明的是，这些概念对聚类算法而言事先是未知的，聚类过程仅能自动形成簇结构，簇对应的概念语义由使用者来把握和命名。

聚类和分类的区别？

聚类是无监督的学习算法，分类是有监督的学习算法。所谓有监督就是有已知标签的训练集（也就是说提前知道训练集里的数据属于哪个类别），机器学习算法在训练集上学习到相应的参数，构建模型，然后应用到测试集上。而聚类算法是没有标签的，聚类的时候，我们并不关心某一类是什么，我们需要实现的目标只是把相似的东西聚到一起。

性能度量

聚类的目的是把相似的样本聚到一起，而将不相似的样本分开，类似于“物以类聚”，很直观的想法是同一个簇中的相似度要尽可能高，而簇与簇之间的相似度要尽可能的低。
性能度量大概可分为两类： 一是外部指标， 二是内部指标 。
外部指标：将聚类结果和某个“参考模型”进行比较。
内部指标：不利用任何参考模型，直接考察聚类结果。

K-Means的原理

对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大

K-Means算法

给定样本集D，k-means算法针对聚类所得簇划分C最小化平方误差。

 

 

这条公式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，E值越小则簇内样本相似度越高。
最小化上面的公式并不容易，找到它的最优解需考察样本集D内所有可能的簇划分，这是一个NP难问题。因此，k-means算法采用了贪心策略，通过迭代优化来近似求解上面的公式。算法流程如下：

 

 

其中第一行对均值向量进行初始化，在第4-8行与第9-16行依次对当前簇划分及均值向量迭代更新，若迭代更新后聚类结果保持不变，则在第18行将当前簇划分结果返回。

 

下面以西瓜数据集4.0为例来演示k-means算法的学习过程。我们将编号为i的样本称为xi，这是一个包含“密度”与“含糖率”两个属性值的二维向量。

 

 

假定簇数k=3，算法开始是随机选取三个样本x6,x12,x27作为初始均值向量，即

 

 

 

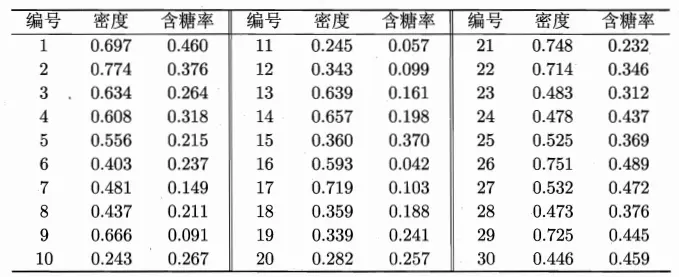
考察样本x1=（0.697；0.460），它与当前均值向量u1，u2，u3的距离分别是0.369，0.506，0.166，因此x1将被划入簇C3中。类似的，对数据集中所有的样本考察一遍后，可得当前簇划分为

 

 

于是，可从C1，C2，C3分别求出新的均值向量

 

 

更新当前均值向量后，不断重复上述过程，如下图所示，第五轮迭代产生的结果与第四轮迭代相同，于是算法停止，得到最终的簇划分。

 

 

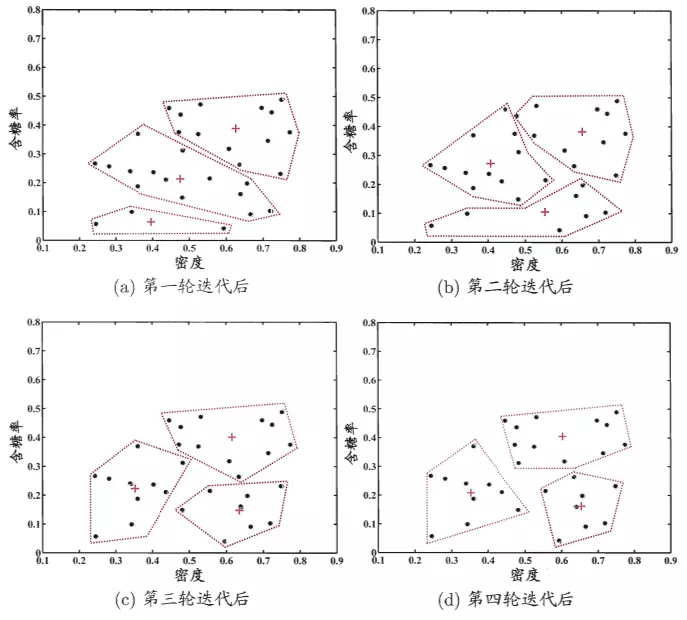
K-Means与KNN

初学者会很容易就把K-Means和KNN搞混，其实两者的差别还是很大的。
K-Means是无监督学习的聚类算法，没有样本输出；而KNN是监督学习的分类算法，有对应的类别输出。KNN基本不需要训练，对测试集里面的点，只需要找到在训练集中最近的k个点，用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程，找到k个类别的最佳质心，从而决定样本的簇类别。
当然，两者也有一些相似点，两个算法都包含一个过程，即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。

K-Means的优点与缺点

优点：
简单，易于理解和实现；收敛快，一般仅需5-10次迭代即可，高效
缺点：
1，对K值得选取把握不同对结果有很大的不同
2，对于初始点的选取敏感，不同的随机初始点得到的聚类结果可能完全不同
3，对于不是凸的数据集比较难收敛
4，对噪点过于敏感，因为算法是根据基于均值的
5，结果不一定是全局最优，只能保证局部最优
6，对球形簇的分组效果较好，对非球型簇、不同尺寸、不同密度的簇分组效果不好。

代码部分

读取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
dataset = pd.read_csv('watermelon_4.csv', delimiter=",")
data = dataset.values
print(dataset)

K-Means算法

import random
def distance(x1, x2):
    return sum((x1-x2)**2)
def Kmeans(D,K,maxIter):
    m, n = np.shape(D)
    if K >= m:
        return D
    initSet = set()
    curK = K
    while(curK>0):  # 随机选取k个样本
        randomInt = random.randint(0, m-1)
        if randomInt not in initSet:
            curK -= 1
            initSet.add(randomInt)
    U = D[list(initSet), :]  # 均值向量
    C = np.zeros(m)
    curIter = maxIter
    while curIter > 0:
        curIter -= 1
        for i in range(m):
            p = 0
            minDistance = distance(D[i], U[0])
            for j in range(1, K):
                if distance(D[i], U[j]) < minDistance:
                    p = j
                    minDistance = distance(D[i], U[j])
            C[i] = p
        newU = np.zeros((K, n))
        cnt = np.zeros(K)
        for i in range(m):
            newU[int(C[i])] += D[i]
            cnt[int(C[i])] += 1
        changed = 0
        for i in range(K):
            newU[i] /= cnt[i]
            for j in range(n):
                if U[i, j] != newU[i, j]:
                    changed = 1
                    U[i, j] = newU[i, j]
        if changed == 0:
            return U, C, maxIter-curIter
    return U, C, maxIter-curIter

作图查看结果

U, C, iter = Kmeans(data,3,10)
# print(U)
# print(C)
# print(iter)

f1 = plt.figure(1)
plt.title('watermelon_4')
plt.xlabel('density')
plt.ylabel('ratio')
plt.scatter(data[:, 0], data[:, 1], marker='o', color='g', s=50)
plt.scatter(U[:, 0], U[:, 1], marker='o', color='r', s=100)
# plt.xlim(0,1)
# plt.ylim(0,1)
m, n = np.shape(data)
for i in range(m):
    plt.plot([data[i, 0], U[int(C[i]), 0]], [data[i, 1], U[int(C[i]), 1]], "c--", linewidth=0.3)
plt.show()