numpy -- 处理数值型数据 -- 数据分析三剑客

博客地址：https://www.cnblogs.com/zylyehuo/

NumPy(Numerical Python) 是 Python 语言中做科学计算的基础库。重在于数值计算，也是大部分Python科学计算库的基础，多用于在大型、多维数组上执行的数值运算。

开发环境

• anaconda
  • 集成环境：集成好了数据分析和机器学习中所需要的全部环境
  • 安装目录不可以有中文和特殊符号
• jupyter
  • anaconda提供的一个基于浏览器的可视化开发工具

numpy的创建

• 使用np.array()创建
• 使用plt创建
• 使用np的routines函数创建

使用array()创建一个一维数组

import numpy as np
arr = np.array([1,2,3])
arr

array([1, 2, 3])

使用array()创建一个多维数组

arr = np.array([[1,2,3],[4,5,6]])
arr

array([[1, 2, 3],
       [4, 5, 6]])

数组和列表的区别

数组中存储的数据元素类型必须是统一类型
优先级：字符串 > 浮点型 > 整型

arr = np.array([1,2.2,3])
arr

array([1. , 2.2, 3. ])

将外部的一张图片读取加载到numpy数组中，然后尝试改变数组元素的数值查看对原始图片的影响

import matplotlib.pyplot as plt
img_arr = plt.imread('./1.jpg')  # 返回的数组，数组中装载的就是图片内容
plt.imshow(img_arr)  # 将numpy数组进行可视化展示

<matplotlib.image.AxesImage at 0x117fb1b38>

img_arr = img_arr - 100  # 将每一个数组元素都减去100
plt.imshow(img_arr)

<matplotlib.image.AxesImage at 0x1181a6b38>

使用内置函数创建数组

• zero()
• ones()
• linespace()
• arange()
• random系列

np.ones(shape=(3,4))

array([[1., 1., 1., 1.],
       [1., 1., 1., 1.],
       [1., 1., 1., 1.]])

np.linspace(0,100,num=20)  # 一维的等差数列数组

array([  0.        ,   5.26315789,  10.52631579,  15.78947368,
        21.05263158,  26.31578947,  31.57894737,  36.84210526,
        42.10526316,  47.36842105,  52.63157895,  57.89473684,
        63.15789474,  68.42105263,  73.68421053,  78.94736842,
        84.21052632,  89.47368421,  94.73684211, 100.        ])

np.arange(10,50,step=2)  # 一维等差数列

array([10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42,
       44, 46, 48])

np.random.randint(0,100,size=(5,3))

array([[19,  0, 17],
       [72, 29, 13],
       [69, 59, 68],
       [63, 54, 87],
       [70, 64,  0]])

numpy的常用属性

• shape
• ndim
• size
• dtype

arr = np.random.randint(0,100,size=(5,6))
arr

array([[43, 96, 75,  1, 34, 88],
       [96,  2, 17, 34, 26, 57],
       [71, 36, 11, 11, 10, 29],
       [72, 46, 51,  4, 27, 75],
       [80, 42, 27, 55, 19, 43]])

arr.shape  # 返回的是数组的形状

(5, 6)

arr.ndim  # 返回的是数组的维度

2

arr.size  # 返回数组元素的个数

30

arr.dtype  # 返回的是数组元素的类型

dtype('int64')

type(arr)  # 数组的数据类型

numpy.ndarray

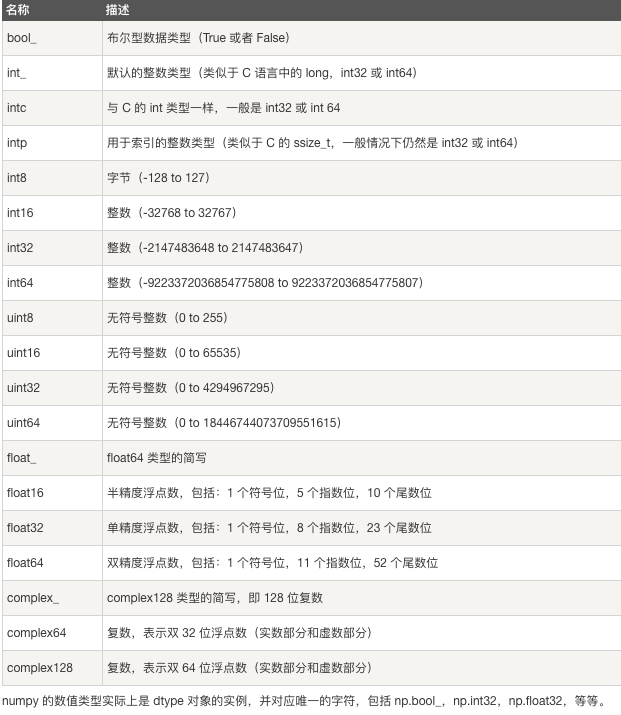
numpy的数据类型

• array(dtype=?):可以设定数据类型
• arr.dtype = '?':可以修改数据类型image.png

• 

arr = np.array([1,2,3])
arr.dtype

dtype('int64')

# 创建一个数组，指定数组元素类型为int32
arr = np.array([1,2,3],dtype='int32')
arr.dtype

dtype('int32')

arr.dtype = 'uint8' #修改数组的元素类型
arr.dtype

dtype('uint8')

numpy的索引和切片操作（重点）

索引操作和列表同理

arr = np.random.randint(1,100,size=(5,6))
arr

array([[69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34],
       [13, 16, 93, 54, 87, 34],
       [ 5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88]])

arr[1]  # 取出了numpy数组中的下标为1的行数据

array([37, 57, 26, 92, 91, 34])

arr[[1,3,4]]  # 取出多行

array([[37, 57, 26, 92, 91, 34],
       [ 5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88]])

切片操作

• 切出前两列数据
• 切出前两行数据
• 切出前两行的前两列的数据
• 数组数据翻转
• 将一张图片上下左右进行翻转操作
• 将图片进行指定区域的裁剪

# 切出arr数组的前两行的数据
arr[0:2]  # arr[行切片]

array([[69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34]])

# 切出arr数组中的前两列
arr[:,0:2]  # arr[行切片,列切片]

array([[69, 80],
       [37, 57],
       [13, 16],
       [ 5, 16],
       [54, 63]])

# 切出前两行的前两列的数据
arr[0:2,0:2]

array([[69, 80],
       [37, 57]])

arr

array([[69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34],
       [13, 16, 93, 54, 87, 34],
       [ 5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88]])

# 将数组的行倒置
arr[::-1]

array([[54, 63, 20, 11, 94, 88],
       [ 5, 16, 47, 66, 51, 12],
       [13, 16, 93, 54, 87, 34],
       [37, 57, 26, 92, 91, 34],
       [69, 80,  7, 90, 31, 44]])

# 将数组的列倒置
arr[:,::-1]

array([[44, 31, 90,  7, 80, 69],
       [34, 91, 92, 26, 57, 37],
       [34, 87, 54, 93, 16, 13],
       [12, 51, 66, 47, 16,  5],
       [88, 94, 11, 20, 63, 54]])

# 所有元素倒置
arr[::-1,::-1]

array([[88, 94, 11, 20, 63, 54],
       [12, 51, 66, 47, 16,  5],
       [34, 87, 54, 93, 16, 13],
       [34, 91, 92, 26, 57, 37],
       [44, 31, 90,  7, 80, 69]])

# 将一张图片进行左右翻转
img_arr = plt.imread('./1.jpg')
plt.imshow(img_arr)

<matplotlib.image.AxesImage at 0x1182c3b00>

img_arr.shape

(300, 450, 3)

plt.imshow(img_arr[:,::-1,:])  # img_arr[行，列，颜色]

<matplotlib.image.AxesImage at 0x11835cb70>

# 图片上下翻转
plt.imshow(img_arr[::-1,:,:])

<matplotlib.image.AxesImage at 0x118437ef0>

# 图片裁剪的功能
plt.imshow(img_arr[66:200,78:300,:])

<matplotlib.image.AxesImage at 0x1187fee48>

变形reshape

arr  # 是一个5行6列的二维数组

array([[69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34],
       [13, 16, 93, 54, 87, 34],
       [ 5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88]])

# 将二维的数组变形成1维
arr_1 = arr.reshape((30,))
arr_1

array([69,80,7,90,31,44,37,57,26,92,91,34,13,16,93,54,87,
       34,5,16,47,66,51,12,54,63,20,11,94,88])

# 将一维变形成多维
arr_1.reshape((6,5))

array([[69, 80,  7, 90, 31],
       [44, 37, 57, 26, 92],
       [91, 34, 13, 16, 93],
       [54, 87, 34,  5, 16],
       [47, 66, 51, 12, 54],
       [63, 20, 11, 94, 88]])

级联操作

• 将多个numpy数组进行横向或者纵向的拼接
• axis轴向的理解
  • 0:列
  • 1:行
• 问题：级联的两个数组维度一样，但是行列个数不一样会如何？

np.concatenate((arr,arr),axis=1)

array([[69, 80,  7, 90, 31, 44, 69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34, 37, 57, 26, 92, 91, 34],
       [13, 16, 93, 54, 87, 34, 13, 16, 93, 54, 87, 34],
       [ 5, 16, 47, 66, 51, 12,  5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88, 54, 63, 20, 11, 94, 88]])

arr_3 = np.concatenate((img_arr,img_arr,img_arr),axis=0)
plt.imshow(arr_3)

<matplotlib.image.AxesImage at 0x118f459b0>

常用的聚合操作

• sum,max,min,mean

arr

array([[69, 80,  7, 90, 31, 44],
       [37, 57, 26, 92, 91, 34],
       [13, 16, 93, 54, 87, 34],
       [ 5, 16, 47, 66, 51, 12],
       [54, 63, 20, 11, 94, 88]])

arr.sum(axis=1)

array([321, 337, 297, 197, 330])

arr.max(axis=1)

array([90, 92, 93, 66, 94])

常用的数学函数

• NumPy 提供了标准的三角函数：sin()、cos()、tan()
• numpy.around(a,decimals) 函数返回指定数字的四舍五入值。
• 参数说明：
  • a: 数组
  • decimals: 舍入的小数位数。 默认值为0。 如果为负，整数将四舍五入到小数点左侧的位置

np.sin(2.5)

0.5984721441039564

np.around(3.84,2)

3.84

常用的统计函数

• numpy.amin() 和 numpy.amax()，用于计算数组中的元素沿指定轴的最小、最大值。
• numpy.ptp():计算数组中元素最大值与最小值的差（最大值 - 最小值）。
• numpy.median() 函数用于计算数组 a 中元素的中位数（中值）
• 标准差std():标准差是一组数据平均值分散程度的一种度量。
  • 公式：std = sqrt(mean((x - x.mean())**2))
  • 如果数组是 [1，2，3，4]，则其平均值为 2.5。 因此，差的平方是 [2.25,0.25,0.25,2.25]，并且其平均值的平方根除以 4，即 sqrt(5/4) ，结果为 1.1180339887498949。
• 方差var()：统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数，即 mean((x - x.mean())** 2)。换句话说，标准差是方差的平方根。

arr[1].std()

26.66718749491384

arr[1].var()

711.138888888889

矩阵相关

• NumPy中包含了一个矩阵库 numpy.matlib，该模块中的函数返回的是一个矩阵，而不是 ndarray 对象。一个 的矩阵是一个由行（row）列（column）元素排列成的矩形阵列。
• numpy.matlib.identity() 函数返回给定大小的单位矩阵。单位矩阵是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为 1，除此以外全都为 0。

eye返回一个标准的单位矩阵

np.eye(6)

array([[1., 0., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0.],
       [0., 0., 1., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0.],
       [0., 0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 0., 1.]])

.T 转置矩阵

arr.T

array([[69, 37, 13,  5, 54],
       [80, 57, 16, 16, 63],
       [ 7, 26, 93, 47, 20],
       [90, 92, 54, 66, 11],
       [31, 91, 87, 51, 94],
       [44, 34, 34, 12, 88]])

矩阵相乘

• numpy.dot(a, b, out=None)
  • a : ndarray 数组
  • b : ndarray 数组

• 

• 第一个矩阵第一行的每个数字（2和1），各自乘以第二个矩阵第一列对应位置的数字（1和1），然后将乘积相加（ 2 x 1 + 1 x 1），得到结果矩阵左上角的那个值3。也就是说，结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。
• 线性代数基于矩阵的推导: https://www.cnblogs.com/alantu2018/p/8528299.html

a1 = np.array([[2,1],[4,3]])
a2 = np.array([[1,2],[1,0]])
np.dot(a1,a2)

array([[3, 4],
       [7, 8]])