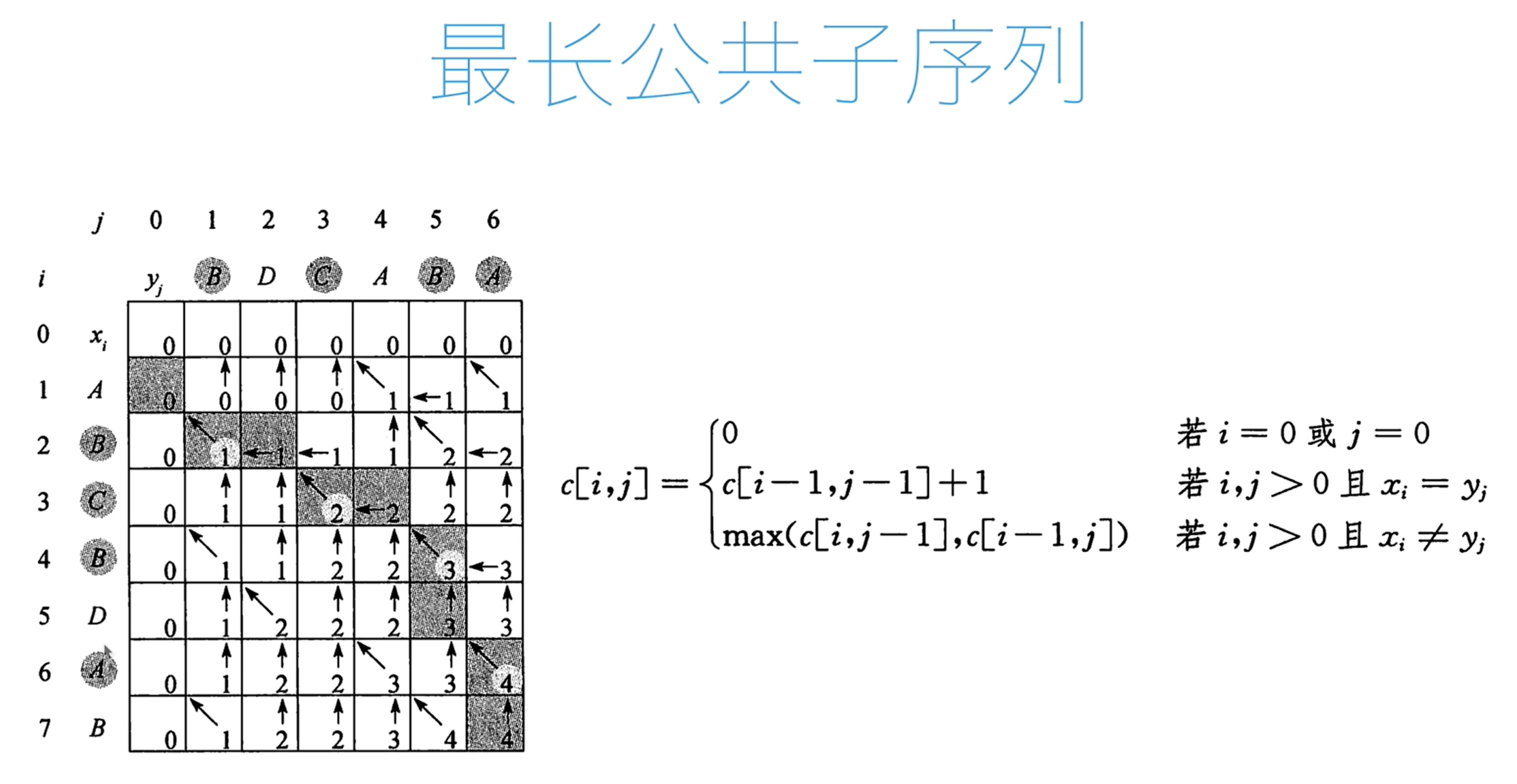
动态规划--最长公共子序列( LCS 问题)
# -*- coding: utf-8 -*-
# 最长公共子序列的长度
def lcs_length(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]: # i j 位置上的字符匹配的时候,来自于左上方+1
c[i][j] = c[i - 1][j - 1] + 1
else:
c[i][j] = max(c[i - 1][j], c[i][j - 1])
for _ in c:
print(_)
return c[m][n]
print("==========================最长公共子序列的长度==========================")
print(f'最长公共子序列的长度为:{lcs_length("ABCBDAB", "BDCABA")}')
def lcs(x, y):
m = len(x)
n = len(y)
c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
b = [[0 for _ in range(n + 1)] for _ in range(m + 1)] # 1 左上方 2 上方 3 左方
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i - 1] == y[j - 1]: # i j 位置上的字符匹配的时候,来自于左上方+1
c[i][j] = c[i - 1][j - 1] + 1
b[i][j] = 1
elif c[i - 1][j] > c[i][j - 1]: # 来自于上方
c[i][j] = c[i - 1][j]
b[i][j] = 2
else:
c[i][j] = c[i][j - 1]
b[i][j] = 3
return c[m][n], b
def lcs_trackback(x, y):
c, b = lcs(x, y)
for _ in b:
print(_)
i = len(x)
j = len(y)
res = []
while i > 0 and j > 0:
if b[i][j] == 1: # 来自左上方=>匹配
res.append(x[i - 1])
i -= 1
j -= 1
elif b[i][j] == 2: # 来自于上方=>不匹配
i -= 1
else: # ==3 来自于左方=>不匹配
j -= 1
return "".join(reversed(res))
print("===============================最长公共子序列===============================")
print(lcs_trackback("ABCBDAB", "BDCABA"))
本文作者:zylyehuo
本文链接:https://www.cnblogs.com/zylyehuo/p/17643050.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。






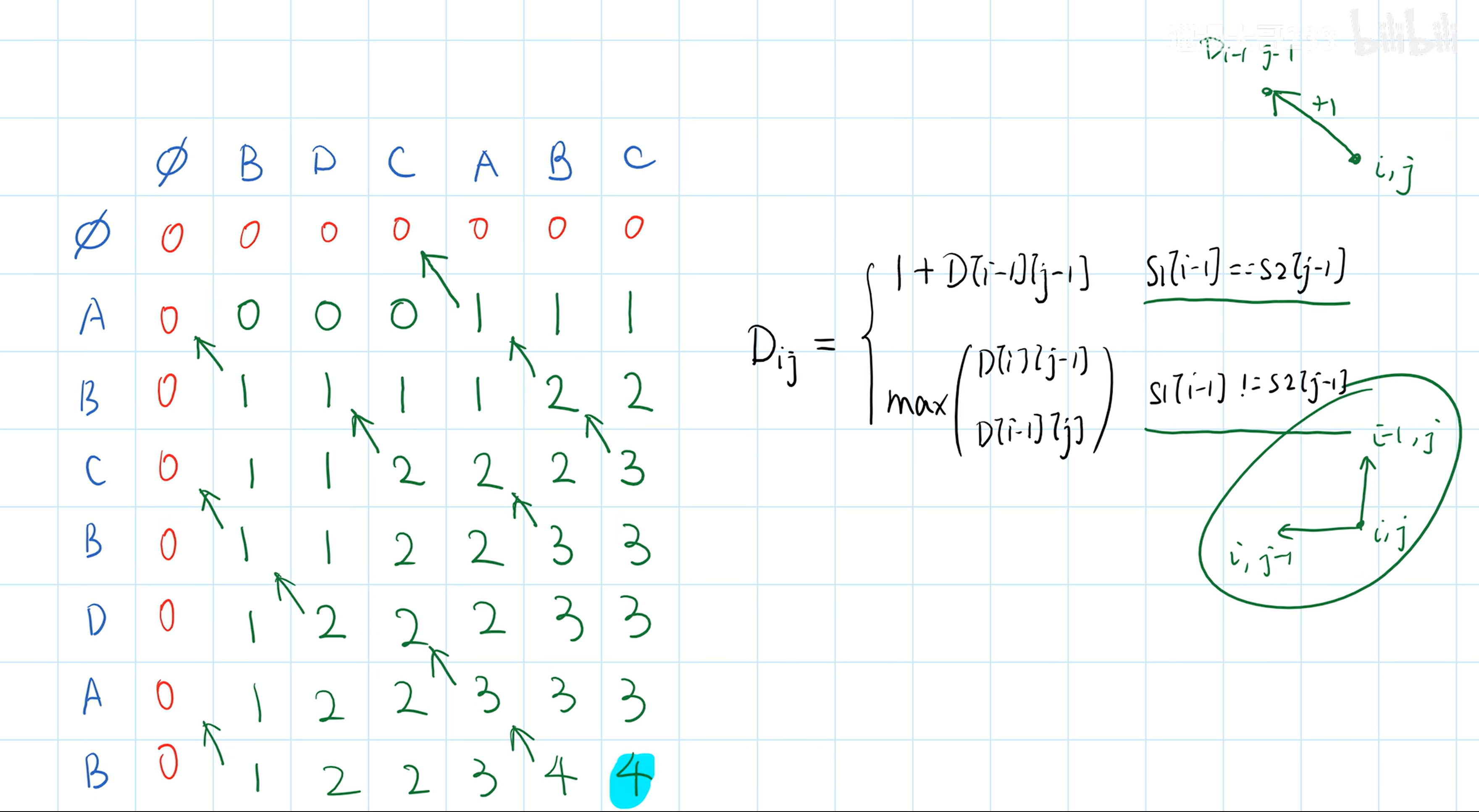




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步