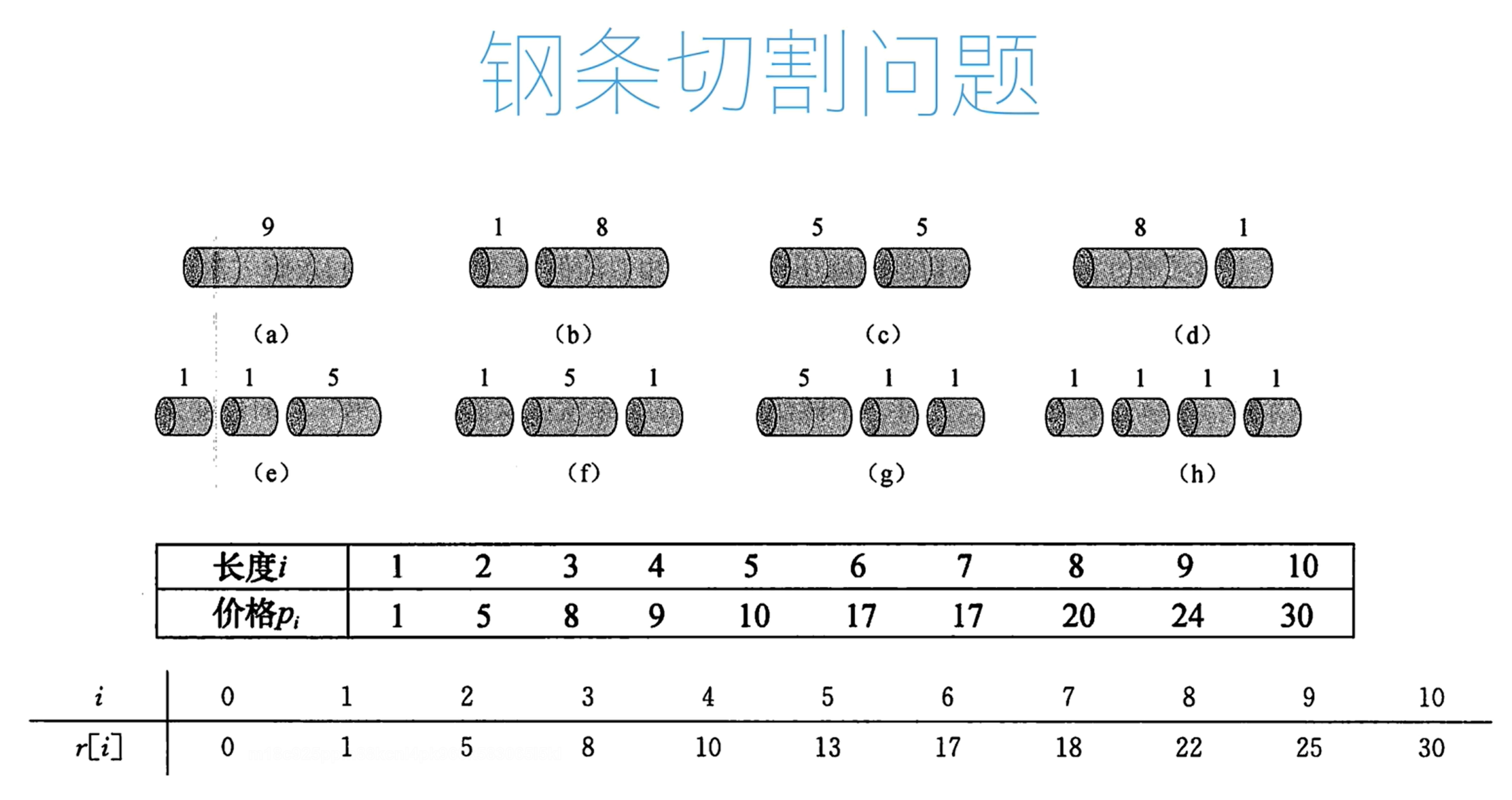
动态规划--钢条切割问题

博客地址：https://www.cnblogs.com/zylyehuo/

• 
• 
• 
• 
• 
• 
• 
• 
• 

# -*- coding: utf-8 -*-

import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2 - t1), end='--------------------')
        return result

    return wrapper


p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]


# p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

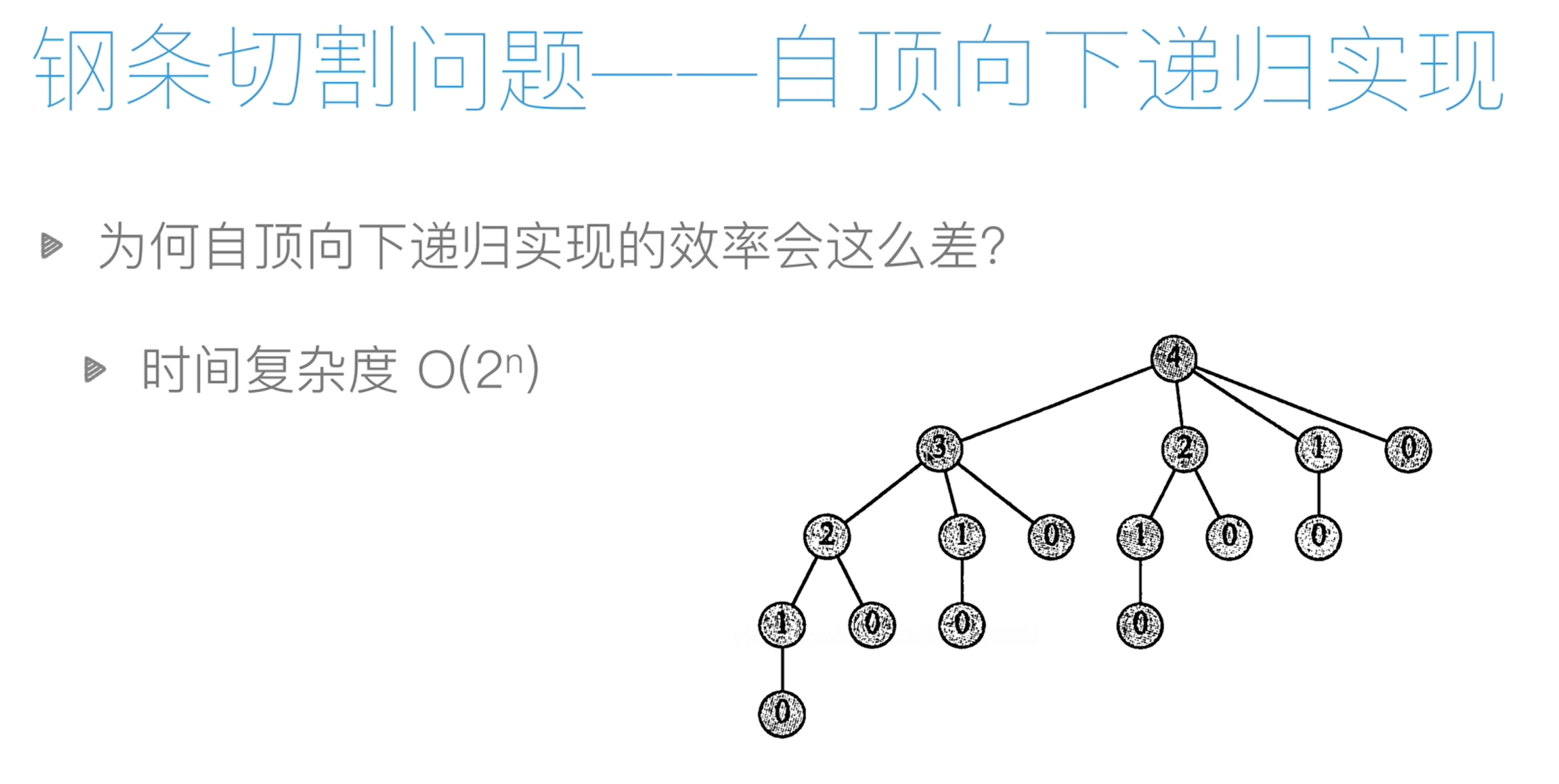
# 递归--计算效率低
def cut_rod_recurision_1(p, n):
    if n == 0:
        return 0
    else:
        res = p[n]
        for i in range(1, n):
            res = max(res, cut_rod_recurision_1(p, i) + cut_rod_recurision_1(p, n - i))
        return res


@cal_time
def c1(p, n):
    return cut_rod_recurision_1(p, n)


def cut_rod_recurision_2(p, n):
    if n == 0:
        return 0
    else:
        res = 0
        for i in range(1, n + 1):
            res = max(res, p[i] + cut_rod_recurision_2(p, n - i))
        return res


@cal_time
def c2(p, n):
    return cut_rod_recurision_2(p, n)


print(c1(p, 15))
print(c2(p, 15))


# 自底向上实现
@cal_time
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n + 1):
        res = 0
        for j in range(1, i + 1):
            res = max(res, p[j] + r[i - j])
        r.append(res)
    return r[n]


print(cut_rod_dp(p, 15))


# 重构解
def cut_rod_extend(p, n):
    r = [0]
    s = [0]
    for i in range(1, n + 1):
        res_r = 0  # 价格的最大值
        res_s = 0  # 价格最大值对应方案的左边不切割部分的长度
        for j in range(1, i + 1):
            if p[j] + r[i - j] > res_r:
                res_r = p[j] + r[i - j]
                res_s = j
        r.append(res_r)
        s.append(res_s)
    return r[n], s


print("=================================重构解=================================")
r, s = cut_rod_extend(p, 20)
print(s)


# 切割方案
def cut_rod_solution(p, n):
    r, s = cut_rod_extend(p, n)
    ans = []
    while n > 0:
        ans.append(s[n])
        n -= s[n]
    return ans


print("================================按如下切割===============================")
print(cut_rod_solution(p, 20))