第三十一节,目标检测算法之 Faster R-CNN算法详解
Ren, Shaoqing, et al. “Faster R-CNN: Towards real-time object detection with region proposal networks.” Advances in Neural Information Processing Systems. 2015.
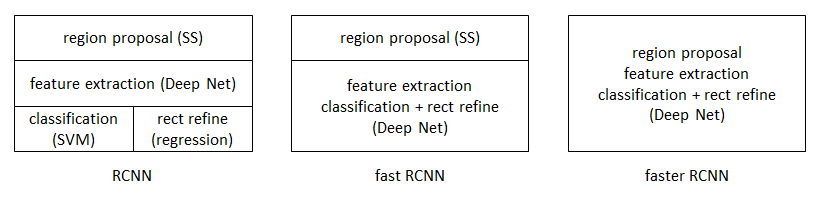
本文是继RCNN[1],fast RCNN[2]之后,目标检测界的领军人物Ross Girshick团队在2015年的又一力作。简单网络目标检测速度达到17fps,在PASCAL VOC上准确率为59.9%;复杂网络达到5fps,准确率78.8%。
作者在github上给出了基于matlab和python的源码。
上一节我们介绍到Fast R-CNN网络,Fast R-CNN看似很完美了,但是Fast R-CNN中还存在着一个优点尴尬的问题,它需要先使用Selective Search提取框,这个方法比较慢,有时,检测一张图片,大部分时间不是花费在计算神经网络分类上,而是花在Selective Search提取框上!在Fast R-CNN升级版Faster R-CNN中,使用RPN(Region Proposal Network)网络取代了Selective Search,不仅速度得到了大大提高,而且还获得了更加精确的结果。
一 Faster R-CNN思路
从R-CNN到Fast R-CNN,再到本文的Faster R-CNN,目标检测的四个基本步骤(候选区域生成,特征提取,分类,位置精修)终于被统一到一个深度网络框架之内。所有计算没有重复,完全在GPU中完成,大大提高了运行速度。
Faster R-CNN可以简单地看做“区域生成网络(RPN)+Fast RCNN“的系统,用区域生成网络代替Fast R-CNN中的Selective Search方法,网络结构如下图。本篇论文着重解决了这个系统中的三个问题:
- 如何设计区域生成网络
- 如何训练区域生成网络
- 如何让区域生成网络和Fast R-CNN网络共享特征提取网络
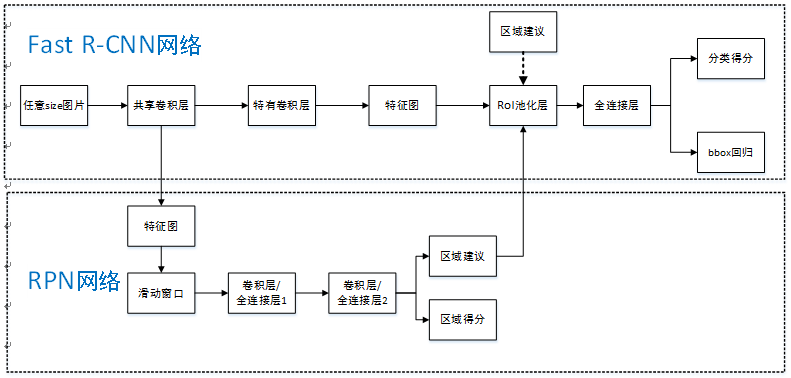
步骤如下:
- 首先向CNN网络【ZF或VGG-16】输入任意大小图片$M\times{N}$;
-
经过CNN网络前向传播至最后共享的卷积层,一方面得到供RPN网络输入的特征图,另一方面继续前向传播至特有卷积层,产生更高维特征图;
- 供RPN网络输入的特征图经过RPN网络得到区域建议和区域得分,并对区域得分采用非极大值抑制【阈值为0.7】,输出其Top-N【文中为300】得分的区域建议给RoI池化层;
- 第2步得到的高维特征图和第3步输出的区域建议同时输入RoI池化层,提取对应区域建议的特征;
- 第4步得到的区域建议特征通过全连接层后,输出该区域的分类得分以及回归后的bounding-box。
二 RPN详解
基本设想是:在提取好的特征图上,对所有可能的候选框进行判别。由于后续还有位置精修步骤,所以候选框实际比较稀疏。
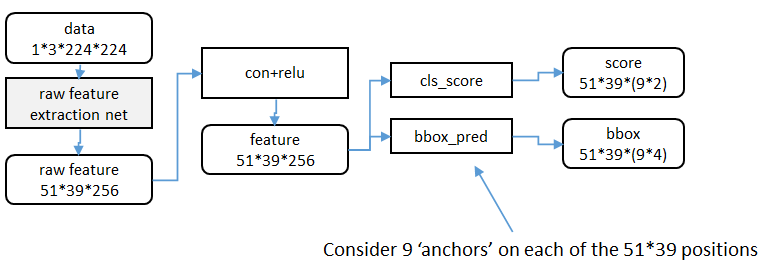
1、特征提取
RPN还是需要使用一个CNN网络对原始图片提取特征。为了方便读者理解,不妨设这个前置的CNN提取的特征为$51\times{39}\times{256}$,即高为51,宽为39,通道数为256.对这个卷积特征再进行一次卷积计算,保持宽、高、通道数不变,再次得到一个$51\times{39}\times{256}$的特征。
为了方便叙述,先来定义一个“位置”的概念:对于一个$51\times{39}\times{256}$的卷积特征,称它一共有$51\times{39}$个"位置"。让新的卷积特征的每一个"位置"都"负责”原图中对应位置的9种尺寸框的检测,检测的目标是判断框中是否存在一个物体,因此共用$51\times{39}\times{9}$个“框”。在Faster R-CNN原论文中,将这些框都统一称为"anchor"。
2、候选区域(anchor)
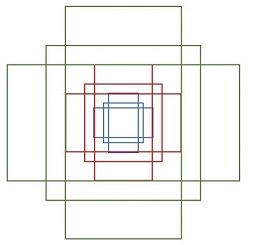
特征可以看做一个尺度$51\times{39}$的256通道图像,对于该图像的每一个位置,考虑9个可能的候选窗口:三种面积分别是$128\times{128}$,$256\times{256}$,$512\times{512}$,每种面积又分成3种长宽比,分别是2:1,1:2,1:1 。这些候选窗口称为anchors。做着就是通过这些anchors引入了检测中常用到的多尺度方法(检测各种大小的目标),下图示出$51\times{39}$个anchor中心,以及9种anchor示例。
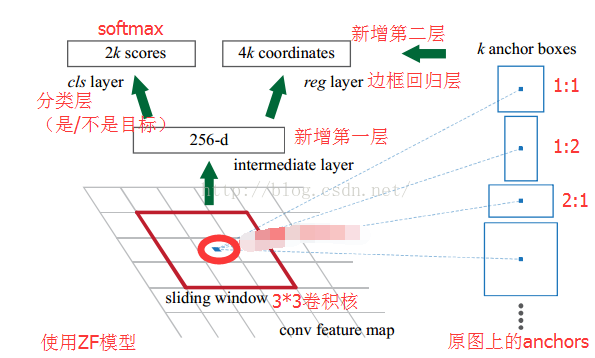
对于这$51\times{39}$个位置和$51\times{39}\times{9}$个anchor,下图展示了接下来每个位置的计算步骤:
- 设$k$为单个位置对应的anchor的个数,此时$k=9$,通过增加一个$3\times{3}$滑动窗口操作以及两个卷积层完成区域建议功能;
- 第一个卷积层将特征图每个滑窗位置编码成一个特征向量,第二个卷积层对应每个滑窗位置输出$k$个区域得分,表示该位置的anchor为物体的概率,这部分总输出长度为$2\times{k}$(一个anchor对应两个输出:是物体的概率+不是物体的概率)和k个回归后的区域建议(框回归),一个anchor对应4个框回归参数,因此框回归部分的总输出的长度为$4\times{k}$,并对得分区域进行非极大值抑制后输出得分Top-N(文中为300)区域,告诉检测网络应该注意哪些区域,本质上实现了Selective Search、EdgeBoxes等方法的功能。
3、框回归
如图绿色表示的是飞机的实际框标签(ground truth),红色的表示的其中一个候选区域(foreground anchor),即被分类器识别为飞机的区域,但是由于红色区域定位不准确,这张图相当于没有正确检测出飞机,所以我们希望采用一种方法对红色的框进行微调,使得候选区域和实际框更加接近:

对于目标框一般使用四维向量来表示$(x,y,w,h)$,分别表示目标框的中心点坐标、宽、高,我们使用$A$表示原始的foreground anchor,使用$G$表示目标的ground truth,我们的目标是寻找一种关系,使得输入原始的Anchor $A$经过映射到一个和真实框$G$更接近的回归窗口$G'$,即:
- 给定:$A=(A_x,A_y,A_w,A_h)$,$G=(G_x,G_y,G_w,G_h)$;
- 寻找一种变换$F$,使得$F(A_x,A_y,A_w,A_h)=(G_x',G_y',G_w',G_h')$,其中$(G_x,G_y,G_w,G_h)≈(G_x',G_y',G_w',G_h')$;

那么如何去计算$F$呢?这里我们可以通过平移和缩放实现$F(A)=G'$:
- 平移:
$$G_x'=A_x + A_w\cdot d_x(A)$$
$$G_y'=A_y + A_h\cdot d_y(A)$$
- 缩放:
$$G_w'=A_w\cdot exp(d_w(A))$$
$$G_h'=A_h\cdot exp(d_h(A))$$
上面公式中,我们需要学习四个参数,分别是$d_x(A),d_y(A),d_w(A),d_h(A)$,其中$(A_w\cdot d_x(A),A_w\cdot d_y(A))$表示的两个框中心距离的偏移量。当输入的anchor A与G相差较小时,可以认为这种变换是一种线性变换, 那么就可以用线性回归来建模对目标框进行微调(注意,只有当anchors A和G比较接近时,才能使用线性回归模型,否则就是复杂的非线性问题了)。
接下来就是如何通过线性回归获得$d_x(A),d_y(A),d_w(A),d_h(A)$。线性回归就是给定输入的特征向量$X$,学习一组参数$W$,使得线性回归的输出$WX$和真实值$Y$的差很小。对于该问题,输入$X$是特征图,我们使用$\phi$表示,同时训练时还需要A到G变换的真实参数值:$(t_x,t_y,t_w,t_h)$;输出是$d_x(A),d_y(A),d_w(A),d_h(A)$,那么目标函数可以表示为:$$d_*(A)=w_*^T\cdot \phi(A)$$
其中$\phi(A)$是对应anchor的特征图组成的特征向量,$w$是需要学习的参数,$d(A)$是得到预测值,(*表示$x,y,w,h$,也就是每一个变换对应一个上述目标函数),为了让预测值$d_x(A),d_y(A),d_w(A),d_h(A)$和真实值差距$t_x,t_y,t_w,t_h$最小,代价函数如下:
$$loss=\sum\limits_{i=1}^{N}(t_*^i - \hat{w}_*^T\cdot \phi(A^i))^2$$
函数优化目标为:
$$w_*=\mathop{\arg\min}_{\hat{w}_*} \sum\limits_{i=1}^{N}(t_*^i - \hat{w}_*^T\cdot \phi(A^i))^2+\lambda \|{\hat{w*}}\|2$$
需要说明,只有在G和A比较接近时,才可近似认为上述线性变换成立,下面对于原文中,A与G之间的平移参数$(t_x,t_y)$和尺度因子$(t_w,t_h)$为:
$$t_x=(G_x-A_x)/A_w$$
$$t_y=(G_y-A_y)/A_h$$
$$t_w=log(G_w/A_w)$$
$$t_h=log(G_h/A_h)$$
对于训练bouding box regression网络回归分支,输入是特征图$\phi$,监督信号是A到G的变换参数$(t_x,t_y,t_w,t_h)$,即训练的目标是:输入$\phi$的情况下使网络输出与监督信号尽可能接近。那么bouding box regression工作时,再输入$\phi$时,回归网络分支的输出就是每个anchor的平移参数和变换尺度$(t_x,t_y,t_w,t_h)$,显然即可用来修正anchor位置了。
4、候选框修正
在得到每一个候选区域anchor A的修正参数$(d_x(A),d_y(A),d_w(A),d_h(A))$之后,我们就可以计算出精确的anchor,然后按照物体的区域得分从大到小对得到的anchor排序,然后提出一些宽或者高很小的anchor(获取其它过滤条件),再经过非极大值抑制抑制,取前Top-N的anchors,然后作为proposals(候选框)输出,送入到RoI Pooling层。
三 RoI Pooling层
RoI Pooling层负责收集所有的候选框,并计算每一个候选框的特征图,然后送入后续网络,从Faster RCNN的结构图我们可以看到RoI Pooling层有两个输入:
- 原始的特征图;
- RPN网络输出的候选框;
1、为何使用RoI Pooling
先来看一个问题:对于传统的CNN(如AlexNet,VGG),当网络训练好后输入的图像尺寸必须是固定值,同时网络输出也是固定的大小。如果输入图像大小不定,这个问题就变得比较麻烦。有2种解决办法:
- 从图像中crop一部分传入网络;
- 将图像warp成需要的大小后传入网络;

两种办法的示意图如上图,可以看到无论采取那种办法都不好,要么crop后破坏了图像的完整结构,要么warp破坏了图像原始形状信息。
回忆RPN网络生成的proposals的方法:对foreground
anchors进行bounding box
regression,那么这样获得的proposals也是大小形状各不相同,即也存在上述问题。所以Faster R-CNN中提出了RoI
Pooling解决这个问题。不过RoI Pooling是从Spatial Pyramid Pooling发展而来,有兴趣的读者可以自行查阅相关论文。
2、RoI Pooling原理
我们把每一个候选框的特征图水平和垂直分为pooled_w(文章中为7)和pooled_h(7)份,对每一份进行最大池化处理,这样处理后,即使大小不一样的候选区,输出大小都一样,实现了固定长度的输出:
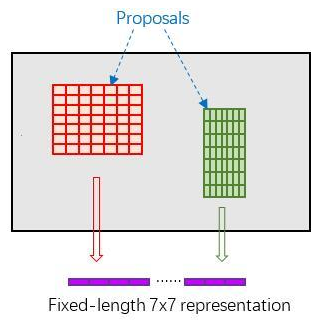
然后我们把Top-N个固定输出($7\times{7}=49$)连接起来,组成特征向量,大小为$Top-N\times{49}$,这里可以把Top-N看做样本数,49看做每一个样本的特征维数,送入全连接层。
四 分类和框回归
通过RoI Pooling层我们已经得到所有候选区组成的特征向量,然后送入全连接层和softmax计算每个候选框具体属于哪个类别,输出类别的得分;同时再次利用框回归获得每个候选区相对实际位置的偏移量预测值,用于对候选框进行修正,得到更精确的目标检测框。
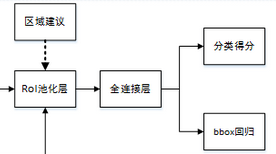
这里我们来看看全连接层,由于全连接层的参数$w$和$b$大小都是固定大小的,假设大小为$49\times26$,那么输入向量的维度就要为$Top-N\times{49}$,所以这就说明了RoI Pooling的重要性。
五 训练
Faster R-CNN使用RPN生成候选框后,剩下的网络结构和Fast R-CNN中的结构一模一样。在训练过程中,需要训练两个网络,一个是RPN网络,一个是在得到框之后使用的分类网络。通常的做法是交替训练,即在一个batch内,先训练RPN网络一次,再训练分类网络一次。关于训练的详细流程可以参考一文读懂Faster RCNN。
参考文章:
[4]Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks
[5]基于深度学习的目标检测技术演进:R-CNN、Fast R-CNN、Faster R-CNN(强烈推荐)
[7]RCNN,Fast RCNN,Faster RCNN 总结
[9]一文读懂Faster RCNN(这位大佬讲的很细、相信这看了这篇文章,对Faster RCNN的实现细节你会有了更深的了解)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号