第十八节,自编码网络介绍及代码实现
人们平时看一幅图片时,并不是像计算机那样逐个像素去读,一般是扫一眼物体,大致能得到需要的信息,如形状、颜色和特征等,那么怎么让机器也具有这项能力呢?这里就介绍一下自编码网络。
自编码网络是非监督学习领域中的一种,可以自动从无标注的数据中学习特征,是一种以重构输入信息为目标的神经网络,它可以给出比原始数据更好的特征描述,具有较强的特征学习能力,在深度学习中常用自编码网络生成的特征来取代原始数据,以取得更好的效果。
那么这种网络有什么实际应用呢?自编码器是当前深度学习研究的热点之一,有很多重要的应用领域,这里仅举一个有趣的例子,大家还记得前一段时间百度推出的上传你的照片,系统帮你找到与你像的明星吗?其实这个功能就可以用自编码器来实现,首先,我们将已经训练好的自编码器的输入层和中间层组成的网络拿出来,将所有明星的脸进行压缩,得到一个人脸向量,保存起来,然后,当普通用户上传了自己的照片后,系统将用户照片输入自编码器的输入层,从中间层得到该用户的人脸向量,最后拿这个用户的人脸向量与明星们的人脸向量进行比较,找出向量距离最近的一个或几个明星,将明星的照片作为与用户最像的明星照片,返回给用户。由于百度这项服务推出的时间较早,应该不是基于自动编码器实现的,但是使用自动编码器,完全可以实现这个功能。
上一节我们介绍到了受限玻尔兹曼机模型,也可以重构输入信息,提取特征信息。他们具体有什么差异呢?下面我将会详细介绍一下自编码器,以及和受限玻尔兹曼机的区别。
一 自编码网络和受限玻尔兹曼机
自编码器(AE)和受限玻尔兹曼机(RBM)是在深度神经网络领域广泛使用的两种常见的基础性结构。它们都可以作为无监督学习的框架,通过最小化重构误差,提取系统的重要特征;更重要的是,通过多层的堆叠和逐层的预训练,层叠式自动编码器和深度信念网络都可以在后续监督学习的过程中,帮助整个神经网络更好更快地收敛到最小值点。
1.最简单的自编码器网络
什么是自编码?所谓自编码就是自己给自己编码,再简单点就是令输出等于输入自己。以一个简单三层网络为例如下: 、

自编码器通过隐藏层对输入进行了压缩,并在输出层中解压缩,整个过程肯定会丢失信息,但是通过训练我们能够使丢失的信息尽量减少,最大化的保留其主要特征。
这里我们假设输出等于输入来训练这个网络参数(可能训练好的网络参数不可能让输出百分百等于输入,至少会非常接近吧)。那么这个网络在输入确定了以后(这时输出也就确定了吧),唯一需要确定的就是隐含层的个数了吧,以上述这个图为例,我们可以看到,网络的输入与输出都是一个6维的向量,而隐含层是3个,也就是3维。
那么这种自编码有什么意义呢?它又有什么用呢?可以看到,自编码可以使得网络通过学习转化成一组另外的量,这组量又可以通过解码恢复成原始的量,这样一来一回的过程看上去没什么用,但是你把分开着来看就会发现很有用,原始的量可以通过编码映射成另一组量吧,这一组量既然可以通过译码恢复成原始的量,说明了什么?中间这一层的输出是不是就是原始输入的另外一种表达了?是的。这就好比一个人,你看得到时候直接看就是一个人,当你看不到人的时候,比如说你听到了他的名字,你也知道这个名字表示的就是这个人。所以这个名字就是这个人的另一种条件下的新特征,而往往这种新特征更能去分这个人是谁。
好了再看看上面这个图,输入6维,隐含层以后变成了3维,输出还是6维,我们单看到隐含层发现了什么?是不是输入从6维降到了3维?但是这3为在某种意义上还是原始数据的典型特征吧,言外之意是不是相当于降维了。如果知道主成分分析法(PCA)的人应该了解,PCA方法其实就是实现数据降维的,如果自编码网络激活函数不使用Sigmoid函数,而使用心形函数,那么便是PCA模型了。在这里我们通过这种自编码,规定隐含层神经元的个数以后,通过自编码的训练,让网络的输出尽可能的等于输入,待自编码完成后,那么输入通过隐含层的输出就相当于降维了吧(前提是隐含层的神经元个数要小于输入维数,这样才叫降维,否则的话叫升维),说到升维,了解PCA的朋友你们有没有试过PCA升维呢?PCA能不能升维呢?哈哈,貌似不能,没试过。但是理论上是可以的。那么升维相当于将信息复杂化,这种操作有没有用呢?可能还是有用的吧,了解SVM的朋友知道,SVM里面就有将非线性数据通过升维以后可以在线性范围内可分,那么这里的升维是不是也能将原始非线性的数据变到线性呢?可以去试试看,应该有那么个意思。
好了说了这么多,我们还是来看降维的情况,通过自编码实现数据的降维思想最初是2006年深度学习领域大牛Hinton想出来的,并且发表在顶级期刊Science上,文章的出处在这里:“reducing the dimensionality of data with neural networks”
该篇经典之作也被视为深度学习的开山之作,自此以后深度学习火了起来,并且逐渐打败传统模式识别领域的浅层学习算法。我们知道,机器学习或者模式识别,对数据的主要工作在做什么?无非提取数据的主要特征,那么以前可能所有的特征要么是人为设计出来,要么是浅层学习出来的,像PCA,他们虽然一定程度上有用,但是相对于深度学习这种将数据的各个层次的特征都学习出来了的相比自然弱了不少,这也是深度学习的最强大之处。
2.受限玻尔兹曼机
上一节已经详细介绍了RBM网络,这里不再具体介绍,只做一个简单的总结。
RBM是实现深度学习的另一种神经网络结构。RBM的基本功能与AE类似,RBM同样也可以对数据进行编码,多层RBM也可以用于对神经网络进行初始化的预训练。
RBM是一种基于能量的神经网络模型,它具有深刻的统计物理背景。RBM训练的目标即为让RBM网络表示的概率分布与输入样本的分布尽可能地接近,这一训练同样是无监督式的。在实践中,常常用对比散度(CD)的方法来对网络进行训练,CD算法较好地解决了RBM学习效率的问题。在用CD算法开始进行训练时,所有可见神经元的初始状态被设置成某一个训练样本,将这些初始参数代入到激活函数中,可以算出所有隐藏层神经元的状态,进而用激活函数产生可见层的一个重构。通过比照重构结果和初始状态,RBM的各参数可以得以更新,从这一点来看,用CD算法对RBM进行训练与AE的训练是非常相似的。近年来,CD算法有许多改进,例如:持续性对比散度(PCD)和快速持续性对比散度(FPCD)等;而在训练RBM时,也可以利用非CD式的算法,例如比率匹配等。
3.自编码器与受限玻尔兹曼机的区别
AE与RBM两种算法之间也有着重要的区别,这种区别的核心在于:AE希望通过非线性变换找到输入数据的特征表示,它是某种确定论性的模型;而RBM的训练则是围绕概率分布进行的,它通过输入数据的概率分布(能量函数)来提取高层表示,它是某种概率论性的模型。从结构的角度看,AE的编码器和解码器都可以是多层的神经网络,而通常我们所说的RBM只是一种两层的神经网络。在训练AE的过程中,当输出的结果可以完全重构输入数据时,损失函数 L 被最小化,而损失函数常常被定义为输出与输出之间的某种偏差(例如均方差等),它的偏导数便于直接计算,因此可以用传统的BP算法进行优化。RBM最显著的特点在于其用物理学中的能量概念重新描述了概率分布,它的学习算法基于最大似然,网络能量函数的偏导不能直接计算,而需要用统计的方法进行估计,因此需要用CD算法等来对 RBM 进行训练。
二 自编码网络的代码实现
1.提取图片的特征,并利用特征还原图片
通过构建一个量程的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 ,下面以MNIST数据集为例,将其像素点组成的数据(28x28)从784维降维到256,然后再降到128,最后再以同样的方式经过256,最终还原到原来的图片。
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt from tensorflow.examples.tutorials.mnist import input_data def two_layer_auto_encoder(): ''' 通过构建一个量程的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 下面以MNIST数据集为例,将其像素点组成的数据(28x28)从784维降维到256,然后再降到128,最后再以同样的 方式经过256,最终还原到原来的图片。 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 #输入节点 n_hidden_1 = 256 #第一次256个节点 n_hidden_2 = 128 #第二层128个节点 batch_size = 256 #小批量大小 training_epochs = 20 #迭代轮数 display_epoch = 5 #迭代2轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 input_x = tf.placeholder(dtype=tf.float32,shape=[None,n_input]) #输入 input_y = input_x #输出 #学习参数 weights = { 'encoder_h1':tf.Variable(tf.random_normal(shape=[n_input,n_hidden_1])), 'encoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_hidden_2])), 'decoder_h1':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_1])), 'decoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_input])) } biases = { 'encoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'encoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'decoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'decoder_b2':tf.Variable(tf.random_normal(shape=[n_input])) } #编码 当我们对最终提取的特征节点采用sigmoid函数时,就相当于对输入限制或者缩放,使其位于[0,1]范围中 encoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(input_x,weights['encoder_h1']),biases['encoder_b1'])) encoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h1,weights['encoder_h2']),biases['encoder_b2'])) #解码 decoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h2,weights['decoder_h1']),biases['decoder_b1'])) pred = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h1,weights['decoder_h2']),biases['decoder_b2'])) ''' 设置代价函数 ''' #对所有元素求和求平均 cost = tf.reduce_mean((input_y - pred)**2) ''' 求解,开始训练 ''' #train = tf.train.RMSPropOptimizer(learning_rate).minimize(cost) train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:mnist.test.images[:show_num]}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(mnist.test.images[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show()
下图为程序运行的结果,图片分为上下两行,第一行显示的是输入图片,第二行显示的是重构图片。

在上面的代码中,我们使用的激活函数为sigmoid激活函数,输出范围是[0,1],当我们对最终提取的特征节点采用激励函数时,竟相当于对输入限制或缩放,使其位于[0,1]范围中。有一些数据集,比如MNIST,能方便地将输出缩放到[0,1]中,但是很难满足对输入值的要求。例如,PCA白化处理的输入并不满足[0,1]的范围要求,页不清楚是否有最好的办法将数据缩放到特定范围中。
如果利用一个恒等式来作为激励函数,就可以很好的解决这个问题,即f(z)=z作为激励函数。
由多个带有sigmois激活函数的隐藏层以及一个线性输出层构成的自编码器,称为线性解码器。
2.提取图片的二维特征,并利用二维特征还原图片
通过构建一个2维的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 ,这里使用4层逐渐压缩将785维度分别压缩成256,64,16,2这4个特征向量,最后再还原。并且在这里我们使用了线性解码器,在编码的最后一层,没有进行sigmoid变化,这是因为生成的二维特征数据其特征已经标的极为主要,所有我们希望让它传到解码器中,少一些变化可以最大化地保存原有的主要特征,当然这一切是通过分析之后实际测试得来的结果。
def four_layer_auto_encoder(): ''' 通过构建一个2维的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 这里使用4层逐渐压缩将785维度分别压缩成256,64,16,2这4个特征向量,最后再还原 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 #输入节点 n_hidden_1 = 256 n_hidden_2 = 64 n_hidden_3 = 16 n_hidden_4 = 2 batch_size = 256 #小批量大小 training_epochs = 20 #迭代轮数 display_epoch = 5 #迭代1轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 input_x = tf.placeholder(dtype=tf.float32,shape=[None,n_input]) #输入 input_y = input_x #输出 #学习参数 weights = { 'encoder_h1':tf.Variable(tf.random_normal(shape=[n_input,n_hidden_1])), 'encoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_hidden_2])), 'encoder_h3':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_3])), 'encoder_h4':tf.Variable(tf.random_normal(shape=[n_hidden_3,n_hidden_4])), 'decoder_h1':tf.Variable(tf.random_normal(shape=[n_hidden_4,n_hidden_3])), 'decoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_3,n_hidden_2])), 'decoder_h3':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_1])), 'decoder_h4':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_input])) } biases = { 'encoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'encoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'encoder_b3':tf.Variable(tf.random_normal(shape=[n_hidden_3])), 'encoder_b4':tf.Variable(tf.random_normal(shape=[n_hidden_4])), 'decoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_3])), 'decoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'decoder_b3':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'decoder_b4':tf.Variable(tf.random_normal(shape=[n_input])) } #编码 encoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(input_x,weights['encoder_h1']),biases['encoder_b1'])) encoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h1,weights['encoder_h2']),biases['encoder_b2'])) encoder_h3 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h2,weights['encoder_h3']),biases['encoder_b3'])) #在编码的最后一层,没有进行sigmoid变化,这是因为生成的二维特征数据其特征已经标的极为主要,所有我们希望让它 #传到解码器中,少一些变化可以最大化地保存原有的主要特征 #encoder_h4 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h3,weights['encoder_h4']),biases['encoder_b4'])) encoder_h4 = tf.add(tf.matmul(encoder_h3,weights['encoder_h4']),biases['encoder_b4']) #解码 decoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h4,weights['decoder_h1']),biases['decoder_b1'])) decoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h1,weights['decoder_h2']),biases['decoder_b2'])) decoder_h3 = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h2,weights['decoder_h3']),biases['decoder_b3'])) pred = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h3,weights['decoder_h4']),biases['decoder_b4'])) ''' 设置代价函数 ''' #求平均 cost = tf.reduce_mean((input_y - pred)**2) ''' 求解,开始训练 ''' train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:mnist.test.images[:show_num]}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(mnist.test.images[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show() ''' 显示二维的特征数据 有点聚类的感觉,一般来说通过自编码网络将数据降维之后更有利于进行分类处理 ''' plt.figure(figsize=(10,8)) #将onehot转为一维编码 labels = [np.argmax(y) for y in mnist.test.labels] encoder_result = sess.run(encoder_h4,feed_dict={input_x:mnist.test.images}) plt.scatter(encoder_result[:,0],encoder_result[:,1],c=labels) plt.colorbar() plt.show()
下图为线性解码器运行后的结果:
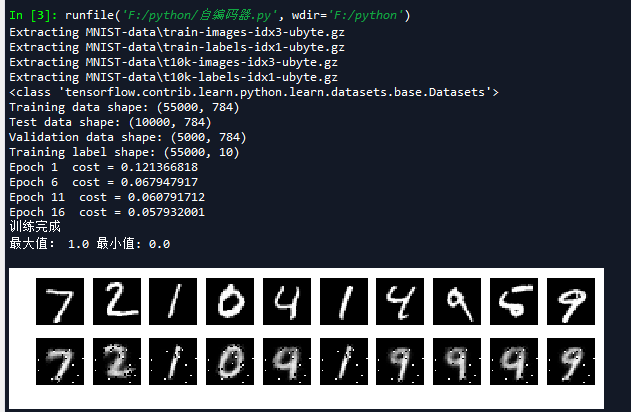
然后我们再把编码的最后一层,改为simoid函数测试,结果如下:
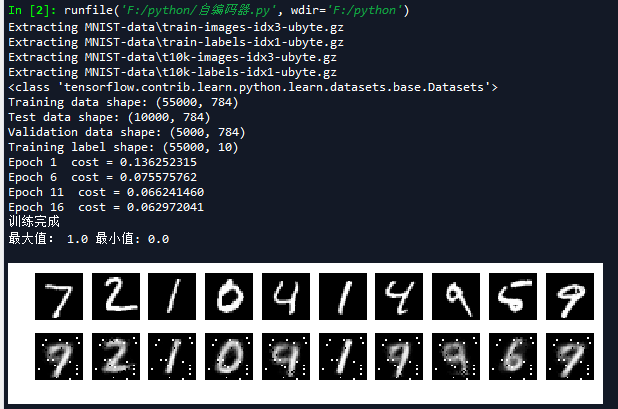
对比上面两张图,我们可以看到重构出来的效果并不理想,和实际输入有误差,可能是因为层数变多,存在现实的梯度问题,我们可以通过调参来尝试一下会有什么效果。我们对比这两张图的第二行,我们会发现第一张图的噪声比较少,这说明线性编码器效果更好。
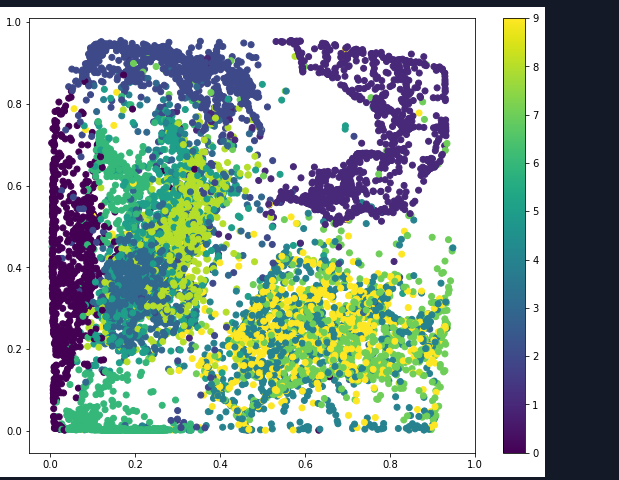
我们再来看一下这张图,是不是有一种聚类的感觉,一般来说通过自编码网络将数据降维之后更有利于进行分类处理。
3.实现卷积网络的自编码
自编码结构不尽只用在全网络连接上,还可以用在卷积网络上。我们在原有代码的基础上把全连接改成卷积,把解码改成反卷积,反池化,代码如下:(GPU环境才可以运行)
def max_pool_with_argmax(net,stride): ''' 重定义一个最大池化函数,返回最大池化结果以及每个最大值的位置(是个索引,形状和池化结果一致) args: net:输入数据 形状为[batch,in_height,in_width,in_channels] stride:步长,是一个int32类型,注意在最大池化操作中我们设置窗口大小和步长大小是一样的 ''' #使用mask保存每个最大值的位置 这个函数只支持GPU操作 _, mask = tf.nn.max_pool_with_argmax( net,ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1],padding='SAME') #将反向传播的mask梯度计算停止 mask = tf.stop_gradient(mask) #计算最大池化操作 net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1],strides=[1, stride, stride, 1], padding='SAME') #将池化结果和mask返回 return net,mask def un_max_pool(net,mask,stride): ''' 定义一个反最大池化的函数,找到mask最大的索引,将max的值填到指定位置 args: net:最大池化后的输出,形状为[batch, height, width, in_channels] mask:位置索引组数组,形状和net一样 stride:步长,是一个int32类型,这里就是max_pool_with_argmax传入的stride参数 ''' ksize = [1, stride, stride, 1] input_shape = net.get_shape().as_list() # calculation new shape output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3]) # calculation indices for batch, height, width and feature maps one_like_mask = tf.ones_like(mask) batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1]) b = one_like_mask * batch_range y = mask // (output_shape[2] * output_shape[3]) x = mask % (output_shape[2] * output_shape[3]) // output_shape[3] feature_range = tf.range(output_shape[3], dtype=tf.int64) f = one_like_mask * feature_range # transpose indices & reshape update values to one dimension updates_size = tf.size(net) indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size])) values = tf.reshape(net, [updates_size]) ret = tf.scatter_nd(indices, values, output_shape) return ret def cnn_auto_encoder(): tf.reset_default_graph() ''' 通过构建一个卷积网络的自编码,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 batch_size = 256 #小批量大小 n_conv_1 = 16 #第一层16个ch n_conv_2 = 32 #第二层32个ch training_epochs = 8 #迭代轮数 display_epoch = 5 #迭代2轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 使用反卷积的时候,这个形状中不能带有None,不然会报错 input_x = tf.placeholder(dtype=tf.float32,shape=[batch_size,n_input]) #输入 #input_y = input_x #输出 #学习参数 weights = { 'encoder_conv1': tf.Variable(tf.truncated_normal([5, 5, 1, n_conv_1],stddev=0.1)), 'encoder_conv2': tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2],stddev=0.1)), 'decoder_conv1': tf.Variable(tf.random_normal([5, 5, 1, n_conv_1],stddev=0.1)), 'decoder_conv2': tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2],stddev=0.1)) } biases = { 'encoder_conv1': tf.Variable(tf.zeros([n_conv_1])), 'encoder_conv2': tf.Variable(tf.zeros([n_conv_2])), 'decoder_conv1': tf.Variable(tf.zeros([n_conv_1])), 'decoder_conv2': tf.Variable(tf.zeros([n_conv_2])), } image_x = tf.reshape(input_x,[-1,28,28,1]) #编码 当我们对最终提取的特征节点采用sigmoid函数时,就相当于对输入限制或者缩放,使其位于[0,1]范围中 encoder_conv1 = tf.nn.relu(tf.nn.conv2d(image_x, weights['encoder_conv1'],strides=[1,1,1,1],padding = 'SAME') + biases['encoder_conv1']) print('encoder_conv1:',encoder_conv1.shape) encoder_conv2 = tf.nn.relu(tf.nn.conv2d(encoder_conv1, weights['encoder_conv2'],strides=[1,1,1,1],padding = 'SAME') + biases['encoder_conv2']) print('encoder_conv2:',encoder_conv2.shape) encoder_pool2, mask = max_pool_with_argmax(encoder_conv2, 2) #池化 print('encoder_pool2:',encoder_pool2.shape) #解码 decoder_upool = un_max_pool(encoder_pool2,mask,2) #反池化 decoder_conv1 = tf.nn.conv2d_transpose(decoder_upool - biases['decoder_conv2'], weights['decoder_conv2'],encoder_conv1.shape,strides=[1,1,1,1],padding='SAME') pred = tf.nn.conv2d_transpose(decoder_conv1 - biases['decoder_conv1'], weights['decoder_conv1'], image_x.shape,strides=[1,1,1,1],padding='SAME') print('pred:',pred.shape) ''' 设置代价函数 ''' #求平均 cost = tf.reduce_mean((image_x - pred)**2) ''' 求解,开始训练 ''' #train = tf.train.RMSPropOptimizer(learning_rate).minimize(cost) train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:batch_x}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(batch_x[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show()
完整代码如下:

# -*- coding: utf-8 -*- """ Created on Tue May 22 15:30:46 2018 @author: zy """ ''' 利用自编码网络提取图片的特征,并利用特征还原图片 ''' import tensorflow as tf import numpy as np import matplotlib.pyplot as plt from tensorflow.examples.tutorials.mnist import input_data def two_layer_auto_encoder(): ''' 通过构建一个量程的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 下面以MNIST数据集为例,将其像素点组成的数据(28x28)从784维降维到256,然后再降到128,最后再以同样的 方式经过128,再经过256,最终还原到原来的图片。 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 #输入节点 n_hidden_1 = 256 #第一次256个节点 n_hidden_2 = 128 #第二层128个节点 batch_size = 256 #小批量大小 training_epochs = 20 #迭代轮数 display_epoch = 5 #迭代2轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 input_x = tf.placeholder(dtype=tf.float32,shape=[None,n_input]) #输入 input_y = input_x #输出 #学习参数 weights = { 'encoder_h1':tf.Variable(tf.random_normal(shape=[n_input,n_hidden_1])), 'encoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_hidden_2])), 'decoder_h1':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_1])), 'decoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_input])) } biases = { 'encoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'encoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'decoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'decoder_b2':tf.Variable(tf.random_normal(shape=[n_input])) } #编码 当我们对最终提取的特征节点采用sigmoid函数时,就相当于对输入限制或者缩放,使其位于[0,1]范围中 encoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(input_x,weights['encoder_h1']),biases['encoder_b1'])) encoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h1,weights['encoder_h2']),biases['encoder_b2'])) #解码 decoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h2,weights['decoder_h1']),biases['decoder_b1'])) pred = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h1,weights['decoder_h2']),biases['decoder_b2'])) ''' 设置代价函数 ''' #对一维的ndarray求平均 cost = tf.reduce_mean((input_y - pred)**2) ''' 求解,开始训练 ''' #train = tf.train.RMSPropOptimizer(learning_rate).minimize(cost) train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:mnist.test.images[:show_num]}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(mnist.test.images[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show() def four_layer_auto_encoder(): ''' 通过构建一个2维的自编码网络,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 这里使用4层逐渐压缩将785维度分别压缩成256,64,16,2这4个特征向量,最后再还原 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 #输入节点 n_hidden_1 = 256 n_hidden_2 = 64 n_hidden_3 = 16 n_hidden_4 = 2 batch_size = 256 #小批量大小 training_epochs = 20 #迭代轮数 display_epoch = 5 #迭代1轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 input_x = tf.placeholder(dtype=tf.float32,shape=[None,n_input]) #输入 input_y = input_x #输出 #学习参数 weights = { 'encoder_h1':tf.Variable(tf.random_normal(shape=[n_input,n_hidden_1])), 'encoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_hidden_2])), 'encoder_h3':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_3])), 'encoder_h4':tf.Variable(tf.random_normal(shape=[n_hidden_3,n_hidden_4])), 'decoder_h1':tf.Variable(tf.random_normal(shape=[n_hidden_4,n_hidden_3])), 'decoder_h2':tf.Variable(tf.random_normal(shape=[n_hidden_3,n_hidden_2])), 'decoder_h3':tf.Variable(tf.random_normal(shape=[n_hidden_2,n_hidden_1])), 'decoder_h4':tf.Variable(tf.random_normal(shape=[n_hidden_1,n_input])) } biases = { 'encoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'encoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'encoder_b3':tf.Variable(tf.random_normal(shape=[n_hidden_3])), 'encoder_b4':tf.Variable(tf.random_normal(shape=[n_hidden_4])), 'decoder_b1':tf.Variable(tf.random_normal(shape=[n_hidden_3])), 'decoder_b2':tf.Variable(tf.random_normal(shape=[n_hidden_2])), 'decoder_b3':tf.Variable(tf.random_normal(shape=[n_hidden_1])), 'decoder_b4':tf.Variable(tf.random_normal(shape=[n_input])) } #编码 encoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(input_x,weights['encoder_h1']),biases['encoder_b1'])) encoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h1,weights['encoder_h2']),biases['encoder_b2'])) encoder_h3 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h2,weights['encoder_h3']),biases['encoder_b3'])) #在编码的最后一层,没有进行sigmoid变化,这是因为生成的二维特征数据其特征已经标的极为主要,所有我们希望让它 #传到解码器中,少一些变化可以最大化地保存原有的主要特征 #encoder_h4 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h3,weights['encoder_h4']),biases['encoder_b4'])) encoder_h4 = tf.add(tf.matmul(encoder_h3,weights['encoder_h4']),biases['encoder_b4']) #解码 decoder_h1 = tf.nn.sigmoid(tf.add(tf.matmul(encoder_h4,weights['decoder_h1']),biases['decoder_b1'])) decoder_h2 = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h1,weights['decoder_h2']),biases['decoder_b2'])) decoder_h3 = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h2,weights['decoder_h3']),biases['decoder_b3'])) pred = tf.nn.sigmoid(tf.add(tf.matmul(decoder_h3,weights['decoder_h4']),biases['decoder_b4'])) ''' 设置代价函数 ''' #对一维的ndarray求平均 cost = tf.reduce_mean((input_y - pred)**2) ''' 求解,开始训练 ''' train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:mnist.test.images[:show_num]}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(mnist.test.images[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show() ''' 显示二维的特征数据 有点聚类的感觉,一般来说通过自编码网络将数据降维之后更有利于进行分类处理 ''' plt.figure(figsize=(10,8)) #将onehot转为一维编码 labels = [np.argmax(y) for y in mnist.test.labels] encoder_result = sess.run(encoder_h4,feed_dict={input_x:mnist.test.images}) plt.scatter(encoder_result[:,0],encoder_result[:,1],c=labels) plt.colorbar() plt.show() def max_pool_with_argmax(net,stride): ''' 重定义一个最大池化函数,返回最大池化结果以及每个最大值的位置(是个索引,形状和池化结果一致) args: net:输入数据 形状为[batch,in_height,in_width,in_channels] stride:步长,是一个int32类型,注意在最大池化操作中我们设置窗口大小和步长大小是一样的 ''' #使用mask保存每个最大值的位置 这个函数只支持GPU操作 _, mask = tf.nn.max_pool_with_argmax( net,ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1],padding='SAME') #将反向传播的mask梯度计算停止 mask = tf.stop_gradient(mask) #计算最大池化操作 net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1],strides=[1, stride, stride, 1], padding='SAME') #将池化结果和mask返回 return net,mask def un_max_pool(net,mask,stride): ''' 定义一个反最大池化的函数,找到mask最大的索引,将max的值填到指定位置 args: net:最大池化后的输出,形状为[batch, height, width, in_channels] mask:位置索引组数组,形状和net一样 stride:步长,是一个int32类型,这里就是max_pool_with_argmax传入的stride参数 ''' ksize = [1, stride, stride, 1] input_shape = net.get_shape().as_list() # calculation new shape output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3]) # calculation indices for batch, height, width and feature maps one_like_mask = tf.ones_like(mask) batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1]) b = one_like_mask * batch_range y = mask // (output_shape[2] * output_shape[3]) x = mask % (output_shape[2] * output_shape[3]) // output_shape[3] feature_range = tf.range(output_shape[3], dtype=tf.int64) f = one_like_mask * feature_range # transpose indices & reshape update values to one dimension updates_size = tf.size(net) indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size])) values = tf.reshape(net, [updates_size]) ret = tf.scatter_nd(indices, values, output_shape) return ret def cnn_auto_encoder(): tf.reset_default_graph() ''' 通过构建一个卷积网络的自编码,将MNIST数据集的数据特征提取处来,并通过这些特征重建一个MNIST数据集 ''' ''' 导入MNIST数据集 ''' #mnist是一个轻量级的类,它以numpy数组的形式存储着训练,校验,测试数据集 one_hot表示输出二值化后的10维 mnist = input_data.read_data_sets('MNIST-data',one_hot=True) print(type(mnist)) #<class 'tensorflow.contrib.learn.python.learn.datasets.base.Datasets'> print('Training data shape:',mnist.train.images.shape) #Training data shape: (55000, 784) print('Test data shape:',mnist.test.images.shape) #Test data shape: (10000, 784) print('Validation data shape:',mnist.validation.images.shape) #Validation data shape: (5000, 784) print('Training label shape:',mnist.train.labels.shape) #Training label shape: (55000, 10) ''' 定义参数,以及网络结构 ''' n_input = 784 batch_size = 256 #小批量大小 n_conv_1 = 16 #第一层16个ch n_conv_2 = 32 #第二层32个ch training_epochs = 8 #迭代轮数 display_epoch = 5 #迭代2轮输出5次信息 learning_rate = 1e-2 #学习率 show_num = 10 #显示的图片个数 #定义占位符 使用反卷积的时候,这个形状中不能带有None,不然会报错 input_x = tf.placeholder(dtype=tf.float32,shape=[batch_size,n_input]) #输入 #input_y = input_x #输出 #学习参数 weights = { 'encoder_conv1': tf.Variable(tf.truncated_normal([5, 5, 1, n_conv_1],stddev=0.1)), 'encoder_conv2': tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2],stddev=0.1)), 'decoder_conv1': tf.Variable(tf.random_normal([5, 5, 1, n_conv_1],stddev=0.1)), 'decoder_conv2': tf.Variable(tf.random_normal([3, 3, n_conv_1, n_conv_2],stddev=0.1)) } biases = { 'encoder_conv1': tf.Variable(tf.zeros([n_conv_1])), 'encoder_conv2': tf.Variable(tf.zeros([n_conv_2])), 'decoder_conv1': tf.Variable(tf.zeros([n_conv_1])), 'decoder_conv2': tf.Variable(tf.zeros([n_conv_2])), } image_x = tf.reshape(input_x,[-1,28,28,1]) #编码 当我们对最终提取的特征节点采用sigmoid函数时,就相当于对输入限制或者缩放,使其位于[0,1]范围中 encoder_conv1 = tf.nn.relu(tf.nn.conv2d(image_x, weights['encoder_conv1'],strides=[1,1,1,1],padding = 'SAME') + biases['encoder_conv1']) print('encoder_conv1:',encoder_conv1.shape) encoder_conv2 = tf.nn.relu(tf.nn.conv2d(encoder_conv1, weights['encoder_conv2'],strides=[1,1,1,1],padding = 'SAME') + biases['encoder_conv2']) print('encoder_conv2:',encoder_conv2.shape) encoder_pool2, mask = max_pool_with_argmax(encoder_conv2, 2) #池化 print('encoder_pool2:',encoder_pool2.shape) #解码 decoder_upool = un_max_pool(encoder_pool2,mask,2) #反池化 decoder_conv1 = tf.nn.conv2d_transpose(decoder_upool - biases['decoder_conv2'], weights['decoder_conv2'],encoder_conv1.shape,strides=[1,1,1,1],padding='SAME') pred = tf.nn.conv2d_transpose(decoder_conv1 - biases['decoder_conv1'], weights['decoder_conv1'], image_x.shape,strides=[1,1,1,1],padding='SAME') print('pred:',pred.shape) ''' 设置代价函数 ''' #对一维的ndarray求平均 cost = tf.reduce_mean((image_x - pred)**2) ''' 求解,开始训练 ''' #train = tf.train.RMSPropOptimizer(learning_rate).minimize(cost) train = tf.train.AdamOptimizer(learning_rate).minimize(cost) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) #计算一轮跌倒多少次 num_batch = int(np.ceil(mnist.train.num_examples/batch_size)) #迭代 for epoch in range(training_epochs): sum_loss = 0.0 for i in range(num_batch): batch_x,batch_y = mnist.train.next_batch(batch_size) _,loss = sess.run([train,cost],feed_dict={input_x:batch_x}) sum_loss += loss #打印信息 if epoch % display_epoch == 0: print('Epoch {} cost = {:.9f}'.format(epoch+1,sum_loss/num_batch)) print('训练完成') #输出图像数据最大值和最小值 print('最大值:',np.max(mnist.train.images[0]),'最小值:',np.min(mnist.train.images[0])) ''' 可视化结果 ''' reconstruction = sess.run(pred,feed_dict = {input_x:batch_x}) plt.figure(figsize=(1.0*show_num,1*2)) for i in range(show_num): plt.subplot(2,show_num,i+1) plt.imshow(np.reshape(batch_x[i],(28,28)),cmap='gray') plt.axis('off') plt.subplot(2,show_num,i+show_num+1) plt.imshow(np.reshape(reconstruction[i],(28,28)),cmap='gray') plt.axis('off') plt.show() if __name__ == '__main__': #two_layer_auto_encoder() four_layer_auto_encoder() #cnn_auto_encoder()
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号