第十七节，受限玻尔兹曼机网络及代码实现

"受限波尔兹曼"这名字听起来就霸气，算法如其名，也挺难的。之所以难，是因为我们大部分人都没学过概率图模型，其实RBM是条件随机场的变体，所以如果学习这个算法，建议先把CRF给熟悉了，那么学起来就会轻松很多。受限玻尔兹曼机是由Geoff Hinton发明，是一种用于降维、分类、回归、协同过滤、特征学习和主题搭建的算法。RBM网络作为一种无监督学习的方法，其目的是尽可能地表达输入数据的的规则和特征。

一 网络结构

我们首先介绍一下受限玻尔兹曼机这类神经网络，因为它相对简单具有重要的历史意义。下文将以示意图和通俗的语言解释其运作原理。

RBM是有两个层的浅层神经网络，它是组成深度置信网络的基础部件。RBM的第一个层称为可见层，又称输入层，由显元 (visible units) 组成，用于输入训练数据。第二个层是隐藏层，相应地，由隐元 (hidden units) 组成，用作特征检测器 (feature detectors)。

上图中每个圆圈都是一个与神经元相似的单元，称为节点，运算在节点中进行。一个层中的节点与另一层中的所有节点分别连接，但与同一层中的其它节点并不相连。

也就是说，层的内部不存在通信－这就是受限玻尔兹曼机被称为受限的原因。每个节点对输入进行处理和运算，判定是否继续传输输入的数据，而这种判定一开始是随机的。(“随机”（stochastic）一词在此处指与输入相乘的初始系数是随机生成的。)

每个可见节点负责处理网络需要学习的数据集中一个项目的一种低层次特征。举例来说，如果处理的是一个灰度图像的数据集，则每个可见节点将接收一张图像中每个像素的像素值。（MNIST图像有784个像素，所以处理这类图像的神经网络的一个可见层必须有784个输入节点。）

接着来看单个像素值x如何通过这一双层网络。在隐藏层的节点1中x与一个权重相乘，再与所谓的偏差相加。这两步运算的结果输入激活函数，得到节点的输出，即输入为x时通过节点的信号强度。

输出a = 激活函数f((权重w * 输入x) + 偏差b )

 

下面来看一个隐藏节点如何整合多项输入。每个x分别与各自的权重相乘，乘积之和再与偏差相加，其结果同样经过激活函数运算得到节点的输出值。

 

由于每个可见节点的输入都被传递至所有的隐藏节点，所以也可将RBM定义为一种对称二分图。

对称指每个可见节点都与所有的隐藏节点相连接（见下图）。二分指有两个部分或层，而这里的图是指代节点网络的数学名词。

在每个隐藏节点中，每一个输入x都会与其相对应的权重w相乘。也就是说，每个输入x会对应三个权重，因此总共有12个权重（4个输入节点 x 3个隐藏节点）。两层之间的权重始终都是一个行数等于输入节点数、列数等于输出节点数的矩阵。

每个隐藏节点会接收四个与对应权重相乘后的输入值。这些乘积之和与一个偏差值相加（至少能强制让一部分节点激活），其结果再经过激活运算得到每个隐藏节点的输出a。

 

如果这两个层属于一个深度神经网络，那么第一隐藏层的输出会成为第二隐藏层的输入，随后再通过任意数量的隐藏层，直至到达最终的分类层。（简单的前馈动作仅能让RBM节点实现自动编码器的功能。）

二 重构

我们重点关注RBM如何在无监督情况系学习重构数据，在可见层和第一个隐藏层之间进行多次正向和反向传播，而无需加大网络的深度。

在重构阶段，第一个隐藏层的激活值成为反向传播中的输入。这些输入值与同样的权重相乘，每两个相连的节点之间各有一个权重，就像正向传播中输入x的加权运算一样。这些乘积的和再与每个可见层的偏差相加，所得结果就是重构值，亦即原始输入的近似值，这一过程可以用下图来表示：

由于RBM的权重初始化是随机的，重构值与原始输入之间的差别通常很大。可以将r值与输入之差视为重构误差，此误差值随后经由反向传播来修正RBM的权重，如此不断的反复，直至误差达到最小。

• RBM在正向传递中使用输入值来预测节点的激活值，即输入为x时输出a的概率：p(a|x:w)。
• 但在反向传播时，激活值成为输入，而输出的是对于原始数据的重构值，或者说猜测值，此时RBM则是在尝试估计激活值为a时输入为x的概率，激活值得加权系数与正向传播中的权重相同。第二个阶段可以表示为：p(x|a:w)。

上述两种预测值相结合，可以得到输入x和激活值a的联合概率分布，即p(x,a)。

重构与回归，分类运算不同，回归运算根据需要输入值估计一个连续值，分类运算时猜测应当为一个特定的输入样例添加哪种具体的标签。而重构则是在猜测原始输入的概率分布，即同时预测许多不同的点的值，这被称为生成学习，必须和分类器所进行的判别学习区分开来，后者是将输入值映射至标签，用直线将数据划分为不同的组。

试想输入数据和重构数据是形状不同的常态曲线，两者仅有部分重叠。RBM用Kullback Leibler来衡量预测的概率分布与输入值的基准分布之间的距离。

KL散度衡量两条曲线下方不重叠(即散度)的面积，而RBM的优化算法会尝试将这些离散部分的面积最小化，使共用权重在与第一层的激活值相乘后，可以得到与原始输入高度近似的结果。下图左半边是一组原始输入的概率分布曲线ρ，与之并列的是重构值的概率分布曲线q，右半边的图则显示了两条曲线之间的差异。

 

 RBM根据权重产生的误差反复调整权重，以此学习估计原始数据的近似值。可以说权重会慢慢开始反映出输入的结构，而这种结构被编码为第一个隐藏层的激活值。整个学习过程看上去像是两条概率分布曲线在逐步重合。

 

三 使用 RBM 的过程 

假设我们现在已经得到一个训练好的 RBM，每个隐藏节点与输入节点间的权重用矩阵W表示，且： 

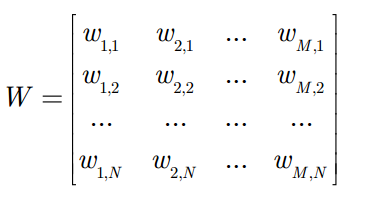
其中W_ij代表从第i个输入节点到第j个隐藏节点的权重，M代表输入节点的个数，N代表隐藏节点的个数。那么，当我们把一条新来的数据赋给 (clamp to) 输入层后，RBM 将会依照权值W来决定开启或关闭隐藏节点。具体的操作如下： 

• 首先，将每个隐藏节点的激励值 (activation) 计算出来： 

 注意，这里用到了前面提到的神经元之间的条件独立性。 

• 然后，将每个隐藏节点的激励值都用 S 形函数进行标准化，变成它们处于开启状 (用 1 表示) 的概率值： 

此处的 S 形函数我们采用的是 Logistic 函数： 

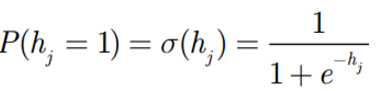
• 至此，每个隐藏节点h_j开启的概率被计算出来了。其处于关闭状态 (用 0 表示) 的概率自然也就是 

• 通常RBM中的神经元都是二值化的，也就是说只有开启和不开启两种状态，也就是0或者1。那么到底这个元开启还是关闭，我们需要将开启的概率与一个从 0, 1 均匀分布中抽取的随机值 

 进行如下比较 

然后开启或关闭相应的隐藏节点。

给定隐藏层，计算输入层的方法是一样的。 

 

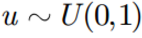
四 训练 RBM

 RBM 的训练过程，实际上是求出一个最能产生训练样本的概率分布。也就是说，要求一个分布，在这个分布里，训练样本的概率最大。由于这个分布的决定性因素在于权值W ，所以我们训练 RBM 的目标就是寻找最佳的权值。为了保持读者的兴趣，这里我们不给出最大化对数似然函数的推导过程，直接说明如何训练 RBM。 

G. Hinton 提出了名为对比散度 (Contrastive Divergence) 的学习算法。下面我们来详述它的具体过程。 我们沿用前文的符号记法。 

 

如此训练之后的 RBM 就能较为准确地提取输入层的特征，或者根据隐藏层所代表的特征还原输入层了。 

如果想了解反向传播梯度的具体计算过程请参考文章：简单易学的机器学习算法——受限玻尔兹曼机RBM

 

五 实例代码

 我们以MNIST数据集为例，进行训练，并打印出部分原始图像，以及重构后的图像，进行对比。程序中为了计算方便，我们的权重形状选择的是NxM，也就是之前假设的W的转置。

# -*- coding: utf-8 -*-
"""
Created on Sat May 19 09:30:02 2018

@author: zy
"""

'''
受限的玻尔兹曼机:https://blog.csdn.net/zc02051126/article/details/9668439
'''
import matplotlib.pylab as plt
import numpy as np
import random


class RBM(object):
    '''
    定义一个RBM网络类
    '''
    
    def __init__(self,n_visible,n_hidden,momentum=0.5,learning_rate=0.1,max_epoch=50,batch_size=128,penalty=0,weight=None,v_bias=None,h_bias=None):
        '''
        RBM网络初始化
        
        使用动量的随机梯度下降法训练网络
        args:
            n_visible:可见层节点个数
            n_hidden：隐藏层节点个数
            momentum:动量参数 一般取值0.5,0.9,0.99  当取值0.9时，对应着最大速度1/(1-0.9)倍于梯度下降算法
            learning_rate：学习率
            max_epoch：最大训练轮数
            batch_size：小批量大小        
            penalty：规范化 权重衰减系数  一般设置为1e-4  默认不使用
            weight：权重初始化参数，默认是n_hidden x n_visible
            v_bias:可见层偏置初始化 默认是 [n_visible]
            h_bias:隐藏层偏置初始化 默认是 [n_hidden]
        '''
        #私有变量初始化
        self.n_visible = n_visible
        self.n_hidden = n_hidden
        self.max_epoch = max_epoch
        self.batch_size = batch_size
        self.penalty = penalty        
        self.learning_rate = learning_rate
        self.momentum = momentum
        
        
        if weight is None:
            self.weight = np.random.random((self.n_hidden,self.n_visible))*0.1        #用于生成一个0到0.1的随机符点数
        else:
            self.weight = weight
        if v_bias is None:
            self.v_bias = np.zeros(self.n_visible)                                    #可见层偏置
        else:
            self.v_bias = v_bias
        if h_bias is None:
            self.h_bias = np.zeros(self.n_hidden)                                     #隐藏层偏置
        else:
            self.h_bias = h_bias
                    
            
    def sigmoid(self,z):
        '''
        定义s型函数
        
        args:
            z：传入元素or list 、nparray
        '''
        return 1.0/(1.0+np.exp(-z))
    
    def forword(self,inpt):
        '''
        正向传播
        
        args:
            inpt : 输入数据(可见层) 大小为batch_size x n_visible
        '''
        z = np.dot(inpt,self.weight.T) + self.h_bias        #计算加权和
        return self.sigmoid(z)
    
    def backward(self,inpt):
        '''
        反向重构
        
        args:
            inpt : 输入数据(隐藏层) 大小为batch_size x n_hidden
        '''
        z = np.dot(inpt,self.weight) + self.v_bias    #计算加权个
        return self.sigmoid(z) 
    
    def batch(self):
        '''
        把数据集打乱，按照batch_size分组
        '''
        #获取样本个数和特征个数
        m,n = self.input_x.shape               
        
        #生成打乱的随机数
        per = list(range(m))
        random.shuffle(per)
        
        per = [per[k:k+self.batch_size] for k in range(0,m,self.batch_size)]
        
        batch_data = []
        for group in per:
            batch_data.append(self.input_x[group])        
        return batch_data

    
    def fit(self,input_x):
        '''
        开始训练网络
        
        args:
            input_x:输入数据集
        '''        
        self.input_x = input_x                                
                
        Winc = np.zeros_like(self.weight)
        binc = np.zeros_like(self.v_bias)
        cinc = np.zeros_like(self.h_bias)
        
        #开始每一轮训练
        for epoch in range(self.max_epoch):
              
            batch_data = self.batch()
            num_batchs = len(batch_data)
            
            #存放平均误差
            err_sum = 0.0            
            
            #随着迭代次数增加 penalty减小
            self.penalty = (1 - 0.9*epoch/self.max_epoch)*self.penalty
            
            
            #训练每一批次数据集
            for v0 in  batch_data:                     
                '''
                RBM网络计算过程
                '''                
                #前向传播  计算h0
                h0 = self.forword(v0)                
                h0_states = np.zeros_like(h0)                        
                #从 0, 1 均匀分布中抽取的随机值，尽然进行比较判断是开启一个隐藏节点，还是关闭一个隐藏节点
                h0_states[h0 > np.random.random(h0.shape)] = 1                
                #print('h0',h0.shape)              
                
                #反向重构  计算v1
                v1 = self.backward(h0_states)
                v1_states = np.zeros_like(v1)
                v1_states[v1 > np.random.random(v1.shape)] = 1
                #print('v1',v1.shape)
                
                #前向传播 计算h1
                h1 = self.forword(v1_states)
                h1_states = np.zeros_like(h1)                                        
                h1_states[h1 > np.random.random(h1.shape)] = 1
                #print('h1',h1.shape)
                
                
                '''更新参数 权重和偏置  使用栋梁的随机梯度下降法'''
                #计算batch_size个样本的梯度估计值
                dW = np.dot(h0_states.T , v0) - np.dot(h1_states.T , v1)
                #沿着axis=0进行合并
                db = np.sum(v0 - v1,axis=0).T
                dc = np.sum(h0 - h1,axis=0).T
            
                #计算速度更新
                Winc = self.momentum  * Winc + self.learning_rate * (dW  - self.penalty * self.weight)/self.batch_size 
                binc = self.momentum  * binc + self.learning_rate * db / self.batch_size
                cinc = self.momentum  * cinc + self.learning_rate * dc / self.batch_size
                
                #对于最大化对数似然函数  使用梯度下降法是加号 最小化是减号  开始更新
                self.weight = self.weight + Winc
                self.v_bias = self.v_bias + binc
                self.h_bias = self.h_bias + cinc
       
            
                
                err_sum = err_sum + np.mean(np.sum((v0 - v1)**2,axis=1))                        
                
            #计算平均误差
            err_sum = err_sum /num_batchs              
            print('Epoch {0},err_sum {1}'.format(epoch, err_sum))
            
    def predict(self,input_x):   
        '''
        预测重构值
        
        args:
            input_x：输入数据
        '''
        #前向传播  计算h0
        h0 = self.forword(input_x)                
        h0_states = np.zeros_like(h0)                        
        #从 0, 1 均匀分布中抽取的随机值，尽然进行比较判断是开启一个隐藏节点，还是关闭一个隐藏节点
        h0_states[h0 > np.random.random(h0.shape)] = 1                        
        
        #反向重构  计算v1
        v1 = self.backward(h0_states)
        return v1
    
    
    def visualize(self, input_x):  
        '''
        传入 形状为m xn的数据 即m表示图片的个数  n表示图像的像素个数
        
        其中 m = row x row
        n = s x s
        
        args:        
            input_x:形状为 m x n的数据
        '''        
        #获取输入样本的个数和特征数
        m, n = input_x.shape   
                
        #获取每张图像的宽和高 默认宽=高
        s = int(np.sqrt(n))          
                        
        #把所有图片以 row x row排列
        row = int(np.ceil(np.sqrt(m)))  
        
        #其中多出来的row + 1是用于绘制边框的 
        data = np.zeros((row*s + row + 1, row * s + row + 1)) - 1.0
        
        #图像在x轴索引
        x = 0  
        #图像在y轴索引
        y = 0  
        #遍历每一张图像
        for i in range(m):                 
            z = input_x[i]                  
            z = np.reshape(z,(s,s))
            #填充第i张图像数据                
            data[x*s + x + 1 :(x+1)*s + x + 1 , y*s + y + 1 :(y+1)*s + y + 1] = z  
            x = x + 1  
            #换行
            if(x >= row):  
                x = 0  
                y = y + 1                           
        return data  


def read_data(path):  
    '''
    加载数据集  数据按行分割，每一行表示一个样本，每个特征使用空格分割
    
    args:
        path：数据文件路径
    '''
    data = []  
    for line in open(path, 'r'):  
        ele = line.split(' ')  
        tmp = []  
        for e in ele:  
            if e != '':  
                tmp.append(float(e.strip(' ')))  
        data.append(tmp)  
    return data  


if __name__ == '__main__':  
    #加载MNIST数据集 总共有5000张图像，每张图像有784个像素点   MNIST数据集可以从网上下载
    data = read_data('data.txt')  
    data = np.array(data)  
    print(data.shape)                  #(5000, 784)    
    
    #创建RBM网络
    rbm = RBM(784, 100,max_epoch = 50,learning_rate=0.05)  
    #开始训练
    rbm.fit(data)  


    #显示64张手写数字 
    images = data[0:64]
    print(images.shape)
    a = rbm.visualize(images)
    fig = plt.figure(1,figsize=(8,8))      
    plt.imshow(a,cmap=plt.cm.gray)  
    plt.title('original data')      
      
    #显示重构的图像
    rebuild_value = rbm.predict(images)
    b = rbm.visualize(rebuild_value)  
    fig = plt.figure(2,figsize=(8,8))      
    plt.imshow(b,cmap=plt.cm.gray)  
    plt.title('rebuild data')  
      
    
    #显示权重
    w_value = rbm.weight  
    c = rbm.visualize(w_value)  
    fig = plt.figure(3,figsize=(8,8))    
    plt.imshow(c,cmap=plt.cm.gray)  
    plt.title('weight value(w)')  
    plt.show()                                      

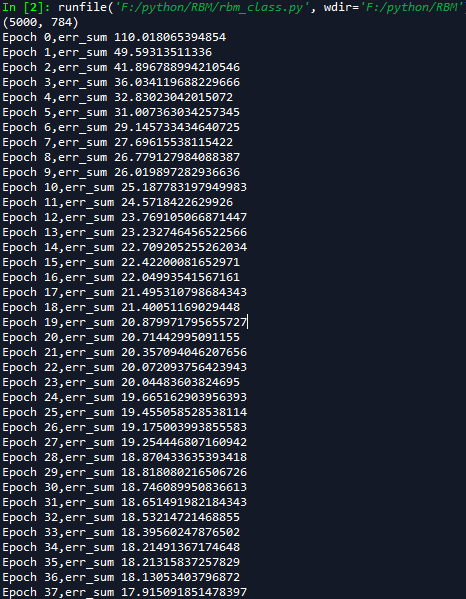
运行结果如下：

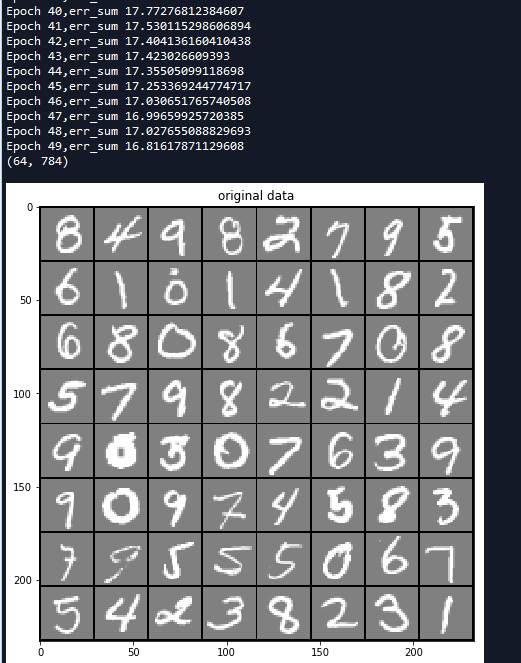
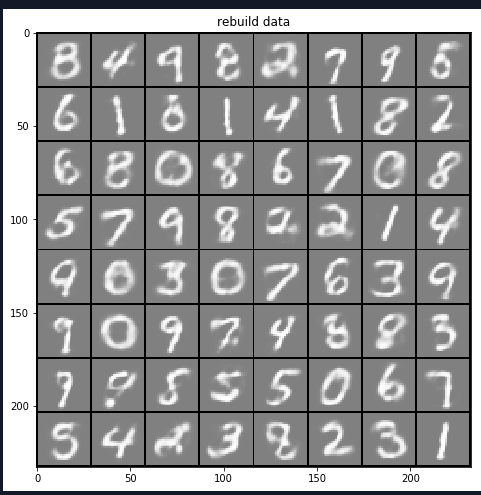
参考文献

[1] Andrew Ng机器学习笔记（三）（拓展）深度学习与受限玻尔兹曼机(推荐)

[2]受限玻尔兹曼机基础教程 

[3]深度信念网络与受限玻尔兹曼机

[4]受限玻尔兹曼机——简单证明

[5]简单易学的机器学习算法——受限玻尔兹曼机RBM

[6]受限的玻尔兹曼机

[7]受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）

[8]深度学习（八）RBM受限波尔兹曼机学习-未完待续