第十九节,使用RNN实现一个退位减法器
退位减法具有RNN的特性,即输入的两个数相减时,一旦发生退位运算,需要将中间状态保存起来,当高位的数传入时将退位标志一并传入参与计算。
我们在做减法运算时候,把减数和被减数转换为二进制然后进行运算。我们定义一个RNN网络,输入节点数为2个,依次传入减数和被减数的二进制序列值,隐藏层节点数为16个,由于二进制减法输出值为0或者1,所以输出节点数为可以设置为1个或者2个,如果设置为2个,表示看成一个二分类问题;如果设置为1个,就表示输出的值,这里我们设置输出节点数为1个,输出层使用的是S型函数。
一 定义基本函数
由于使用二进制运算,每一位的值只可能为0或者1,因此激活函数全部选择S型函数。
#规定随机数生成器的种子,可以每次得到一样的值 np.random.seed(0) ''' 一 定义基本函数 ''' def sigmoid(x): ''' 定义S型函数 args: x:输入数或list、ndarray ''' return 1/(1+np.exp(-x)) def sigmoid_output_to_derivative(output): ''' 定义sigmod的导数 args: output:sigmoid函数的输出 假设要计算x=5时,sigmoid函数的导数,此处就传入sigmoid(5) ''' return output*(1-output)
二 建立二进制映射关系
我们定义减法的最大限制在256以内,即8位数的减法,定义int与二进制之间的映射字典int2binary。
''' 二 建立二进制映射 定义的减法最大值限制在256以内,即8位二进制的减法,定义int与二进制之间的映射字典int2binary ''' #整数到其二进制表示的映射字典 int2binary = {} #二进制的位数 binary_dim = 8 #计算0-255的二进制表示 largest_number = pow(2,binary_dim) ''' 注意 np.array([range(largest_number)],dtype=np.uint8) 返回的是[[0,1,2,3...255]] 形状1x256 如果使用这个后面需要.T进行转置 np.array(range(largest_number),dtype=np.uint8) 返回的是[0,1,2,...255]形状为(256,) 尽量不使用这种形状不明确的 然后按行转为二进制 得到256x8 ''' binary = np.unpackbits( np.array(range(largest_number),dtype=np.uint8).reshape(256,1),axis=1) #建立int-二进制映射 for i in range(largest_number): #向字典中追加数据 int2binary[i] = binary[i]
三 定义参数
定义权重和偏置,这里我们为了简化运算,忽略偏置。
''' 三 定义参数 隐藏层的权重synapse_0(2x16),输出层的权重synapse_1(16x1),循环节点的权重synapse_h(16x16) 这里只设置权重 忽略偏置 ''' #参数设置 learning_rate = 0.9 #学习速率 input_dim = 2 #输入节点的个数为2,减数和被减数 hidden_dim = 16 #隐藏层节点个数 output_dim = 1 #输出节点个数 n_samples = 10000 #样本个数 #初始化网络 np.random.random生成一个[0,1)之间随机浮点数或size大小浮点数组 synapse_0 = (2*np.random.random((input_dim,hidden_dim))-1)*0.05 #-0.05~0.05之间 synapse_1 = (2*np.random.random((hidden_dim,output_dim))-1)*0.05 #-0.05~0.05之间 synapse_h = (2*np.random.random((hidden_dim,hidden_dim))-1)*0.05 #-0.05~0.05之间 #用于存放反向传播的权重梯度值 synapse_0_update = np.zeros_like(synapse_0) synapse_1_update = np.zeros_like(synapse_1) synapse_h_update = np.zeros_like(synapse_h)
四 准备样本数据
随机生成减数和被减数数据,并计算结果。这里要求被减数要大于减数。最后并把这些数转换为二进制。
''' 四 准备样本数据 ''' #建立循环生成样本数据,先生成两个数a,b,如果a小于b,就交换位置,保证被减数大 for i in range(n_samples): #生成一个数字a 被减数 范围[0,256)之间的整数 a_int = np.random.randint(largest_number) #生成一个数字b 减数,b的最大值取得是largest_number/2 b_int = np.random.randint(largest_number/2) #如果生成的b>a交换 if a_int < b_int: tmp = b_int b_int = a_int a_int = tmp #二进制编码 a = int2binary[a_int] #被减数 b = int2binary[b_int] #减数 c = int2binary[a_int - b_int] #差值
五 模型初始化
初始化神经网络的预测值为0,初始化总误差为0,定义layer_2_deltas存储反向传播过程中输出层的误差,layer_1_values存放隐藏层的输出值,由于第一个数据传入时,没有前面的隐藏层输出值来作为本次的输入,所以需要为其定义一个初始值,这里定义为0.1.
''' 五 模型初始化 ''' d = np.zeros_like(c) #存储神经网络的预测值 初始化为0 over_all_error = 0 #初始化总误差为0 layer_2_deltas = list() #存储每个时间点输出层的误差 layer_1_values = list() #存储每个时间点隐藏层的值 layer_1_values.append(np.ones(hidden_dim)*0.1) #一开始没有隐藏层(t=1),所以初始化原始值为0.1
六 正向传播
循环遍历每个二进制,从个位开始依次相减,并将中间隐藏层的输出传入下一位的计算(退位减法),把每一个时间点的误差导数都记录下来,同时统计总误差,为输出准备。
''' 六 正向传播 ''' #循环遍历每一个二进制位 for position in range(binary_dim): #生成输入和输出 从右向左,每次取两个输入数字的一个bit位 X = np.array([[a[binary_dim - position- 1],b[binary_dim - position - 1]]]) #正确答案 y = np.array([[c[binary_dim - position -1]]]).T #计算隐藏层输出 新的隐藏层 = 输入层 + 之前的隐藏层 layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h)) #将隐藏层保存下来,下个事件序列可以使用 layer_1_values.append(copy.deepcopy(layer_1)) #计算输出层 layer_2 = sigmoid(np.dot(layer_1,synapse_1)) #预测误差 layer_2_error = layer_2 - y #把每个时间点的误差导数都记录下来 layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2)) #总误差 over_all_error += np.abs(layer_2_error[0]) #记录每个预测的bit位 d[binary_dim - position - 1] = np.round(layer_2[0][0]) fuature_layer_1_delta = np.zeros(hidden_dim)
最后一行代码是为了反向传播准备的初始化。同正向传播一样,反向传播是从最后一次往前反向计算误差,对于每一个当前的计算都需要有它的下一次结果参与。反向计算从最后一次开始的,它没有后一次的输入,这里初始化为0.
七 反向训练
初始化之后,开始从高位往回训练,一次对每一位的所有层计算误差,并根据每层误差对权重求梯度,得到其调整值,最终将每一位算出的各层权重的调整值加载一块乘以学习率,来更新各层的权重,完成一次优化训练。
''' 七 反向训练 ''' for position in range(binary_dim): X = np.array([[a[position],b[position]]]) #最后一次的两个输入 layer_1 = layer_1_values[-position-1] #当前时间点的隐藏层 prev_layer_1 = layer_1_values[-position-2] #前一个时间点的隐藏层 layer_2_delta = layer_2_deltas[-position-1] #当前时间点输出导数 #通过后一个时间点的一隐藏层误差和当前时间点的输出层误差,计算当前时间点的隐藏层误差 layer_1_delta = (fuature_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T))*sigmoid_output_to_derivative(layer_1) #等完成了所有反向传播误差计算,才会更新权重矩阵,先暂时把梯度矩阵存起来 synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta) synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta) synapse_0_update += X.T.dot(layer_1_delta) fuature_layer_1_delta = layer_1_delta #完成所有反向传播之后,更新权重矩阵,并把矩阵梯度变量清0 synapse_0 -= synapse_0_update*learning_rate synapse_1 -= synapse_1_update*learning_rate synapse_h -= synapse_h_update*learning_rate synapse_0_update = 0 synapse_1_update = 0 synapse_h_update = 0
八 输出
'''
八 打印输出结果
'''
if i%800 == 0:
print('总误差:',str(over_all_error))
print('Pred:',str(d))
print('True:',str(c))
out = 0
for index,x in enumerate(reversed(d)):
out += x*pow(2,index)
print(str(a_int) + '-' + str(b_int) + '=' + str(out))
print('-------------------------------------------------')
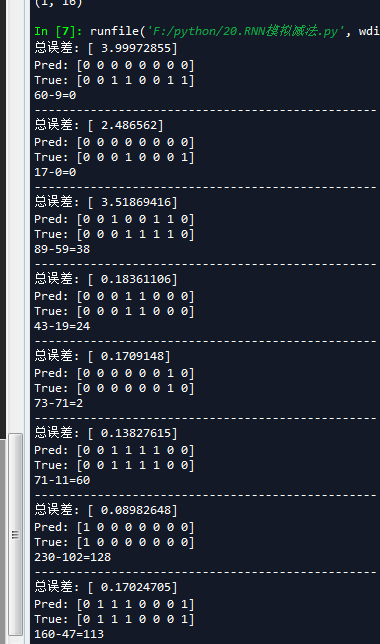
可以看到随着迭代次数的增加,计算越来越准确。
完整代码:

# -*- coding: utf-8 -*- """ Created on Sun May 6 17:33:24 2018 @author: lenovo """ ''' 裸写一个退位减法器 使用python编写简单循环神经网络拟合一个退位减法的操作,观察其反向传播过程 ''' import numpy as np import copy #规定随机数生成器的种子,可以每次得到一样的值 np.random.seed(0) ''' 一 定义基本函数 ''' def sigmoid(x): ''' 定义S型函数 args: x:输入数或list、ndarray ''' return 1/(1+np.exp(-x)) def sigmoid_output_to_derivative(output): ''' 定义sigmod函数输出的导数 args: output: output:sigmoid函数的输出 假设要计算x=5时,sigmoid函数的导数,此处就传入sigmoid(5) ''' return output*(1-output) ''' 二 建立二进制映射 定义的减法最大值限制在256以内,即8位二进制的减法,定义int与二进制之间的映射字典int2binary ''' #整数到其二进制表示的映射字典 int2binary = {} #二进制的位数 binary_dim = 8 #计算0-255的二进制表示 largest_number = pow(2,binary_dim) ''' 注意 np.array([range(largest_number)],dtype=np.uint8) 返回的是[[0,1,2,3...255]] 形状1x256 如果使用这个后面需要.T进行转置 np.array(range(largest_number),dtype=np.uint8) 返回的是[0,1,2,...255]形状为(256,) 尽量不使用这种形状不明确的 然后按行转为二进制 得到256x8 ''' binary = np.unpackbits( np.array(range(largest_number),dtype=np.uint8).reshape(256,1),axis=1) #建立int-二进制映射 for i in range(largest_number): #向字典中追加数据 int2binary[i] = binary[i] ''' 三 定义参数 隐藏层的权重synapse_0(2x16),输出层的权重synapse_1(16x1),循环节点的权重synapse_h(16x16) 这里只设置权重 忽略偏置 ''' #参数设置 learning_rate = 0.9 #学习速率 input_dim = 2 #输入节点的个数为2,减数和被减数 hidden_dim = 16 #隐藏层节点个数 output_dim = 1 #输出节点个数 n_samples = 10000 #样本个数 #初始化网络 np.random.random生成一个[0,1)之间随机浮点数或size大小浮点数组 synapse_0 = (2*np.random.random((input_dim,hidden_dim))-1)*0.05 #-0.05~0.05之间 synapse_1 = (2*np.random.random((hidden_dim,output_dim))-1)*0.05 #-0.05~0.05之间 synapse_h = (2*np.random.random((hidden_dim,hidden_dim))-1)*0.05 #-0.05~0.05之间 #用于存放反向传播的权重梯度值 synapse_0_update = np.zeros_like(synapse_0) synapse_1_update = np.zeros_like(synapse_1) synapse_h_update = np.zeros_like(synapse_h) ''' 四 准备样本数据 ''' #建立循环生成样本数据,先生成两个数a,b,如果a小于b,就交换位置,保证被减数大 for i in range(n_samples): #生成一个数字a 被减数 范围[0,256)之间的整数 a_int = np.random.randint(largest_number) #生成一个数字b 减数,b的最大值取得是largest_number/2 b_int = np.random.randint(largest_number/2) #如果生成的b>a交换 if a_int < b_int: tmp = b_int b_int = a_int a_int = tmp #二进制编码 a = int2binary[a_int] #被减数 b = int2binary[b_int] #减数 c = int2binary[a_int - b_int] #差值 ''' 五 模型初始化 ''' d = np.zeros_like(c) #存储神经网络的预测值 初始化为0 over_all_error = 0 #初始化总误差为0 layer_2_deltas = list() #存储每个时间点输出层的误差 layer_1_values = list() #存储每个时间点隐藏层的值 layer_1_values.append(np.ones(hidden_dim)*0.1) #一开始没有隐藏层(t=1),所以初始化原始值为0.1 ''' 六 正向传播 ''' #循环遍历每一个二进制位 for position in range(binary_dim): #生成输入和输出 从右向左,每次取两个输入数字的一个bit位 X = np.array([[a[binary_dim - position- 1],b[binary_dim - position - 1]]]) #正确答案 y = np.array([[c[binary_dim - position -1]]]).T #计算隐藏层输出 新的隐藏层 = 输入层 + 之前的隐藏层 layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h)) #将隐藏层保存下来,下个事件序列可以使用 layer_1_values.append(copy.deepcopy(layer_1)) #计算输出层 layer_2 = sigmoid(np.dot(layer_1,synapse_1)) #预测误差 layer_2_error = layer_2 - y #把每个时间点的误差导数都记录下来 layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2)) #总误差 over_all_error += np.abs(layer_2_error[0]) #记录每个预测的bit位 d[binary_dim - position - 1] = np.round(layer_2[0][0]) fuature_layer_1_delta = np.zeros(hidden_dim) ''' 七 反向训练 ''' for position in range(binary_dim): X = np.array([[a[position],b[position]]]) #最后一次的两个输入 layer_1 = layer_1_values[-position-1] #当前时间点的隐藏层 prev_layer_1 = layer_1_values[-position-2] #前一个时间点的隐藏层 layer_2_delta = layer_2_deltas[-position-1] #当前时间点输出导数 #通过后一个时间点的一隐藏层误差和当前时间点的输出层误差,计算当前时间点的隐藏层误差 layer_1_delta = (fuature_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T))*sigmoid_output_to_derivative(layer_1) #等完成了所有反向传播误差计算,才会更新权重矩阵,先暂时把梯度矩阵存起来 synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta) synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta) synapse_0_update += X.T.dot(layer_1_delta) fuature_layer_1_delta = layer_1_delta #完成所有反向传播之后,更新权重矩阵,并把矩阵梯度变量清0 synapse_0 -= synapse_0_update*learning_rate synapse_1 -= synapse_1_update*learning_rate synapse_h -= synapse_h_update*learning_rate synapse_0_update = 0 synapse_1_update = 0 synapse_h_update = 0 ''' 八 打印输出结果 ''' if i%800 == 0: print('总误差:',str(over_all_error)) print('Pred:',str(d)) print('True:',str(c)) out = 0 for index,x in enumerate(reversed(d)): out += x*pow(2,index) print(str(a_int) + '-' + str(b_int) + '=' + str(out)) print('-------------------------------------------------')
参考文献



 浙公网安备 33010602011771号
浙公网安备 33010602011771号