第十四节，TensorFlow中的反卷积，反池化操作以及gradients的使用

反卷积是指，通过测量输出和已知输入重构未知输入的过程。在神经网络中，反卷积过程并不具备学习的能力，仅仅是用于可视化一个已经训练好的卷积神经网络，没有学习训练的过程。反卷积有着许多特别的应用，一般可以用于信道均衡、图像恢复、语音识别、地震学、无损探伤等未知输入估计和过程辨识方面的问题。

在神经网络的研究中，反卷积更多的是充当可视化的作用，对于一个复杂的深度卷积网络，通过每层若干个卷积核的变换，我们无法知道每个卷积核关注的是什么，变换后的特征是什么样子。通过反卷积的还原，可以对这些问题有个清晰的可视化，以各层得到的特征图作为输入，进行反卷积得到反卷积结果，以验证显示各层提取到的特征图。

一 反卷积原理

反卷积可以理解为卷积操作的逆操作，这里千万不要当成反卷积操作可以复原卷积操作的输入值，反卷积并没有那个功能，它仅仅是将卷积变换过程中的步骤反向变换一次而已，通过将卷积核转置，与卷积后的结果再做一遍卷积，所以它还有一个名字叫做转置卷积。

举个例子：假如你想要查看Alexnet 的conv5提取到了什么东西，我们就用conv5的特征图后面接一个反卷积网络，然后通过：反池化、反激活、反卷积，这样的一个过程，把本来一张13*13大小的特征图(conv5大小为13*13)，放大回去，最后得到一张与原始输入图片一样大小的图片(227*227)。

虽然它不能还原出原来卷积的样子，但是在作用上有类似的效果，你可以将带有小部分缺失的信息最大化的恢复，也可以用来恢复被卷积生成后的原始输入。

反卷积的具体操作比较复杂，这里不介绍如何具体实现反卷积，在tensorflow中反卷积的是通过函数tf.nn.conv2d_transpose()来实现的：

def conv2d_transpose(value,
                     filter,
                     output_shape,
                     strides,
                     padding="SAME",
                     data_format="NHWC",
                     name=None):

具体参数说明如下：

• value:代表通过卷积操作之后的张量，一般用NHWC类型。如果是NHWC类型，形状[batch, height, width, in_channels]，如果是NCHW类型，形状为[batch, in_channels, height, width]。
• filter：代表卷积核，形状为[height, width, output_channels, in_channels]。
• output_shape：反卷积输出的张量形状，它必须是能够生成value参数的原数据的形状，如果输出形状不对，函数会报错。
• strides:代表原数据生成value时使用的步长。
• padding:代表原数据生成value时使用的填充方式，是用来检查输入形状和输出形状是否合规的。
• data_format: 'NHWC' and 'NCHW' 类型。
• name：名称。

返回反卷积后的形状，按照output_shape指定的形状。

查看该函数的实现代码，我们可以看到反卷积的操作其实是使用了gen_nn_ops.conv2d_backprop_input()函数来实现的，相当于在TensorFlow中利用了卷积操作在反向传播的处理函数中做反卷积操作，即卷积操作的反向传播就是反卷积操作。

注意：在使用反卷积的网络中，定义占位符中不能存在None，必须指定具体的数，不然会报错。

二 反卷积实例

 我们通过对模拟数据进行卷积核反卷积的操作，来比较卷积与反卷积中padding在SAME和VALID下的变化。先定义一个[1,4,4,1]的矩阵，矩阵里的元素值都为1，与滤波器大小为2x2，步长为2x2，分别使用padding为SAME和VALID两种情况生成卷积数据，然后将结果再进行反卷积运算，打印输出的结果

'''
一 反卷积实例
'''
import tensorflow as tf
import numpy as np

#模拟数据
img = tf.Variable(tf.constant(1.0,shape=[1,4,4,1]))

kernel =tf.Variable(tf.constant([1.0,0,-1,-2],shape=[2,2,1,1]))

#分别进行VALID和SAME操作
conv =  tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding='VALID')
cons =  tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding='SAME')

#VALID填充计算方式 (n - f + 1)/s向上取整
print(conv.shape)
#SAME填充计算方式 n/s向上取整
print(cons.shape)

#在进行反卷积操作
contv = tf.nn.conv2d_transpose(conv,kernel,[1,4,4,1],strides=[1,2,2,1],padding='VALID')
conts = tf.nn.conv2d_transpose(cons,kernel,[1,4,4,1],strides=[1,2,2,1],padding='SAME')

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    
    print('kernel:\n',sess.run(kernel))
    print('conv:\n',sess.run(conv))
    print('cons:\n',sess.run(cons))
    print('contv:\n',sess.run(contv))
    print('conts:\n',sess.run(conts))

我们可以把padding为VALID方式时的卷积核反卷积操作绘制出来，如下图：

三 反池化原理

反池化属于池化的逆操作，是无法通过池化的结果还原出全部的原始数据，因此池化的过程只保留主要信息，舍去部分信息。如果想从池化后的这些主要信息恢复出全部信息，由于存在着信息缺失，这时只能通过补位来实现最大程度的信息完整。

池化层常用的有最大池化和平均池化，其反池化也需要与其对应。

• 平均池化比较简单。首先还原成原来的大小，然后将池化结果中的每个值都填入其对应于原始数据区域中的相应位置即可。如下图：
• 

   

• 最大池化的反池化会复杂一些。要求在池化过程中记录最大激活池的坐标位置，然后在反池化时，只把池化过程中最大激活值所在位置坐标的值激活，其它位置为0.当然，这个过程只是一种近似，因为在池化的过程中，除了最大值所在的位置，其他的值也是不为0的。如下图：
•  

四 反池化实例

TensorFlow中目前还没有反池化操作的函数。对于最大池化层，也不支持输出最大激活值得位置，但是同样有个池化的反向传播函数tf.nn.max_pool_with_argmax()。该函数可以找出位置，需要开发者利用这个函数做一些改动，自己封装一个最大池化操作，然后再根据mask写出反池化函数。

'''
二 反池化操作
'''

def max_pool_with_argmax(net,stride):
    '''
    重定义一个最大池化函数，返回最大池化结果以及每个最大值的位置(是个索引，形状和池化结果一致)
    
    args:
        net:输入数据 形状为[batch,in_height,in_width,in_channels]
        stride：步长，是一个int32类型，注意在最大池化操作中我们设置窗口大小和步长大小是一样的
    '''
    #使用mask保存每个最大值的位置 这个函数只支持GPU操作
    _, mask = tf.nn.max_pool_with_argmax( net,ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1],padding='SAME')
    #将反向传播的mask梯度计算停止
    mask = tf.stop_gradient(mask)
    #计算最大池化操作
    net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1],strides=[1, stride, stride, 1], padding='SAME') 
    #将池化结果和mask返回
    return net,mask



def un_max_pool(net,mask,stride):
    '''
    定义一个反最大池化的函数，找到mask最大的索引，将max的值填到指定位置
    args:
        net:最大池化后的输出，形状为[batch, height, width, in_channels]
        mask：位置索引组数组，形状和net一样
        stride:步长，是一个int32类型，这里就是max_pool_with_argmax传入的stride参数
    '''
    ksize = [1, stride, stride, 1]
    input_shape = net.get_shape().as_list()
    #  calculation new shape
    output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3])
    # calculation indices for batch, height, width and feature maps
    one_like_mask = tf.ones_like(mask)
    batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1])
    b = one_like_mask * batch_range
    y = mask // (output_shape[2] * output_shape[3])
    x = mask % (output_shape[2] * output_shape[3]) // output_shape[3]
    feature_range = tf.range(output_shape[3], dtype=tf.int64)
    f = one_like_mask * feature_range
    # transpose indices & reshape update values to one dimension
    updates_size = tf.size(net)
    indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size]))
    values = tf.reshape(net, [updates_size])
    ret = tf.scatter_nd(indices, values, output_shape)
    return ret

#定义一个形状为4x4x2的张量
img = tf.constant([
            [[0.0,4.0],[0.0,4.0],[0.0,4.0],[0.0,4.0]],
            [[1.0,5.0],[1.0,5.0],[1.0,5.0],[1.0,5.0]],
            [[2.0,6.0],[2.0,6.0],[2.0,6.0],[2.0,6.0]],
            [[3.0,7.0],[3.0,7.0],[3.0,7.0],[3.0,7.0]],
        ])
    
img = tf.reshape(img,[1,4,4,2])
#最大池化操作
pooling1 = tf.nn.max_pool(img,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
#带有最大值位置的最大池化操作
pooling2,mask = max_pool_with_argmax(img,2)
#反最大池化
img2 = un_max_pool(pooling2,mask,2)
with tf.Session() as sess:
    print('image:')
    image = sess.run(img)
    print(image)
    
    #默认的最大池化输出
    result = sess.run(pooling1)
    print('max_pool:\n',result)
    
    #带有最大值位置的最大池化输出
    result,mask2 = sess.run([pooling2,mask])
    print('max_pool_with_argmax:\n',result,mask2)
    
    #反最大池化输出
    result = sess.run(img2)
    print('un_max_pool',result)

这里我们自己定义了两个函数，一个是带有最大值位置的最大池化函数，一个反最大池化函数，程序运行后，我们应该可以看到自己定义的最大池化与原来的版本输出是一样的，由于tf.nn.max_pool_with_argmax()函数只支持GPU操作，不能在CPU机器上运行，所以我没法运行这段程序。mask的值是将整个数组flat后的索引，并保持与池化结果一致的shape。

五 偏导计算

在反向传播的过程中，神经网络需要对每个代价函数对应的学习参数求偏导，计算出的这个值叫做梯度，用来乘以学习率然后更新学习参数使用的。它是通过tf.gradients()函数来实现的，这个函数的第一个参数为需要求导的公式，第二个参数为指定公式中的哪个变量来求偏导。如果对一个不存在的变量求偏导，会返回None。

'''
三 偏导计算
'''    
w1 = tf.Variable([[1,2]])       #1x2
w2 = tf.Variable([[3,4]])       #1x2

y = tf.matmul(w1,[[9],[10]])    #2x1
#求w1的梯度
grads = tf.gradients(y,w1)      #1x2

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    gradval = sess.run(grads)
    print(gradval)
    

可以看到我们计算得到的结果为[[9,10]]，形状为1x2，即[[9],[10]]的转置。至于为什么是其转置，你需要了解一下矩阵如何求偏导的知识。

import numpy as np
x = np.array([[9,10]])
print(x.shape)

x = np.array([[9],[10]])
print(x.shape)

tf.gradients()函数还可以同时对多个子式求关于多个变量的偏导：

tf.reset_default_graph()
w1 = tf.get_variable('w1',shape=[2])
w2 = tf.get_variable('w2',shape=[2])

w3 = tf.get_variable('w3',shape=[2])
w4 = tf.get_variable('w4',shape=[2])

y1 = w1 + w2 + w3
y2 = w3 + w4

gradients = tf.gradients([y1,y2],[w1,w2,w3,w4],grad_ys=[tf.convert_to_tensor([1.,2.]),tf.convert_to_tensor([3.,4.])])
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    gradval = sess.run(gradients)
    print(gradval)

上面的程序有两个op，4个参数，演示了使用tf.gradients()函数同时为两个式子4个参数求梯度。

这里使用了tf.gradients()函数的第三个参数，即给定公式结果的值，来求参数梯度，这里相当于y1为[1.,2.],y2为[3.,4.]。对于y1来讲，求关于w1的梯度时，会认为w2和w3为常数，所以w2,w3的导数为0，即w1的梯度就为[1.,2.]。同理可以得出w2,w3均为[1.,2.]，接着求y2的梯度，得到w3和w4均为[3.,4.]。然后将两个式子中的w3结果加起来，所以w3就为[4.,6.]。(这一块我也没有懂，一脸懵逼)

六 梯度停止

对于反向传播过程中某种情况需要停止梯度的运算时，在TensorFlow中提供了一个tf.stop_gradient()函数，被它定义过得节点将没有梯度运算的功能。

'''
四 梯度停止
'''
w1 = tf.Variable(2.0)
w2 = tf.Variable(2.0)

a = tf.multiply(w1, 3.0)
#停止a节点梯度运算的功能
a_stoped = tf.stop_gradient(a)

b = tf.multiply(a_stoped, w2)
gradients = tf.gradients(b, xs=[w1, w2])
print(gradients)

可见，一个节点被 stop之后，这个节点上的梯度，就无法再向前BP了。由于w1变量的梯度只能来自a节点，由于停止了1节点梯度运算的功能，所以，计算梯度返回的是None。

a = tf.Variable(1.0)
b = tf.Variable(1.0)

c = tf.add(a, b)
#停止c节点梯度运算的功能
c_stoped = tf.stop_gradient(c)
d = tf.add(a, b)
e = tf.add(c_stoped, d)

gradients = tf.gradients(e, xs=[a, b])

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    print(sess.run(gradients))

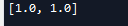
虽然 c节点被stop了，但是a，b还有从d传回的梯度，所以还是可以输出梯度值的。

完整代码：

# -*- coding: utf-8 -*-
"""
Created on Fri May  4 17:04:22 2018

@author: zy
"""

'''
一 反卷积实例
'''
import tensorflow as tf
import numpy as np

#模拟数据
img = tf.Variable(tf.constant(1.0,shape=[1,4,4,1]))

kernel =tf.Variable(tf.constant([1.0,0,-1,-2],shape=[2,2,1,1]))

#分别进行VALID和SAME操作
conv =  tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding='VALID')
cons =  tf.nn.conv2d(img,kernel,strides=[1,2,2,1],padding='SAME')

#VALID填充计算方式 (n - f + 1)/s向上取整
print(conv.shape)
#SAME填充计算方式 n/s向上取整
print(cons.shape)

#在进行反卷积操作
contv = tf.nn.conv2d_transpose(conv,kernel,[1,4,4,1],strides=[1,2,2,1],padding='VALID')
conts = tf.nn.conv2d_transpose(cons,kernel,[1,4,4,1],strides=[1,2,2,1],padding='SAME')

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    
    print('kernel:\n',sess.run(kernel))
    print('conv:\n',sess.run(conv))
    print('cons:\n',sess.run(cons))
    print('contv:\n',sess.run(contv))
    print('conts:\n',sess.run(conts))



'''
二 反池化操作
'''

def max_pool_with_argmax(net,stride):
    '''
    重定义一个最大池化函数，返回最大池化结果以及每个最大值的位置(是个索引，形状和池化结果一致)
    
    args:
        net:输入数据 形状为[batch,in_height,in_width,in_channels]
        stride：步长，是一个int32类型，注意在最大池化操作中我们设置窗口大小和步长大小是一样的
    '''
    #使用mask保存每个最大值的位置 这个函数只支持GPU操作
    _, mask = tf.nn.max_pool_with_argmax( net,ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1],padding='SAME')
    #将反向传播的mask梯度计算停止
    mask = tf.stop_gradient(mask)
    #计算最大池化操作
    net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1],strides=[1, stride, stride, 1], padding='SAME') 
    #将池化结果和mask返回
    return net,mask



def un_max_pool(net,mask,stride):
    '''
    定义一个反最大池化的函数，找到mask最大的索引，将max的值填到指定位置
    args:
        net:最大池化后的输出，形状为[batch, height, width, in_channels]
        mask：位置索引组数组，形状和net一样
        stride:步长，是一个int32类型，这里就是max_pool_with_argmax传入的stride参数
    '''
    ksize = [1, stride, stride, 1]
    input_shape = net.get_shape().as_list()
    #  calculation new shape
    output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3])
    # calculation indices for batch, height, width and feature maps
    one_like_mask = tf.ones_like(mask)
    batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1])
    b = one_like_mask * batch_range
    y = mask // (output_shape[2] * output_shape[3])
    x = mask % (output_shape[2] * output_shape[3]) // output_shape[3]
    feature_range = tf.range(output_shape[3], dtype=tf.int64)
    f = one_like_mask * feature_range
    # transpose indices & reshape update values to one dimension
    updates_size = tf.size(net)
    indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size]))
    values = tf.reshape(net, [updates_size])
    ret = tf.scatter_nd(indices, values, output_shape)
    return ret

'''
#定义一个形状为4x4x2的张量
img = tf.constant([
            [[0.0,4.0],[0.0,4.0],[0.0,4.0],[0.0,4.0]],
            [[1.0,5.0],[1.0,5.0],[1.0,5.0],[1.0,5.0]],
            [[2.0,6.0],[2.0,6.0],[2.0,6.0],[2.0,6.0]],
            [[3.0,7.0],[3.0,7.0],[3.0,7.0],[3.0,7.0]],
        ])
    
img = tf.reshape(img,[1,4,4,2])
#最大池化操作
pooling1 = tf.nn.max_pool(img,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
#带有最大值位置的最大池化操作
pooling2,mask = max_pool_with_argmax(img,2)
#反最大池化
img2 = un_max_pool(pooling2,mask,2)
with tf.Session() as sess:
    print('image:')
    image = sess.run(img)
    print(image)
    
    #默认的最大池化输出
    result = sess.run(pooling1)
    print('max_pool:\n',result)
    
    #带有最大值位置的最大池化输出
    result,mask2 = sess.run([pooling2,mask])
    print('max_pool_with_argmax:\n',result,mask2)
    
    #反最大池化输出
    result = sess.run(img2)
    print('un_max_pool',result)
'''


'''
三 偏导计算
'''    
w1 = tf.Variable([[1,2]])       #1x2
w2 = tf.Variable([[3,4]])       #1x2

y = tf.matmul(w1,[[9],[10]])    #2x1
#求w1的梯度
grads = tf.gradients(y,w1)      #1x2

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    gradval = sess.run(grads)
    print(gradval)
    

tf.reset_default_graph()
w1 = tf.get_variable('w1',shape=[2])
w2 = tf.get_variable('w2',shape=[2])

w3 = tf.get_variable('w3',shape=[2])
w4 = tf.get_variable('w4',shape=[2])

y1 = w1 + w2 + w3
y2 = w3 + w4

gradients = tf.gradients([y1,y2],[w1,w2,w3,w4],grad_ys=[tf.convert_to_tensor([1.,2.]),tf.convert_to_tensor([3.,4.])])
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    gradval = sess.run(gradients)
    print(gradval)
    

'''
四 梯度停止
'''
w1 = tf.Variable(2.0)
w2 = tf.Variable(2.0)

a = tf.multiply(w1, 3.0)
#停止a节点梯度运算的功能
a_stoped = tf.stop_gradient(a)

b = tf.multiply(a_stoped, w2)
gradients = tf.gradients(b, xs=[w1, w2])
print(gradients)


a = tf.Variable(1.0)
b = tf.Variable(1.0)

c = tf.add(a, b)
#停止c节点梯度运算的功能
c_stoped = tf.stop_gradient(c)
d = tf.add(a, b)
e = tf.add(c_stoped, d)

gradients = tf.gradients(e, xs=[a, b])

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    print(sess.run(gradients))

参考文章

[1]用反卷积（Deconvnet）可视化理解卷积神经网络

[2]tensorflow学习笔记（三十）：tf.gradients 与 tf.stop_gradient() 与 高阶导数

[3]卷积神经网络中卷积、反卷积、池化解析