第十节,利用隐藏层解决非线性问题-异或问题
多层神经网络非常好理解,就是在输入和输出中间多加一些层,每一层可以加多个神经元。下面的例子是通过加入一个隐藏层后对异或数据进行分类。
一 异或数据集
所谓的"异或数据"是来源于异或操作,可以绘制在直角坐标系中,如下图所示:

我们可以看到这张图很难通过一个直线把这两类数据风格开来,但是我们可以通过类似支持向量机中核函数一样的函数把数据映射到高维空间,然后通过线性分类的方法把数据分类。在输入层和输出层之间加一层隐藏层,就是起到核函数的作用。
生成数据集的代码如下:
''' 生成模拟数据集 ''' train_x = np.array([[0,0],[0,1],[1,0],[1,1]],dtype=np.float32) #非one_hot编码 #train_y = np.array([[0],[1],[1],[0]],dtype = np.float32) #输出层节点个数 #n_label = 1 #one_hot编码 train_y = np.array([[1, 0], [0, 1], [0, 1], [1, 0]],dtype = np.float32) #输出层节点个数 n_label = 2
二 定义参数
''' 定义变量 ''' #学习率 learning_rate = 1e-4 #输入层节点个数 n_input = 2 #隐藏层节点个数 n_hidden = 2 input_x = tf.placeholder(tf.float32,[None,n_input]) input_y = tf.placeholder(tf.float32,[None,n_label]) ''' 定义学习参数 h1 代表隐藏层 h2 代表输出层 ''' weights = { 'h1':tf.Variable(tf.truncated_normal(shape=[n_input,n_hidden],stddev = 0.01)), #方差0.01 'h2':tf.Variable(tf.truncated_normal(shape=[n_hidden,n_label],stddev=0.01)) } biases = { 'h1':tf.Variable(tf.zeros([n_hidden])), 'h2':tf.Variable(tf.zeros([n_label])) }
三 定义网络结构
''' 定义网络模型 ''' #隐藏层 layer_1 = tf.nn.relu(tf.add(tf.matmul(input_x,weights['h1']),biases['h1'])) #1 softmax 方法 y_pred = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['h2']),biases['h2'])) loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits( labels=input_y,logits=y_pred)) #2 tanh方法+平方差#输出层 #y_pred = tf.nn.tanh(tf.add(tf.matmul(layer_1,weights['h2']),biases['h2'])) #定义代价函数 二次代价函数 #loss = tf.reduce_mean((y_pred - input_y)**2) train = tf.train.AdamOptimizer(learning_rate).minimize(loss)
四 开始训练
''' 开始训练 ''' training_epochs = 100000 sess = tf.InteractiveSession() #初始化 sess.run(tf.global_variables_initializer()) for epoch in range(training_epochs): _,lo = sess.run([train,loss],feed_dict={input_x:train_x,input_y:train_y}) if epoch % 10000 == 0: print(lo) #计算预测值 print(sess.run(y_pred,feed_dict={input_x:train_x})) #查看隐藏层的输出 print(sess.run(layer_1,feed_dict={input_x:train_x}))
运行结果如下:
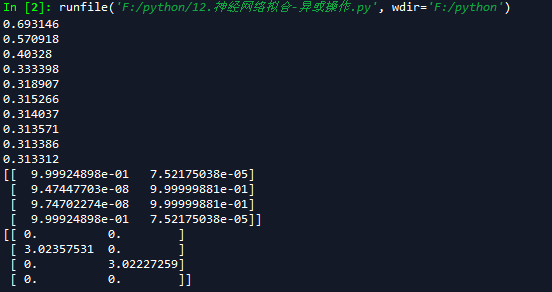
上面输出了两个数组,第一个数组是一个4行两列的输出,如果我们采用四舍五入取值,我们会发现,和我们的输入train_y值完全吻合。
第二个数组也是一个4行2列的数组,我们可以看到这4个元素是线性可分的,也就是说隐藏层把输入数据从输入空间映射到了特征空间中,将非线性问题变换成了线性分类问题。
如果你运行的结果并不能正确分类,可能你需要调整你的学习率和迭代周期,因为在训练过程中可能陷入局部最优。
全部代码:

# -*- coding: utf-8 -*- """ Created on Wed Apr 25 20:41:45 2018 @author: zy """ ''' 非线性分类问题:就是用直线分不开的问题 我们可以使用隐藏层解决非线性问题 ''' ''' 使用带隐藏层的神经网络拟合异或操作 input1 input2 output 0 0 0 0 1 1 1 0 1 1 1 0 ''' import tensorflow as tf import numpy as np ''' 生成模拟数据集 ''' train_x = np.array([[0,0],[0,1],[1,0],[1,1]],dtype=np.float32) #非one_hot编码 #train_y = np.array([[0],[1],[1],[0]],dtype = np.float32) #输出层节点个数 #n_label = 1 #one_hot编码 train_y = np.array([[1, 0], [0, 1], [0, 1], [1, 0]],dtype = np.float32) #输出层节点个数 n_label = 2 ''' 定义变量 ''' #学习率 learning_rate = 1e-4 #输入层节点个数 n_input = 2 #隐藏层节点个数 n_hidden = 2 input_x = tf.placeholder(tf.float32,[None,n_input]) input_y = tf.placeholder(tf.float32,[None,n_label]) ''' 定义学习参数 h1 代表隐藏层 h2 代表输出层 ''' weights = { 'h1':tf.Variable(tf.truncated_normal(shape=[n_input,n_hidden],stddev = 0.01)), #方差0.1 'h2':tf.Variable(tf.truncated_normal(shape=[n_hidden,n_label],stddev=0.01)) } biases = { 'h1':tf.Variable(tf.zeros([n_hidden])), 'h2':tf.Variable(tf.zeros([n_label])) } ''' 定义网络模型 ''' #隐藏层 layer_1 = tf.nn.relu(tf.add(tf.matmul(input_x,weights['h1']),biases['h1'])) #1 softmax 方法 y_pred = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['h2']),biases['h2'])) loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits( labels=input_y,logits=y_pred)) #2 tanh方法+平方差#输出层 #y_pred = tf.nn.tanh(tf.add(tf.matmul(layer_1,weights['h2']),biases['h2'])) #定义代价函数 二次代价函数 #loss = tf.reduce_mean((y_pred - input_y)**2) train = tf.train.AdamOptimizer(learning_rate).minimize(loss) ''' 开始训练 ''' training_epochs = 100000 sess = tf.InteractiveSession() #初始化 sess.run(tf.global_variables_initializer()) for epoch in range(training_epochs): _,lo = sess.run([train,loss],feed_dict={input_x:train_x,input_y:train_y}) if epoch % 10000 == 0: print(lo) #计算预测值 print(sess.run(y_pred,feed_dict={input_x:train_x})) #查看隐藏层的输出 print(sess.run(layer_1,feed_dict={input_x:train_x}))



 浙公网安备 33010602011771号
浙公网安备 33010602011771号