02 复杂度分析(下):浅析最好、最坏、平均、均摊时间复杂度
一、最好、最坏情况时间复杂度
最好情况时间复杂度就是,在最理想的情况下执行这段代码的时间复杂度。
最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。
二、平均情况时间复杂度
// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
要查找的变量 x 在数组中的位置,有 n+1 种情况:在数组 0 ~ n-1 位置中和不在数组中。我们把每种情况下,查找需要遍历的元素个数累加起来,然后再除以 n+1,就可以得到需要遍历的元素个数的平均值,即:

所以,得到的平均时间复杂度就是 O(n)。
但是这 n+1 种情况,出现的概率并不是一样的。我们知道,要查找的变量 x ,要么在数组里,要么就不在数组里。我们假设在数组中与不在数组中的概率都为1/2。另外,要查找的数据出现在 0 ~ n-1 这 n 个位置的概率也是一样的,为 1/n。所以,根据概率乘法法则,要查找的数据出现在 0 ~ n-1 中任意位置的概率就是 1/(2n)。那么平均时间复杂度的计算过程就变成了这样:
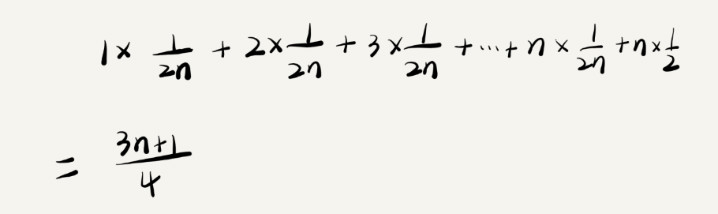
这个值就是概率论中的加权平均值也叫作期望值,所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。
引入概率之后,前面那段代码的加权平均值为 (3n+1)/4。用大 O 表示法来表示去掉系数和常量,这段代码的加权平均时间复杂度仍然是 O(n)。
三、均摊时间复杂度
// array表示一个长度为n的数组
// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;
void insert(int val) {
if (count == array.length) {
int sum = 0;
for (int i = 0; i < array.length; ++i) {
sum = sum + array[i];
}
array[0] = sum;
count = 1;
}
array[count] = val;
++count;
}
上面这段代码的最好情况时间复杂度为 O(1),最坏情况时间复杂度为 O(n),平均时间复杂度为 O(1)。
假设数组的长度是 n,根据数据插入的位置的不同,我们可以分为 n 种情况,每种情况的时间复杂度是 O(1)。除此之外,还有一种“额外”的情况,就是在数组没有空闲空间时插入一个数据,这个时候的时间复杂度是 O(n)。而且,这 n+1 种情况发生的概率一样,都是 1/(n+1)。所以,根据加权平均的计算方法,我们求得的平均时间复杂度就是:




