LCA最近公共祖先算法
LCA最近公共祖先
LCA是指在有根树中，找出某两个节点\(u\)和\(v\)的最近公共祖先，即找到一个节点，同时是\(u\)和\(v\)的公共祖先，并且深度尽可能大
模板题目链接：https://www.luogu.com.cn/problem/P3379
朴素算法
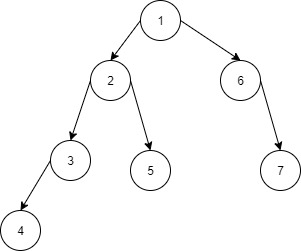
比如对于下面这样一个树，求LCA的过程，大体如下，首先我们先求出标号为4的节点的所有父节点，然后在对标号为5的节点不断向上求父节点，判断是否在4的父节点中，如果是就求出了就求出了公共祖先，如果树的深度很大，时间复杂度就是\(O(n + m)\)
倍增法
我们可以考虑，如果两个节点同事向上跳，直到相遇，相遇的点就是他们的LCA。但是如果树的深度很大，就需要跳很久，时间复杂度就是\(O(n*m)\)。采用倍增法来优化。
首先记录下每个节点的父节点和各个祖先节点，使用一个\(f[N][30]\)数组用来表示节点\(x\)的第\(i + 1\)位祖先，也就是说\(x\)的父亲节点是\(f[x][0]\)，这样我们在更新的时候可以得到一个递推式，\(f[x][i] = f[f[i][i-1]][i-1]\)，就可以预处理处每个节点的祖先
在向上跳的时候，首先让\(x\)和\(y\)处于同一层，让深度更深的向上跳，然后两个在一起跳，知道两个节点有了同一个父节点。当然我们可以再两个节点处于同一层的时候，判断是否汇合如果汇合，就返回
时间复杂度
\(O(mlog(n))\)
实现代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 500010, M = N * 2;
int n, m, root;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][26];
int q[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void bfs(int root) {
memset(depth, 0x3f, sizeof depth);
depth[0] = 0, depth[root] = 1;
int hh = 0, tt = 0;
q[0] = root;
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (depth[j] > depth[t] + 1) {
depth[j] = depth[t] + 1;
q[++tt] = j;
fa[j][0] = t;
for (int k = 1; k <= 25; k++)
fa[j][k] = fa[fa[j][k - 1]][k - 1];
}
}
}
}
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int k = 25; k >= 0; k--)
if (depth[fa[a][k]] >= depth[b])
a = fa[a][k];
if (a == b) return a;
for (int k = 25; k >= 0; k--)
if (fa[a][k] != fa[b][k]) {
a = fa[a][k];
b = fa[b][k];
}
return fa[a][0];
}
int main() {
scanf("%d%d%d", &n, &m, &root);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i++) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
bfs(root);
while (m--) {
int a, b;
scanf("%d%d", &a, &b);
int p = lca(a, b);
printf("%d\n", p);
}
return 0;
}
Tarjan
可以看出倍增的做法是强制在线算法，必须针对每一个问题去单独运行lca。Tarjan是强制离线算法，每次将结果计算好，然后直接查询即可。
tarjan算法的流程如下：
- 从根节点开始
- 遍历该点\(u\)的所有子节点\(v\)，并标记这些子节点\(v\)已经被访问过了
- 如果\(u\)还有子节点，就重复步骤2
- 合并\(v\)到\(u\)上
- 寻找与当前点\(u\)有询问关系的点\(v\)
- 如果\(v\)已经被访问过了，则可以确定\(u\)和\(v\)的最近公共祖先为\(v\)被合并到父亲节点\(a\)
实现代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 500010, M = 2 * N;
int n, m, root;
int h[N], e[M], ne[M], idx;
int p[N];
int res[M];
int st[N];
int dist[N];
// first 存查询的另外一个点，second存查询编号
vector <PII> query[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int find(int x) {
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
void tarjan(int u) {
st[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!st[j]) {
tarjan(j);
p[j] = u;
}
}
for (auto item : query[u]) {
int y = item.first, id = item.second;
if (st[y] == 2) {
int anc = find(y);
res[id] = anc;
}
}
st[u] = 2;
}
int main() {
scanf("%d%d%d", &n, &m, &root);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i++) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d%d", &a, &b);
if (a != b) {
query[a].push_back({b, i});
query[b].push_back({a, i});
}
}
for (int i = 1; i <= n; i++) p[i] = i;
tarjan(root);
for (int i = 0; i < m; i++) printf("%d\n", res[i]);
return 0;
}
