| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 课程班级 |
| 这个作业要求链接 | 作业要求 |
| 我的课程学习目标 | 1、掌握软件项目个人开发流程并且会自己编制自己的PSP 2、掌握Github发布软件项目的操作方法 3、能通过本次博客,了解背包{0-1}问题,以及动态规划算法和回溯算法 |
| 这个作业在哪些方面帮助我实现学习目标 | 1、通过展示自己的PSP,让我掌握了PSP的绘制流程 2、通过查找资料和网上的学习视频,让我对背包问题及其两个算法有了一定的认识 |
| 项目Github的仓库链接地址 | https://github.com/1911296608/shiyan-2#shiyan-2 |
| PSP 各个阶段 | 自己预估的时间(小时) | 实际的记录(小时) |
|---|---|---|
| 计划 | 1 | 2 |
| . 明确需求和其他因素,估计以下的各个任务需要多少时间 | 1 | 2 |
| 开发 | 预估时间 | 实际开发时间 |
| . 需求分析 | 5 | 8 |
| . 生成设计文档 | 3 | 4 |
| . 设计复审 | 3 | 5 |
| . 代码规范 | 3 | 3 |
| . 具体设计 | 5 | - |
| . 具体编码 | 15 | - |
| . 代码复审 | 2 | - |
| . 测试(自我测试,修改代码,提交修改) | 6 | - |
| 报告 | 1 | - |
| . 测试报告 | 3 | - |
| . 计算工作量 | 1 | 2 |
| . 事后总结, 并提出改进计划 | 2 | - |
| 总共花费的时间 (小时) | 50 | - |
psp有如下特点:
* 不仅局限于某一软件技术,而是着眼于软件开发流程
* 不依赖于考试,而主要靠工程是自己收集数据,然后分析提高
* 在小型初创的团队中很难找到高质量的项目需求,这意味着给程序员的收入质量不高
* PSP依赖于数据,需要工程师输入数据
* PSP的目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度
-
任务三
-
背包问题(KP):{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大。0-1背包:每类物品最多只能装一次。
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法 -
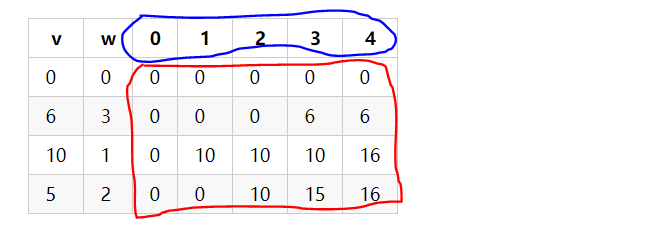
动态规划算法解决D{0-1}: 在给定了物品的重量(容量)和价值的情况下,当装入物品时,查看背包的最大容量是否大于当前物品的容量,如果装得下当前物品,则在给当前物品预留了相应空间的情况下,前n-1个物品的最佳组合加上当前物品的价值就是总价值。当前的价值与前面的价值作比较,选取较大的为最佳价值。如果没有装下当前物品,则前n个物品的最佳组合和前n-1个物品的最佳组合的价值是一样的。如下图所示。(蓝色部分为背包的最大承受量,红色的为最大价值)
![]()
-
回溯算法解决D{0-1}:回溯算法简单来说就是查看背包里装入了哪些物品使得背包的价值最大化。从表的右下角开始回溯(即16的位置),如果发现前n个物品最佳组合的价值和前n-1个物品最佳组合的价值一样,说明第n个物品没有被装入,否则第n个物品装入。
-
1、需求分析
-
能正确得读入数据
-
能够绘制出散点图
-
利用动态规划求最优值的方法得到背包的最大价值,然后利用回溯算法求得背包里都装了哪些物品。
2、功能设计
基本功能如下:
-
可正确读入实验数据文件的有效D{0-1}KP数据;
-
能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
-
能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
-
用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
-
任意一组D{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
3、设计实现
利用动态规划算法和回溯算法来实现{0-1}背包问题,可以用一个二维数组来记录背包的状态。假设用value[N][V]来存储中间状态值,value[i][j]表示前i件物品能装入容量为j的背包中的物品价值总和的最大值,则我们最终只需求知value[i=N][j=V]的值。
1) 若w[i]>j,则第i件物品肯定不能装入容量为j的背包,此时value[i][j]=value[i-1][j]
2) 若w[i]<=j,则首先明确的是这件物品是可以装入容量为j的背包的,那么如果我们将该物品装入,则有
value[i][j]=value[i-1][j-w[i]]+v[i]
故:状态转移方程为:
//如果容量为j的背包放得下第i个物体
if(j >= w[i])
{
//两种选择:放与不放第i个物体,策略:哪个使价值最大就选用哪种策略
value[i][j] = max(value[i - 1][j - w[i]] + v[i], value[i - 1][j]);
}
else
{
//放不下,只能选择不放第i个物体
value[i][j] = value[i - 1][j];
}
4、代码片段
(1)、动态规划
def bag(n, c, w, v):
"""
测试数据:
n 物品的数量,
c 书包能承受的重量,
w 每个物品的重量,
v 每个物品的价值
"""
# 置零,表示初始状态
value = [[0 for j in range(c + 1)] for i in range(n + 1)]
for i in range(1, n + 1):
for j in range(1, c + 1):
value[i][j] = value[i - 1][j]
# 背包总容量够放当前物体,遍历前一个状态考虑是否置换
if j >= w[i - 1] and value[i][j] < value[i - 1][j - w[i - 1]] + v[i - 1]:
value[i][j] = value[i - 1][j - w[i - 1]] + v[i - 1]
for x in value:
print(x)
return value
(2)、回溯算法
def show(n, c, w, value):
print('最大价值为:', value[n][c])
x = [False for i in range(n)]
j = c
for i in range(n, 0, -1):
if value[i][j] > value[i - 1][j]:
x[i - 1] = True
j -= w[i - 1]
print('背包中所装物品为:')
for i in range(n):
if x[i]:
print('第', i+1, '个,', end='')



 浙公网安备 33010602011771号
浙公网安备 33010602011771号